Понятие о позиционных системах счисления
Под системой счисления понимается способ представления любого числа посредством некоторого алфавита символов, называемых цифрами. Существуют различные системы счисления.
Римская система счисления является примером очень сложного способа записи чисел и имеет громоздкие правила арифметических действий. Число 35 в этой системе счисления будет записываться: ХХХУ. Такая система счисления называется непозиционной, так как цифрыздесь всегда имеют одно и то же значение независимо от того,на каком месте они стоят (Х в римской системе счисления всегда обозначает десяток).
Система счисления называется позиционной, если одна и та же цифра имеет различные значения, определяемые позицией цифры в последовательности цифр, изображающей число. Эти значения меняются в зависимости от позиции, занимаемой цифрой, по некоторому закону. Примером такой системы счисления является десятичная система, используемая в повседневной жизни. В числе двести двадцать два – 222 крайняя справа двойка обозначает две единицы, в середине - два десятка, крайняя слева - две сотни.
Количество Pразличных цифр, употребляемых в позиционной системе, называется её основанием. Эти цифрыобозначают Pцелых чиселот 0 до P -1. В десятичной системеиспользуются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, следовательно, эта система имеет основанием число десять.
В общем случае в позиционной системе с основанием Pлюбоечисло X может быть представлено в виде полиномаот основания P:
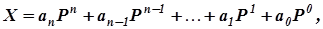 (1)
(1)
где в качестве коэффициентов  могут стоятьлюбые изP цифр, используемых в системе счисления.
могут стоятьлюбые изP цифр, используемых в системе счисления.
Принято представлять числа в виде последовательностисоответствующих выражению (1) цифр:

В этой последовательности запятая отделяет целую часть числа от дробной (коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях).Запятая опускается, если нет отрицательныхстепеней. Позиции цифр,отсчитываемые от запятой, называют разрядами. В позиционной системе счисления значение каждого разряда больше значения соседнего справа разряда в число раз, равное основанию системы P.
С учетом сказанного, в десятичной системесчисления запись6097.108 означает число:
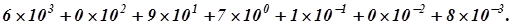
В цифровой автоматике и вычислительных машинах применяют позиционные системысчисления с недесятичным основанием: двоичную, восьмеричную и шестнадцатеричную. В дальнейшем дляобозначения используемой системы счисления будем заключать число в скобки и в индексе указывать основание системы счисления.
1.1.1. Двоичная система счисления
В двоичной системе счисления используются только две "двоичные" цифры: 0 и 1. Любое число в этой системе может быть представлено последовательностью двоичных цифр, что согласно (I) соответствует сумме степеней числа 2, взятых с коэффициентами, равными 0 или 1. Например:
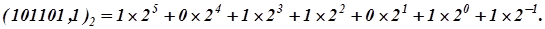
Вычисление этой суммы в десятичной системе счисления даёт десятичное значение числа 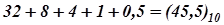 .
.
Применение двоичной системы счисления создает большие удобства при проектировании цифровых систем управления, обработки и передачи информации, так как для представления разряда двоичного числа может быть использован любой простой элемент, имевший всего два устойчивых состояния, например реле или триггерные схемы. Другим важным достоинством двоичной системы является простота двоичной арифметики, двоичные числа часто встречаются в технической литературе и могут использоваться в языках высокого уровня, таких, как «Си», «Паскаль» и т.д. Иногда для их отличия от чисел, представленных в других системах счисления, после цифр ставится буква В (от английского слова Binary). Например:
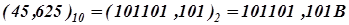
При программировании микропроцессоров и микроЭВМ часто возникает необходимость писать большие массивы двоичных чисел, но большое количество разрядов и однообразие символов служат источником ошибок программистов, поэтому для записи двоичных чисел широко применяются восьмеричная и шестнадцатеричная системы счисления. Основания этих систем кратны основанию двоичной системы счисления, что обеспечивает удобство преобразования из одной системы счисления в другую. Обычно это выполняется для целых чисел, поэтому дроби рассматривать в дальнейшем не будем.
1.1.2. Восьмеричная система счисления
В восьмеричной системе счисления используются восемь цифр: 0, 1, 2, 3, 4. 5, 6, 7. Любое число в восьмеричной системе представляется последовательностью этих цифр. Восьмеричное число также может быть представлено полиномом (1) с разложением по степеням основания 8. Например:

1.1.3. Шестнадцатеричная система счисления
В шестнадцатеричной системе для изображения чисел используют 16 знаков, которые изображаются десятью десятичными цифрами и шестью латинскими буквами: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A , B, С, D, E, F. Существуют и другие формы записи шестнадцатеричных цифр, но такая используется чаще. В этой форме - буквы используются для обозначения цифр, больших 9: А соответствует десятичному числу 10, В -десятичному числу 11, С - 12, D - 13, E - 14, F - 15. В шестнадцатеричной системе счисления любое число записывается последовательностью шестнадцатеричных цифр, и оно тоже может быть представлено полиномом ( 1) с разложением по степеням основания 16. Вычисление этого полинома в десятичной системе счисления позволяет получить десятичное значение данного числа. Например:

Для того чтобы отличать восьмеричные и шестнадцатеричные числа от записи чисел в других системах счисления, иногда используют буквенное обозначение. В конце восьмеричного числа добавляют букву Q (от английского octal), а в конце шестнадцатеричного числа букву Н (от английского hexadecimal). Например: число  может быть записано 217Q и число
может быть записано 217Q и число  может быть записано 1FC3H.
может быть записано 1FC3H.
1.2. Перевод чисел из одной системы счисления в другую
1.2.1. Перевод чисел из десятичной системы счисления в двоичную
В общем случае перевод целого числа из одной системы счисления в другую выполняется по следующему принципу: для перевода целого числа из Р-системы счисления в К-систему нужно последовательно делить это число и получаемые частные на основание К новой системы, представленное в старой Р-системе, до тех пор, пока частное не станет меньше К. Старшей цифрой в записи числа в К-системе служит последнее частное, а следующие за ней цифры дают остатки, выписываемые в последовательности, обратной их получению. Например, при переводе числа 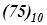 в двоичную систему получим:
в двоичную систему получим:
75½ 2
7437½ 2
1 3618½ 2
1 189 ½ 2
0 84 ½ 2
1 42 ½ 2
0 -2 1 (75)10 = (1001011)2
Для обратного перевода из двоичной, восьмеричной, шестнадцатеричной систем счисления в десятичную можно воспользоваться этим же правилом или представлением числа в виде полинома (1) как это сделано в примерах.
1.2.2. Перевод чисел в двоичной, восьмеричной и шестнадцатеричной системах счисления
Для перевода восьмеричного числа в двоичную систему счисления достаточно заменить каждую цифру восьмеричного числа её представлением в двоичной системе счисления (трехразрядным двоичным числом). Например:

Таким же образом для перехода от шестнадцатеричной системы счисления к двоичной каждая цифра шестнадцатеричного числа заменяется ее представлением в двоичной системе счисления (четырехразрядным двоичным числом), например:

Для перехода от двоичной системы счисления к восьмеричной (или шестнадцатеричной) поступают следующим образом: двигаясь влево, разбивают разряды двоичного числа на группы по три (четыре) разряда. Затем каждую группу из трех (четырех) двоичных разрядов заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой. Например, число 11111110010100011 при переводе в восьмеричную систему счисления будет иметь вид:

Это же число в шестнадцатеричной системе счисления имеет вид:

1.3. Двоичная арифметика
Правила выполнения арифметических действий в двоичной системе счисления определяются таблицами сложения, вычитания и умножения:

Правила арифметики для всех позиционных систем аналогичны, поэтому сложение двух чисел в двоичной системе можно выполнить столбиком, начиная с младшего разряда, подобно тому, как это делается в десятичной системе. В каждом разряде в соответствии с таблицей двоичного сложения производится сложение двух цифр слагаемых или двух этих цифр и 1, если имеется перенос из соседнего младшего разряда. В результате получается цифра соответствующего разряда суммы и, возможно, также единица переноса в старший разряд.
Выполнение операции вычитания в некоторых случаях требует заёма из старших разрядов. При этом необходимо учитывать, что в двоичной системе счисления одна единица старшего разряда равна двум единицам соседнего младшего разряда.
Умножение двоичных многоразрядных чисел производится путем образования частичных произведений и последующего суммирования со сдвигом в соответствии с разрядами множителя. При этом если в разряде множителя 0, то частичное произведение равно нулю, если 1, то - равно множимому. Таким образом, операция умножения многоразрядных двоичных чисел сводится к операциям сдвига и сложения. Примеры выполнения арифметических операций над двоичными числами:
| + (1011011)2 (111000)2 (10010011)2 | -- (11001101)2 (1011110)2 (1101111)2 | * (1011011)2 (101)2 + 1011011 + 0000000 1011011 (111000111)2 |
Благодаря простоте правил двоичного сложения, вычитания и умножения применение в ЭВМ двоичной системы счисления позволяет упростить схемы устройств, выполняющих арифметические операции. При этом обычно аппаратно реализуются простые операции, например сложение и вычитание целых чисел с ограниченным числом разрядов. Для более сложных операций: сложения и вычитания многоразрядных чисел с дробной частью, умножения и деления используются подпрограммы, постоянно находящиеся в вычислительном устройстве.
1.4. Двоично-десятичный код
В случаях, когда цифровое устройство часто обменивается информацией с человеком в привычной для него десятичной системе счисления (например: в калькуляторах, счетчиках, устройствах ввода-вывода, цифровых приборах), используют специальные коды, где десятичные цифры представлены посредством букв двоичного алфавита (0 и 1). Такие коды называют двоично-десятичными или двоично-кодированными десятичными числами.
Способов кодирования существует несколько. Одним из широко применяемых является код 8421, в котором каждая цифра десятичного числа заменяется соответствующим четырехразрядным двоичным числом так же, как и для шестнадцатеричных чисел, но комбинации большие 9 не используются. Например, число (19 205 463)10 в двоично-десятичном коде имеет вид:
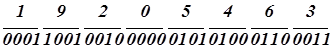 .
.
1.4.1. Арифметические действия над двоично-десятичными кодами
Арифметические действия над двоично-десятичными кодами происходят по более сложным правилам, так как при описании каждого разряда десятичного числа используются не все кодовые комбинации двоичного числа, что затрудняет организацию переноса из разряда в разряд. В устройствах, использующих только двоично-десятичные коды, операция переноса реализуется аппаратно. В ЭВМ, где обрабатываются как двоичные, так и двоично-десятичные числа, используются дополнительные операции.
При выполнении операции сложения одного разряда двух десятичных чисел перенос возникает, если их сумма больше девяти, а в двоичной тетраде (четырех разрядах двоичного числа) перенос будет, если число больше 15. Поэтому если при сложении одного разряда двух двоично-десятичных кодов на двоичном сумматоре сумма получилась больше 9 или есть перенос, то к этому разряду прибавляют ещё число 6 (дополнение до полной кодовой комбинации 15). При этом выполняется перенос в старшую тетраду, а в тетраде складываемого разряда получается число, соответствующее десятичному сложению. И так поступают с каждым разрядом двоично-десятичного кода.
Например, надо сложить два числа (79)10 = (0111 1001) и (38)10 = (0011 1000) в двоично-десятичном коде.
Складываем младший разряд: 1001 + 1000 = 0001 + перенос в следующий десятичный разряд. Проводим десятичную коррекцию (прибавляем число (6) = 0110) и получаем младший разряд суммы 0001 + 0110 = 0111.
Складываем числа следующего десятичного разряда и с учетом переноса получаем: 0111 +0011 + 1(перенос) = 1011. Эта двоичная комбинация соответствует числу, большему 9. Поэтому проводим десятичную коррекцию в этом разряде: 1011 + 0110 = 0001 + (перенос в следующий разряд). В третьем разряде слагаемые имеют цифру 0, с учетом переноса получим двоичный код 0001. Таким образом, двоично-десятичный код суммы имеет вид:

Наличие операций десятичной коррекции увеличивает время вычислений, поэтому в ЭВМ десятичная арифметика используется редко. Чаще вводимые десятичные числа переводятся в двоичную систему счисления и в этой системе обрабатываются. При выводе происходит преобразование результата из двоичной системы в десятичную.
1.5. Вопросы для повторения
1. Что называется системой счисления?
2. Что такое позиционная система счисления?
3. Что такое основание системы счисления?
4. Что такое разряд числа?
5. Какие системы счисления используют в цифровых устройствах?
6. Каковы достоинства двоичной системы счисления?
7. Когда применяется шестнадцатеричная и восьмеричная системы счисления?
8. Когда используется двоично-десятичный код?
2. ДВОИЧНЫЕ КОДЫ ПЕРЕДАЧИ ИНФОРМАЦИИ
И ЗАЩИТА ИХ ОТ ПОМЕХ
2.1. Стандартные коды обмена информацией
Применение алгоритмических языков для записи алгоритмов и автоматизации программирования делает необходимым вводить в цифровые управляющие устройства и ЭВМ не только числовую, но и текстовую (алфавитно-цифровую) информацию, содержащую цифры, буквы, знаки препинания, математические и другие символы. Для передачи информации от одного устройства (например, центральной ЭВМ) к другому (например, системе ЧПУ станка) по каналам связи каждый символ сообщения должен быть представлен последовательностью бит, количество которых определяется принятой системой кодирования. В разное время было разработано несколько кодов, позволяющих передавать алфавитно-цифровую информацию по каналам связи.
Рассмотрим двоичный семиразрядный стандартный код обмена информацией КОИ-7, который приведён в табл. 1. Из семи разрядов старшие три разряда определяются номером столбца, а младшие четыре разряда - номером строки таблицы, на пересечении которых находится кодируемый символ. Сочетаниями букв задаются значения служебных кодовых комбинаций, например: 3В (звонок) - выдача звукового сигнала, ПС (перевод строки) - переход на следующую строку, ВК - возврат курсора или каретки печатающего устройства и т.д.
Таблица 1
     
| |||||||||||||||
| D6 | D5 | D4 | D3 | D2 | D1 | D0 | |||||||||
| A B C D E F | ЗВ ГТ ПС ВК ЛАТ РУС | - ! “ % & , ( ) * + - / | : ; < = > ? | @ A B C D E F G H I J K L M N O | P Q R S T U V W X Y Z [ \ ] ^ | Ю А Б Ц Д Е Ф Г Х И Й К Л М Н О | П Я Р С Т У Ж В Ь М З Ш Э Щ Ч ЗБ |
Рассмотрим, какие коды (в шестнадцатеричной системе) необходимо подать, чтобы на экране дисплея получилось сообщение:
КОД
КОИ-7 .
Для получения такой картины сообщения на экране дисплея необходимо выполнить следующие действия: перейти на новую строку, вывести два пробела, вывести последовательно буквы К, О и Д, перейти на следующую строку, вывести один пробел, вывести последовательно буквы К, О и И, символ -, цифру 7, а затем выдать звуковой сигнал о завершении вывода информации. Этим действиям (см. табл. I) соответствуют коды: 0АН, 20Н, 20Н, 6ВН, 6FH, 64Н, 0AН, 20Н, 6ВН, 6FН, 69Н, 2DН, 37Н, 07Н - всего 14 шестнадцатеричных кодов. Если эти коды последовательно вывести на дисплей, то получим требуемое сообщение.
2.2. Однопеременные коды
Коды, принятые как стандарт для построения каналов связи, относятся к комбинаторным кодам. Комбинаторные коды не обладают арифметическими свойствами, в отличие от арифметических кодов (к которым относятся двоичные числа - их можно складывать, умножать, вычитать), и служат только для кодирования определенной информации.
Одним из важных классов комбинаторных кодов являются однопеременные коды, у которых две смежные кодовые комбинации отличаются только одним изменением в каком-либо разряде (говорят, кодовое расстояние между комбинациями равно 1). Например, два смежных числа (7)10 = (0111)2 и (8)10 = (1000)2 в нормальном двоичном коде отличаются изменениями во всех разрядах, в однопеременных кодах допустимы последовательные комбинации ... 0010, 0011, 0111, 0101 и т.д.
Поясним достоинство однопеременного кода на примере кодового датчика угла поворота. На рис. 1 представлена упрощенная схема датчиков, имеющих кодовую шкалу в простом двоичном коде (рис.1, а) и в однопеременном (рис. 1, б). Элементы, снимающие битовую информацию, изображены кружочками, причем старшие разряды располагаются ближе к центру.

Рис. 1. Схема кодового датчика

Рис. 2. Диаграмма Карнауга
При повороте шкалы с простым двоичным кодом из позиции 3 в позицию 4 и обратно одновременно все три элемента съёма информации располагаются на границе перехода из 0 в 1. Обеспечить одновременное переключение всех трех элементов практически невозможно, а срабатывание какого-либо элемента раньше выдаст ложную информацию, соответствующую другой позиции шкалы, что приведёт к появлению ошибки в работе всей системы управления.
Другая картина наблюдается при повороте шкалы в однопеременном коде, когда переход из одной позиции в другую сопровождается переключением только одного элемента, задержка которого или раннее срабатывание влияет только на точность определения позиции, но ложной информации об угле поворота в этом случае не возникает.
К таким кодам относится код Грея, широко применяемый в системах цифровой автоматики, так как его использование позволяет создавать простые и надежные кодовые датчики. Для построения однопеременных кодов можно использовать диаграмму Карнауга (рис. 2). Диаграмма имеет четыре строки и четыре столбца, их пересечение образует 16 точек, соответствующих кодовым комбинациям. Код в каждой точке получается путем последовательной записи номера строки (два старших двоичных разряда) и номера столбца (два младших двоичных разряда).
Чтобы получить однопеременный код, достаточно наметить определенный путь обхода точек диаграммы и последовательно выписать номера этих точек. Для пути, показанного на рис.2, последовательность кодовых комбинаций имеет вид: 0 - 0000, 1 - 0001, 2 - 0011, 3 - 0010, 4 - 0110, 5 - 0111, 6 - 0101, 7 - 0100, 8 - 1100, 9 - 1101, 10 - 1111, 11 - 1110, 12 - 1010, 13 - 1011, 14 - 1001, 15 - 1000 .
Если однопеременный код отражает количественную информацию, то для того, чтобы ее можно было обрабатывать в вычислительном устройстве (сравнивать, выполнять арифметические действия), она из однопеременного кода переводится в нормальный двоичный код.
2.3. Помехоустойчивое кодирование
В технических устройствах на кодовую комбинацию действуют помехи, от которых комбинация искажается. Помехоустойчивым кодированием называется такое, при котором ошибку можно обнаружить или исправить, или сделать то и другое вместе. Коды, построенные в соответствии с принципами помехоустойчивого кодирования, называются помехоустойчивыми. Наибольшее распространение получили методы информационной избыточности.
Если длина кода n - разрядов, то таким двоичным кодом можно представить максимум 2n различных слов. Если все разряды слова служат для представления информации, то код называется простым (неизбыточным). Например, таким кодом является код КОИ-7. Коды, в которых лишь часть кодовых разрядов используется для представления информации, называются избыточными. Часть слов в избыточных кодах являются запрещёнными, и их появление при передаче информации свидетельствует о наличии ошибки. Принадлежность слова к разрешённым или запрещённым словам определяется правилами кодирования, и для различных кодов эти правила различны.
Способность кода обнаруживать или исправлять ошибки определяется минимальным кодовым расстоянием. Кодовым расстоянием между двумя словами называется число разрядов, в которых слова не совпадают. Минимальным расстоянием данного кода называется минимальное расстояние между двумя любыми словами в этом коде. Если имеется хотя бы одна пара слов, отличающихся друг от друга только в одном разряде, то минимальное расстояние данного кода равно единице.
Простой (неизбыточный) код имеет минимальное расстояние d = 1. Если d >= 2, то любые два слова в данном коде отличаются не менее чем в двух разрядах, следовательно, любая одиночная ошибка приведет к появлению запрещенного слова и может быть обнаружена.
Если d >= 3, то любая одиночная ошибка создает запрещённое слово, отличающееся от правильного в одном разряде, а от любого другого разрешенного слова - в двух разрядах. Заменяя запрещённое слово ближайшим к нему (по кодовому расстоянию) разрешенным словом, можно исправить одиночную ошибку.
Рассмотрим некоторые типичные коды.
2.3.1. Код с проверкой на чётность
Код с проверкой четности образуется добавлением к группе информационных разрядов, представлявших простой (неизбыточный) код, одного избыточного (контрольного) разряда. При формировании кода слова в контрольный разряд записывается 0 или 1 таким образом, чтобы сумма единиц в слове, включая избыточный разряд, была четной в случае контроля на четность (или нечетной в случае контроля на нечетность). Если при передаче информации приемное устройство обнаруживает, что в принятом слове сумма единиц не соответствует четности, то это воспринимается как признак ошибки. Например, при передаче латинской буквы F (см. табл. 1, код 1000110 ) к её двоичному коду будет добавлен контрольный разряд, равный 1, чтобы число всех единиц было четным, и будет передано 11000110, где самый старший, восьмой разряд - контрольный.
Минимальное расстояние кода d = 2, поэтому код с проверкой четности обнаруживает все одиночные ошибки (а также любое нечетное количество ошибок), однако, две ошибки (и любое четное количество ошибок) этот код не обнаруживает.
Код с проверкой четности имеет небольшую избыточность и не требует больших затрат оборудования на реализацию контроля, поэтому широко применяется в вычислительных машинах.
2.3.2. Код Хемминга
Этот код был предложен Р.В. Хеммингом в 1950 году. Он позволяет обнаруживать и исправлять одну ошибку (кодовое расстояние d = 3).
Код Хемминга строится таким образом, что к имеющимся информационным разрядам слова добавляется определенное количество контрольных разрядов, которые формируются перед передачей информации путем подсчета четности суммы единиц для определенных групп информационных разрядов. Контрольная аппаратура на приемном устройстве образует из принятых информационных и контрольных разрядов путем аналогичных подсчетов четности корректирующее число, которое равно нулю при отсутствии ошибки, либо указывает место ошибки, например двоичный порядковый номер ошибочного разряда в слове.
Рассмотрим его более подробно. Допустим, необходимо передать байт информации, т.е. восемь информационных разрядов. Для того чтобы получить число, указывающее на любой разряд этого байта, необходимы четыре двоичных разряда (указание на старший, восьмой разряд в двоичном коде требует четыре разряда 1000). Следовательно, к 8 информационным разрядам необходимо добавить 4 контрольных разряда (избыточные), которые дают корректирующее число. Таким образом, общее число разрядов в передаваемом коде Хемминга в данном случае будет равно 12. Поскольку ошибки могут быть и в контрольных разрядах, то код строится так, чтобы он обнаруживал ошибки в любом разряде; взятых четырех контрольных разрядов для этого достаточно (число 12 в двоичном коде тоже требует 4 двоичных разряда).
Далее полагают, что младший контрольный разряд контролирует четность разрядов, двоичный номер которых имеет единицу в младшем разряде, т.е. 1, 3, 5, 7, 9, 11 разряды (в двоичном коде: 0001, 0011, 0101, 0111, 1001, 1011). Следующий контрольный разряд проверяет разряды, двоичные номера которых имеют единицу во втором разряде, т.е. 2, 3, 6, 7, 10, 11 (в двоичном коде: 0010, 0011, 0110, 0111, 1010, 1011). Третий контрольный разряд контролирует разряды с двоичными номерами, имеющими единицу в третьем разряде, т.е. 4, 5, 6, 7, 12 (двоичные коды: 0100, 0101, 0110, 0111, 1100). Четвертый, старший контрольный разряд контролирует разряды номер 8, 9,10, 11, 12 (в двоичном коде: 1000, 1001, 1010, 1011, 1100).
Для упрощения кодирования в качестве контрольных разрядов берем те, которые встречаются только в одной из перечисленных групп номеров разрядов, т.е. разряды 1, 2, 4, 8. Тогда размещение разрядов в передаваемом коде будет следующим (контрольные разряды подчеркнуты):
D12 D11 D10 D9D8 D7 D6 D5 D4 D3 D2D1.
При этом разряды D12 D11 D10 D9 D7 D6 D5 D3 образуют байт передаваемой информации, а разряды D8 D4 D2 D1 - избыточные, обеспечивают определение и исправление ошибок. Составим таблицу формирования контрольных разрядов (табл. 2).
Таблица 2
| Номер группы | Контрольный разряд | Проверяемые разряды |
| D1 D2 D4 D8 | D1,D3,D5,D7,D9,D11 D2,D3,D6,D7,D10,D11 D4,D5,D6,D7,D12 D8,D9,D10,D11,D12 |
Контрольные разряды формируются следующим образом: им дается значение 0 или 1 так, чтобы сумма проверяемых разрядов согласно табл. 2 была четной.
Например: необходимо передать букву Z. Ее двоичный код имеет вид: 1011010 (см. табл. 1). Передаваемый код Хемминга в информационных разрядах имеет значения: 0101 D8 101 D4 0 D2 D1 и согласно табл. 2 для обеспечения четности суммы проверяемых разрядов контрольные разряды должны иметь значения: D1 = 0, D2 = 0, D4 = 0, D8 = 0. Таким образом, полностью передаваемый код будет иметь вид: 010101010000.
2.3.2.1. Проверка кода Хемминга
После приема передаваемого кода проводится его проверка на наличие ошибки. Для этого определяется корректирующее число путем анализа четности суммы проверяемых разрядов (см. табл. 2). Первая группа дает младший разряд числа, вторая - второй разряд, третья группа - третий, четвертая - старший, четвертый разряд корректирующего числа. Если сумма четная, то соответствующий разряд корректирующего числа равен 0, если нечетная, то разряд равен 1.
Корректирующее число указывает номер разряда, в котором произошел сбой информации, и информацию в этом разряде надо инвертировать. Если корректирующее число равно нулю, то ошибки при передаче не произошло. Предположим, что в рассматриваемом нами коде при приеме возникла ошибка в пятом разряде: 0101010(0)0000.
Для контроля правильности передачи находим корректирующее число, для чего подсчитываем сумму групп проверяемых разрядов согласно табл. 2:
D1+D3+D5+D7+D9+D11 = 0+0+0+1+1+1 = 3,
D2+D3+D6+D7+D10+D11= 0+0+0+1+0+1 = 2,
D4+D5+D6+D7+D12= 0+0+0+1+0 = 1,
D8+D9+D10+D11+D12= 0+1+0+1+0 = 2.
Из анализа четности полученных сумм следует, что корректирующее число имеет значение 0101. Оно указывает (в двоичном коде), что сбой информации произошел в пятом разряде и его необходимо инвертировать. После инверсии пятого разряда получаем верный код: 010101010000 и после того, как уберем контрольные разряды (они подчеркнуты), получим переданную информацию 010 11010.
Допустим, ошибка произошла в 4 разряде 01010101(1)000. В этом случае подсчет сумм по группам проверяемых кодов соответственно дает: 4, 2, 3, 2. Анализ показывает, что только для третьей группы сумма нечетная, значит, корректирующее число имеет вид 0100. Это свидетельствует о сбое в четвертом разряде, но это контрольный разряд, поэтому сразу, не инвертируя, получаем переданную информацию. Возможность исправлять даже только однократные ошибки увеличивает надежность работы цифровых устройств в 200...1000 раз, поэтому подобные коды широко применяются как в каналах связи, так и в запоминающих устройствах.
2.4. Вопросы для повторения
1. Какое максимальное количество команд и символов может быть закодировано семибитным двоичным кодом?
2. Что будет принято по линии связи, если при передаче латинской буквы М будет потеряна единица в третьем разряде (код от помех не защищен)?
3. Какие двоичные коды называются однопеременными?
4. В чем достоинство однопеременных кодов?
5. Какие коды называются помехоустойчивыми?
6. Что такое информационные и контрольные разряды?
7. Что такое кодовое расстояние?
8. Какие возможности имеет код с проверкой четности?
9. Какие возможности имеет код Хемминга?
10. Что такое корректирующее число, и как оно составляется?
3. ИССЛЕДОВАНИЕ ДИСКРЕТНЫХ СХЕМ С ПОМОЩЬЮ АЛГЕБРЫ ЛОГИКИ
3.1. Понятие логической функции и логической переменной
Алгебра логики используется для описания явлений окружающего мира, имеющих два различных уровня и объединенных причинно-следственной связью. К таким явлениям относятся схемы релейной автоматики, электрические цепи которых содержат контактные группы, обмотки реле и сигнальные лампы. Все эти элементы имеют только два состояния: замкнуты - разомкнуты, включены - выключены. В бесконтактной дискретной автоматике и в ЦВМ электрические cигналы имеют два уровня напряжения: нулевой и единичный. В логических доказательствах два значения имеют отдельные высказывания, которые могут быть истинными или ложными, а вся совокупность таких высказываний может подтверждать или отрицать идею, с которой они связаны.
В алгебре логики подобные явления отображаются логическими переменными, которые принимают два значения: 0 или 1. Как и в обычной алгебре, существуют логические функции - логические переменные, зависящие от других переменных, называемых логическими аргументами. На рис. 3 приведен технический пример, в котором лампочка (логическая функция) будет включена (состояние 1) или отключена (состояние 0) в зависимости от состояния ключей Х, Y и Z (логических аргументов), которые могут быть замкнуты (состояние 1) или разомкнуты (состояние 0).

|
Рис. 3. Логическая функция на релейной схеме
Связь логической функции с логическими аргументами может быть описана с помощью таблиц истинности, где в отдельных колонках записываются все возможные состояния аргументов и соответствующие им состояния функции. При этом количество строк будет равно 2n, где n - количество аргументов. Например, для схемы, изображенной на рис. 3, функция будет равна 1, если Z будет равно 1 или X и Y одновременно будут равны 1, и таблица истинности будет иметь вид, представленный в табл. 3.
Таблица 3
| X | Y | Z | F(X,Y,Z) |
Зависимость логической функции от логических аргументов определяется совокупностью логических операций, которые необходимо выполнить над аргументами, чтобы получить функцию.
3.2. Логические операции
3.2.1. Конъюнкция или логическое умножение
Результат этой операции только тогда будет равен 1, когда все переменные, входящие в эту операцию, будут равны 1, иначе результат равен 0. Логическое умножение обозначают знаками "*", если нет арифметических операций, или "&", или "Ù".

Рис. 4. Технические аналоги операции логического умножения
Функция, содержащая только конъюнкцию, аналитически записывается в виде F(X,Y) = X * Y и читается: функция F(X,Y) равна 1, если и Х, и Y равны 1; поэтому логическое умножение называют еще операцией "И". Таблица истинности этой операции представлена в табл.4, а на рис. 4 изображены релейный аналог этой операции (последовательное соединение ключей) и логический элемент бесконтактных схем, выполняющий эту операцию.
Таблица 4
| X | Y | F(X,Y) |
3.2.2. Дизъюнкция или л
Дата добавления: 2022-02-05; просмотров: 325;











