МАТЕРИАЛЫ К ЛАБОРАТОРНОЙ РАБОТЕ

Тема: Алгоритмы разветвляющейся структуры.

Цель: уметь составлять схемы алгоритмов разветвляющейся структуры и программы на языке Turbo-Pascal для решения практических задач.

Студенту следует для трех задач, условия которых приведены ниже, выполнить следующие задания:

· составить схему алгоритма решения задачи;

· записать пояснения к схеме алгоритма;

· составить программу на языке Turbo-Pascal;

· проверить выполнение составленной программы на контрольном примере, приняв упрощенные значения исходных данных по своему усмотрению.

Наиболее наглядным способом составления алгоритма является графический, т. е. изображение алгоритма решения задачи в виде схемы. При составлении алгоритмов разветвляющейся структуры необходимо указать дальнейшее направление вычислительного процесса по одному из нескольких заранее определенных направлений в зависимости от выполнения некоторого логического условия.

При составлении схем алгоритма следует:

· четко определить, что является исходными данными и в каком виде должен получиться результат решения задачи;

· словесно сформулировать действия, которые необходимо выполнить для получения результата решения задачи, затем записать последовательность действий с помощью блоков в виде схемы алгоритма.

ПРИМЕРЫ РАЗНОУРОВНЕВЫХ ЗАДАНИЙ
ДЛЯ КОНТРОЛЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ

ПО МОДУЛЮ

I уровень

Вариант 1

1. Вычислить R при любых заданных значениях xиа:

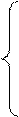
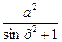, если х < 0;

R=

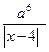, если х ³ 0.

2. Даны три числа a, b, c. Напечатать те из них, которые меньше 15.

3.Взвешивание поросенка показало, что его масса за n дней увеличилась с m1 до m2 кг. Определить, достигнет ли среднесуточный привес поросенка запланированной нормы dкг.

Вариант 2

1. Вычислить Z при любых заданных значениях a, b,t:

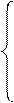
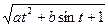, при t < 0,1

Z= at + b , при t = 0,1

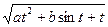, при t > 0,1

2. Даны три числа a, b, c. Напечатать те из них, которые больше 0, но меньше 10.

3. Вывести на экран номера точек с координатами А(x₁, y₁), В(x₂, y₂), С(x₃, y₃), которые лежат на оси ОХ, и определить их количество.

Вариант 3

1. Вычислить S при любых заданных значениях a, b, c, f:

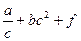, при c < 3;

S= c – cos f , при 3 £ c £ 7;

ac + bc³ , при c > 7.

2. Даны две фигуры: квадрат со стороной a и круг с радиусом r. Определить, какая из фигур имеет бόльшую площадь, и вывести эту площадь на печать.

3. Определить, попадет ли команда “Динамо” в лигу сильнейших (т. е. наберет не менее 20 очков). За выигрыш команда получает 2 очка, за ничью – 1 очко, за проигрыш – 0 очков. Команда m встреч выиграла, k – проиграла, а p завершила вничью.

Вариант 4

1. Вычислить D при любых заданных значениях a, c, x:

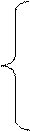
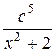, если х < 0;

D =

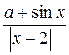, если х ³ 0.

2. Даны три числа a, b, c. Напечатать те из них, которые больше заданной величины z. Если таких чисел нет – вывести сообщение об этом.

3. Определить, можно ли огородить изгородью длиной zдва земельных участка, имеющих форму прямоугольника со сторонами c, d и форму квадрата со стороной a.

Вариант 5

1. Вычислить Z при любых заданных значениях a, b, t:

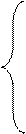
t² + 2a – b, при t < 0,1;

Z= at + b, при t = 0,1;

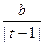, при t > 0,1.

2. Даны три неравных между собой числа a, b, c. Наибольшее из них разделить на сумму двух оставшихся. Вывести на экран полученный результат и наибольшее число.

3. Определить и вывести на экран номера точек с координатами А(x₁, y₁), В(x₂, y₂), С(x₃, y₃), которые лежат на оси ОY.

II уровень

Вариант 6

1. Вычислить C при любых заданных значениях x, a, b:

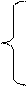а³ – b² +2sinx, если x > а;

C= a² + b² – tgx, если x = а;

а – 2b⁴ + cosx, если x < а.

2. Определить количество неотрицательных чисел среди трех заданных a, b, c . Если таких чисел нет – вывести об этом сообщение.

3. Деревня А находится на расстоянии c км от железнодорожной станции и на расстоянии r км от другой деревни В (рисунок 8).

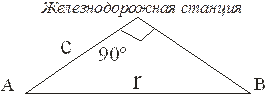
Рисунок 8

Определить, какая из деревень находится ближе к станции, напечатать сообщение об этом.

Вариант 7

1. Вычислить D при любых заданных значениях x, a:

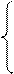(x – a)², если х > 0;

D= 2x + a, если х = 0;

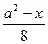, если х < 0.

2. Определить, является ли число b наименьшим из четырех, не равных между собой a, b, c, d.

3. Даны две фигуры: квадрат со стороной a и прямоугольник со сторонами c, d. Определить, какая из фигур имеет больший периметр, и вывести сообщение об этом на печать.

Вариант 8

1. Вычислить C при любых заданных значениях x, a:

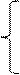ах² – 4, если x< –2;

x⁴ – 1, если –2 £ x < 0;

C= х³ + 8х, если 0 £ x < 2;

4sinx, если x ≥ 2.

2. Определить, могут ли произвольные числа a, b, c служить длинами сторон треугольника.

3. Имеются 3 клубня шарообразной формы радиусами r1, r2, r3. Определить, сколько из них пройдет через круглое отверстие сепарирующего решета площадью s.

Вариант 9

1. Вычислить D для любых произвольных значений x, c:

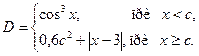
2. Составить алгоритм вычисления действительных корней квадратного уравнения ax²+ bx + c= 0 по формулам:
x_1,2 = 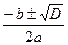, где D = b² –4ac.

3. Даны три действительных числа a, b, c.Вывести на печать те из них, которые принадлежать отрезку 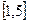,если таких чисел нет, то вывести на печать сообщение об этом.

Вариант 10

1. Вычислить C при любых заданных значениях x, a, b:

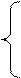а² – b² +2sinx², если x > а;

C= a² +b – tgx, если x = а;

а – 2b⁴ + cosx, если x < а.

2. Даны три числа a, b, c. Определить, есть ли среди них отрицательные, вывести соответствующее сообщение на экран.

3. При осмотре леса лесник определил численность деревьев на контрольном участке: сосен – N1, елей – N2, берез – N3. Из них здоровыми являются соответственно M1, M2, M3, остальные повреждены. Определить, какого вида деревьев больше всего повреждено и вывести сообщение на печать.

Вариант 11

1. Вычислить F при любых заданных значениях x, c:

D=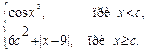

2. Вычислить Q = max (x, y, z) + x³. Значение x, y, z заданы.

3. Суточная норма кормления одной коровы составляет a кг сена, одной лошади – b кг сена. Определить, можно ли прокормить k коров и m лошадей в течение n дней, располагая массой pкг сена, если нет, то определить, сколько кг сена не хватает.

Вариант 12

1. Вычислить S при любых заданных значениях x, c:

S=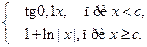

2. Среди 3-х точек с координатами (x₁,y₁), (x₂,y₂),(x₃,y₃) определить количество точек, лежащих в 3-ей четверти.

3. В колхозе имеется 3 комбайна ККУ-2А со средней производительностью sга в день и 5 комбайнов КПК-3 со средней производительностью p га в день. Будет ли выполнена колхозом уборка поля площадью s га в запланированный срок, составляющий 10 дней?

Вариант 13

1. Вычислить D при любых заданных значениях a, x:

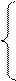|x| + a – 4, если а > 2;

D= 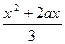, если а = 2;

4х + a, если а < 2.

2. Даны две фигуры: квадрат со стороной a и круг с длиной окружности L. Определить, какая из фигур имеет большую площадь, и вывести эту площадь на печать.

3. Имеется 10 круглых луковиц диаметром d1, 6 луковиц диаметром d2 и 15 луковиц диаметром d3. Радиус отверстия в сепарирующем решете p. Определить, сколько луковиц пройдет сквозь отверстие решета.

Вариант 14

1. Вычислить C при любых заданных значениях d, x:

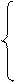сosx² + d + 1, если d > 1;

C= 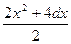, если d = 1;

8х – d , если d < 1.

2. Заданы 4 неравных между собой числа a, b, c, d. Определить наибольшее из них и вывести на печать.

3. В квадрат со стороной x вписан круг. Определить, площадь какой фигуры больше: квадрата или круга и вывести сообщение на печать.

Вариант 15

1. Вычислить F при любых заданных значениях x, c:

|x| + x – 4, если x > 0.2

F= 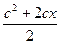, если x = 0.2

cos²x – 1, если x < 0.2

2. Среди 3-х точек с координатами (x₁,y₁), (x₂,y₂),(x₃,y₃) определить количество точек, лежащих в 4-ой четверти.

3. Каждая из трех доярок надоила за месяц (30 дней) соответственно Р1, Р2, Р3 литров молока. Определить, у какой доярки наибольший среднесуточный надой молока и вывести на экран ее номер.

Вариант 16

1. Вычислить T при любых заданных значениях a, d, b, c:

5, если d < a;

T= 4, если а ≤ d ≤ b;

3, если b < d < c;

2, если d ≥ c.

2. Определить количество положительных чисел среди четырех a, b, c, d .

3. Определить, можно ли огородить изгородью длиной r земельный участок, имеющий форму равнобедренной трапеции с основаниями c, d и высотой h.

Вариант 17

1. Вычислить D при любых заданных значениях x, a, z:

|ax – 3|, если х < 2;

D =8x – 1, если 2 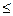х < 3;

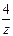+ a³, если x 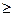3.

2. Определить, какая из сторон k, l, m прямоугольного треугольника является его гипотенузой, и вывести ее значение на печать.

3. Определить, какая из трех точек с координатами А(x₁, y₁), В(x₂, y₂), С(x₃, y₃) наиболее удалена от начала координат и вывести на печать ее номер.

Вариант 18

1. Вычислить Z при любых заданных значениях a, b, x, c:

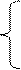ax²/2 + bx – c, если x 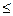1;

Z= x + 1,5, если 1 < х < 2;

2x² – b, если x ³ 2.

2. Проверить, является ли треугольник со сторонами a, b, c равнобедренным и вывести на экран соответствующее сообщение.

3. Даны две фигуры: квадрат с диагональю d ипрямоугольная трапеция со сторонами x, y, z(рисунок 9). Определить, какая из фигур имеет больший периметр, сообщение вывести на печать.

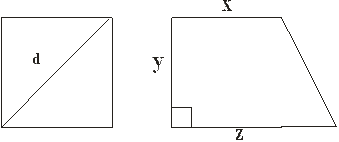
Рисунок 9 – Квадрат с диагональю d ипрямоугольная трапеция со сторонами x, y, z

Вариант 19

1. Вычислить Tдля любых произвольных значений х и с:

T =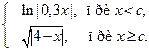

2. В прямоугольном треугольнике заданы три стороны k, l, m.Вывести на печать значение гипотенузы и найти площадь треугольника.

3. Заданы четыре переменные x, y , z , d. Найти и вывести на печать количество переменных, попавших в интервал от –5 до 5, если таких нет – дать сообщение.

Вариант 20

1. Вычислить Dпри любых заданных значениях x, a, b:

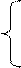ax + b, при х £ 0;

D= |b| – 2, при 0 < x £ 1;

|а| – х², при х >1.

2. Вычислить Q = min (a, b, c) + z. Значения a, b, c, z заданы.

3. Даны две фигуры: квадрат с диагональю d ипрямоугольная трапеция со сторонами x, y, z. Определить, какая фигура имеет большую площадь, сообщение вывести на печать (см. рисунок 9).

Вариант 21

1. Вычислить Y при любых заданных значениях a, x, b:

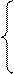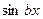, при x < a;

Y= сosax, при а £ x £ b;

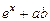, при x > b.

2. Среди 3-х точек с координатами (x₁,y₁), (x₂,y₂),(x₃,y₃) определить количество точек, лежащих в 1-ой четверти.

3. Имеются четыре результата t1, t2, t3, t4 (сек.) в беге на 100 метров. Вывести на печать результат и номер победителя.

Вариант 22

1. Вычислить Z при любых заданных значениях a:

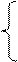asinx², если a ≤ –3;

Z= 1, если –3 < a < 4;

сos(a + 1) , если a ≥ 4.

2. Среди 3-х точек с координатами (x₁,y₁), (x₂,y₂),(x₃.y₃) определить количество точек, лежащих в 2-ой четверти и вывести на экран их координаты.

3. Четыре студента сдали экзамен по физике и получили соответственно оценки x, y, z, d.Определить и вывести на печать номера студентов, оценка которых превышает средний балл по предмету.

Вариант 23

1. Вычислить S при любых заданных значениях a, b, c:

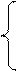
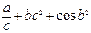, при c < 3;

S= cos³a – c, при 3 £ c £ 7;

ac + bc³ + 2, при c > 7.

2. Даны две фигуры: квадрат с периметром z и круг с длиной окружности c. Определить, какая из фигур имеет большую площадь, и вывести эту площадь на печать.

3. Четыре студента сдали экзамен по физике и получили соответственно оценки a, b, c, d.Определить и вывести на печать количество и номера студентов, которые получили по экзамену оценку 9.

Вариант 24

1. Вычислить Zпри любых заданных значениях x:

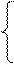x³ – 3x + 8, при х £ 0;

Z= 4, при 0 < x £ 1;

1 / (x³ – 3x + 8), при х >1.

2. Среди трех чисел a, b, c есть пара равных. Заменить их нулями и все числа вывести на печать.

3. Имеются четыре результата z1, z2, z3, z4 (м) по прыжкам в высоту. Вывести на печать количество и номера спортсменом, которые прыгнули выше заданного норматива L(м).

III уровень

Вариант 25

1. Вычислить U при любых заданных значениях x, a, b:

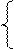x² – 3a + cos²x, при х £ 3;

U = |b – a|, при 3 < x £ 5;

(x³ – 4), при x >5.

2. Определить, является ли треугольник со сторонами a, b, c прямоугольным (для определения использовать теорему Пифагора).

3. Определить, какая из трех точек с координатами А(x₁, y₁), В(x₂, y₂), С(x₃, y₃) лежит ближе к началу координат и вывести на печать ее номер.

Вариант 26

1. Вычислить Fдля любых произвольных значений х и с:

F =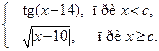

2. Задана окружность с центром в начале координат и точка Ас координатами (x, y), лежащая на окружности. Определить, можно ли в этот круг вписать квадрат со стороной d.

3. Надои молока, полученные каждой из трех доярок Петровой, Ивановой, Сидоровой за 30 дней, составляют соответственно Р1, Р2, Р3 литров. Вывести на печать фамилии и надои тех доярок, среднесуточные надои которых достигают планового показателя, равного R литров.

Вариант 27

1. Вычислить R при любых заданных значениях x, a, b:

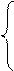
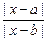, если x < a;

R= x – a + b, если x = а;

ba – cos² x, если x > a.

2. Бригада из четырех рабочих собирала картофель, каждый собрал соответственно a, b, c, d (кг). Определить, превышает ли средняя выработка в бригаде заданную величину S (кг) и вывести на печать номера рабочих, которые не достигли средней выработки по бригаде.

3. Даны три неравных между собой числа x, y, z. Наибольшее из них разделить на сумму двух других.

Вариант 28

1. Вычислить Dдля любых произвольных значений х и с:

D =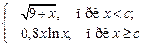

2. Определить, поместится ли круг с радиусом rвквадрат со стороной a.

3. Три студента сдали три экзамена и получили соответственно оценки: I студент – x1, x2, x3;II студент –y1, y2, y3;III студент– z1, z2, z3.Вывести на печать номера тех студентов, которые будут получать стипендию, если для этого необходимо иметь средний балл, равный 7,5.

Вариант 29

1. Вычислить G для любых произвольных значений х и с:

G =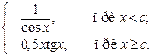

2. Вычислить Q = max (x, y, z) + 4. Значение x, y, z заданы.

3. Заданы три точки с координатами А(x₁, y₁), В(x₂, y₂), С(x₃, y₃) и круг c центром в начале координат и радиусом R. Определить, сколько точек принадлежит кругу.

Вариант 30

1. Вычислить Bдля любых произвольных значений х и с:

B =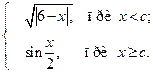

2. Вычислить Q = min (x, y, z) + d. Значение x, y, z, dзаданы.

3. Цех по переработке молочной продукции за одну смену выпускает пастеризованного молока a кг, кефира – b кг. Определить, выполнит ли цех плановые показатели за месяц (30 дней) по каждому из видов продукции, составляющих соответственно s кг и p кг, если в первую декаду он работал в одну смену, во вторую – в полторы, в третью – в две смены.