Теплоотдача при ламинарном пограничном слое

Для расчета теплоотдачи при ламинарном пограничном слое используем уравнение (6.3). Чтобы рассчитать теплоотдачу, необходимо знать распределение скорости в слое.

Аппроксимация профиля скорости.Распределение скорости в ламинарном пограничном слое по форме близко к параболе. Кривую распределения скорости удобно описать уравнением кубической параболы

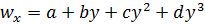. (а)

Уравнение распределения скорости должно удовлетворять граничным условиям. При 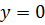выполняется 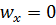(условие «прилипания»); полагаем также, что 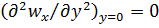. Кроме того, на внешней границе пограничного слоя 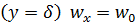и .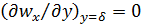

Условие 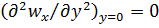следует из дифференциального уравнения движения (5.28), если полагать, что непосредственно у стенки в жидкости актуальны только силы вязкости (т.е. силами инерции можно пренебречь).

Уравнение (а) будет удовлетворять перечисленным граничным условиям, если

.

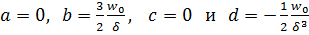Распределение скорости при этом примет вид:

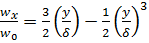. (б)

При распределении скорости согласно (б) из интегрального уравнения импульсов (6.5) можно получить, что толщина гидродинамического пограничного слоя определяется выражением

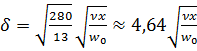. (6.6)

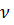- кинематическая вязкость.

Формула (6.6) показывает, что 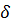меняется пропорционально корню квадратному из расстояния от переднего края пластины до данной точки. Этой формуле можно придать безразмерный вид:

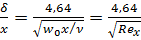. (6.7)

Аппроксимация профиля температуры. Примем, что температура поверхности тела 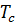не зависит от 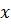, т.е. 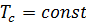. Для удобства температуру жидкости будем отсчитывать от 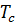. Обозначим:

; ,

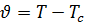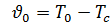где 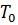– температура жидкости за пределами теплового пограничного слоя. При этом граничные условия оказываются аналогичными ранее принятым условиям для гидродинамического пограничного слоя.

Действительно, при 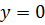имеем 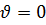. Кроме того, 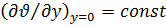и 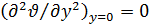, если учесть, что в жидкости, непосредственно прилегающей к плоской стенке, теплота переносится по 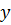только теплопроводностью. На внешней границе теплового слоя 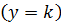справедливы условия

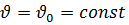и .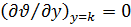

В результате получаем, что распределение температуры описывается уравнением, аналогичным по форме записи уравнению распределения скорости

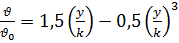. (в)

Из (в) следует, что

;

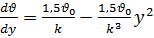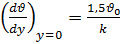. (г)

Толщина теплового пограничного слоя.Вычислим интеграл уравнения теплового потока (6.3), интегрируя в пределах теплового пограничного слоя от 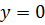до 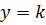. Предварительно примем, что 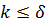. В этом случае интегрирование в пределах от 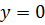до 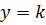является интегрированием в пределах и теплового, и гидродинамического слоев.

Если распространить интегрирование на случай 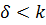, то это означало бы, что в пределах теплового пограничного слоя имеют место два закона распределения скоростей; при 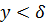– согласно уравнению (б) и при 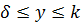– согласно условию .

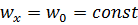Интегрирование дает:

.

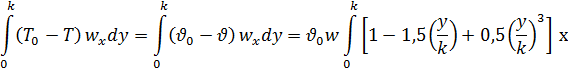
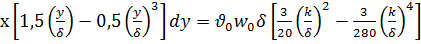Так как 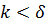, то 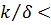1, а поэтому второй член в скобках в правой части равенства мал по сравнению с первым и им можно пренебречь. Подставив значение интеграла и значение 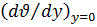согласно (г) в (6.3), получим

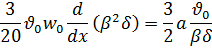
или

,

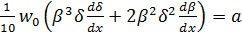где .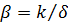

Исходя из аналогии уравнений теплового и динамического пограничных слоев при аналогичности принятых нами распределений скорости и температуры (б) и (в), можно полагать, что толщины теплового и динамического слоев 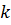и 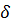зависят от 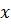одинаково и их отношение равно постоянной величине[1], не являющейся функцией 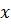. Тогда 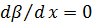и вместо предыдущего уравнения получаем:

.

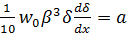Из уравнения (6.6) следует, что

.

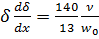Подставляя это значение в предыдущее уравнение и полагая, что

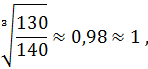
получаем:

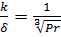. (6.8)

Такой же результат дают и более точные решения.

Подставляя значение 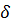согласно (6.7) в уравнение (6.8), получаем:

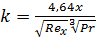, (6.9)

где .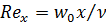

Для капельных жидкостей, как правило, 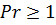и, следовательно, 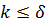, т.е. выполняется условие, принятое при интегрировании уравнения теплового потока. Число Прандтля газов изменяется в пределах примерно от 0,6 до 1; в частности, для воздуха 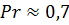в большом интервале температур. При этом 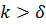, однако разница в толщинах теплового и гидродинамического слоев невелика. Например, при 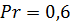имеем 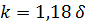. Опыт показывает, что указанным различием и практически можно пренебречь.

Для жидких металлов 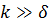, для них полученные результаты непригодны.

Коэффициент теплоотдачи. Опуская знак минус, из уравнений (5.22) и (г) получаем:

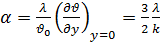. (6.10)

Следовательно, коэффициент теплоотдачи обратно пропорционален толщине пограничного слоя.

Уравнение (6.10) можно привести к безразмерному виду. Для этого умножим левую и правую части на 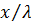и подставим значение 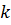согласно (6.9), получим:

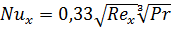, (6.11)

где

;

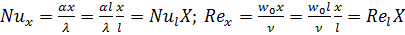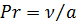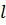; - длина пластины вдоль потока.

Уравнение (6.11) можно записать следующим образом:

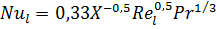. (6.12)

Отсюда следует, что

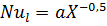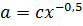или . (д)

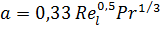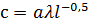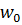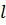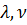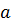Величины и , содержащие коэффициент пропорциональности 0,33, скорость , длину пластины и физические параметры и , от 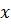не зависят.

Согласно (д) при 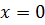значение коэффициента теплоотдачи бесконечно велико, при увеличении 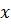он принимает конечные и постоянно уменьшающиеся значения (рис.6.2). Такой характер изменения 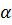объясняется тем, что температурный напор 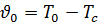не изменяется вдоль пластины, в то время как температурный градиент на стенке непрерывно уменьшается с ростом 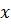– см. уравнения (г) и (6.9).

Рисунок 6.2. Изменение коэффициента теплоотдачи вдоль

пластины при ламинарном пограничном слое

Формула (6.11) получена при условии, что температура поверхности пластины постоянна, физические параметры жидкости не зависят от температуры и в начале пластины нет необогреваемого участка. Как показывают опыт и теория, неучет этих факторов может привести к значительным ошибкам.

[1] Это утверждение справедливо, если не только гидродинамический, но и тепловой слой развиваются с самого начала пластины 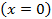, т.е. в начальной части пластины нет необогреваемого участка.