Интегральные уравнения пограничного слоя

ТЕПЛООТДАЧА ПРИ ВЫНУЖДЕННОМ ПРОДОЛЬНОМ ОМЫВАНИИ ПЛОСКОЙ ПОВЕРХНОСТИ

Для простоты будем полагать, что плоская поверхность омывается потоком несжимаемой жидкости, скорость и температура которой за пределами гидродинамического и теплового пограничных слоев постоянны и равны соответственно 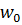и .

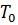Поток направлен вдоль пластины, температура поверхности тела во времени не изменяется. Внутренние источники теплоты в жидкости отсутствуют, теплота трения пренебрежимо мала.

Интегральные уравнения пограничного слоя

Уравнение теплового потока. В гл. 5 была предложена упрощенная запись дифференциального уравнения энергии для теплового пограничного слоя (5.30). Учитывая, что 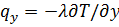и, следовательно, 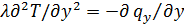, уравнение (5.30) представим в виде

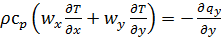. (6.1)

Проинтегрируем это уравнение в пределах от 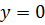до 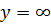. Напомним, что за пределами пограничного слоя производные, входящие в уравнение (6.1), равны нулю по определению (см. §5.3). Поэтому увеличение верхнего предела от 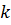до 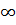не дает изменения интеграла. Интегрирование правой части уравнения дает:

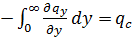; (а)

здесь учтено, что 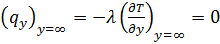(см. §5.3).

Прежде чем взять интеграл от левой части уравнения (6.1), из уравнения сплошности (5.29) ( 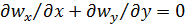) выразим 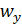. Из (5.29) имеем:

;

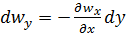учитывая, что при 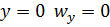в силу непроницаемости стенки, получаем:

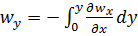. (6.2)

Подставляя значение 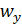в (6.1) и интегрируя левую часть, получаем:

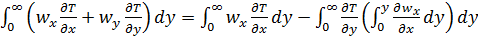. (б)

Второй интеграл правой части последнего уравнения можно брать по частям. Формула интегрирования по частям следующая:

,

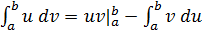тогда

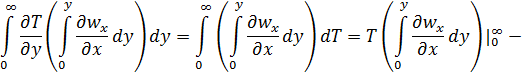
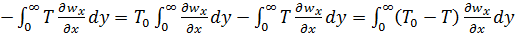. (в)

Подставим выражение (в) в уравнение (б). Поскольку пределы интегрирования не зависят от 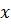, последовательность операций дифференцирования по 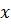и интегрирования по 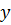может быть изменена. Учитывая последнее, получаем:

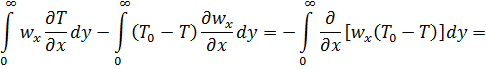
. (г)

Приравнивая уравнения (а) и (г) и переходя от предела интегрирования 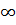к пределу 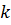, получаем следующее интегродифференциальное уравнение:

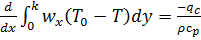. (6.3)

Это уравнение называют интегральным уравнением теплового потока для теплового пограничного слоя. Здесь интеграл левой части и 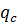являются функциями только 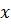. При приближенных расчетах функциям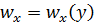и и 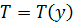часто задаются, исходя из накопленного опыта. Следует отметить, что левая часть уравнения (6.3) достаточно нечувствительна (устойчива) к некоторым неточностям выбора распределени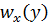й и 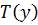. Если известны распределения скорости и температуры, то с помощью уравнения (6.3) можно определить 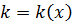. Пример такого решения будет показан в следующем параграфе.

Уравнение импульсов. Уравнение движения в проекциях на ось 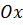для рассматриваемого здесь течения было записано в приближении пограничного слоя в гл. 5 – см. уравнение (5.28). Учитывая, что 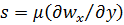, представим уравнение (5.28) в следующей записи:

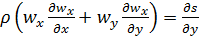. (6.4)

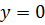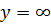Из сравнения уравнения (6.1) и (6.4) следует их полная аналогия. Отсюда при интегрировании (6.4) в пределах от до (или 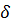), выполняя аналогичные преобразования, получаем интегральное уравнение импульсов для гидродинамического слоя в следующем виде:

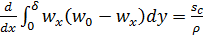, (6.5)

где 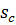– касательное напряжение трения при 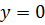, т.е. на поверхности стенки.

Интегральные уравнения теплового и гидродинамического пограничного слоя (6.3) и (6.5) справедливы при выполнении раннее принятых условий. В более общем случае усложняются и соответствующие ему интегральные уравнения.

Физический смысл интегралов, стоящих в левых частях уравнений (6.3) и (6.5). С помощью двух сечений, отстоящих друг от друга на расстоянии 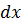, выделим в тепловом пограничном слое бесконечно малый объем (рис.6.1). Плоскости, ограничивающие выделенный объем параллельно плоскости чертежа, находятся друг от друга на расстоянии, условно принимаемом за единицу. Аналогичное выделение контрольного объема предполагается и для гидродинамического пограничного слоя.

Рисунок 6.1. К получению интегрального уравнения теплового потока

Массовый расход жидкости в определенном сечении пограничного слоя и изменение этого расхода на единице длины будут соответственно равны:

.

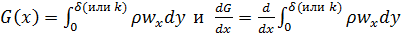Вместе с массой переносятся количество движения 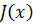и энтальпия 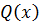. Изменения 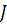и 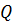на единице длины определяются соответственно уравнениями

.

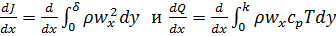Эти изменения связаны с приходом количества движения 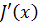и энтальпии 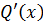через внешнюю границу пограничных слоев 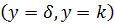вместе с массой жидкости, вовлекаемой в течение в пограничном слое (рис.6.1):

.

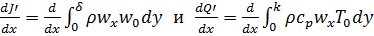Кроме того, изменения 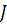и 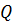обусловлены вязким сопротивлением трения и тепловым потоком на поверхности стенк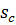и и .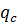

Тогда уравнения (6.3) и (6.5) могут быть записаны соответственно в следующем виде:

.

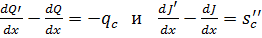Интегральное уравнение теплового потока (6.3) впервые получено Г.Н.Кружилиным, а уравнение импульсов (6.5) – Т.Карманом. Эти уравнения пригодны и для турбулентного пограничного слоя, если под 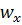и 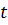подразумевать осредненные во времени значения скорости и температуры. Напомним, что на твердой непроницаемой стенке 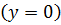должны выполняться равенства 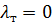и 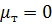, что и учтено при получении уравнений (6.3) и (6.5).