Классификация математических моделей

Математическая модель или оператор системы (системный оператор) – это формальное (количественное) описание системы с помощью математических средств: дифференциальных, интегральных, разностных, алгебраических уравнений, - а также неравенств, множеств и т.д.

Пользуясь понятием системного оператора, можно на единой основе рассмотреть понятие математической модели.

Пусть Uи X–множество входных и выходных сигналов системы. Если каждому элементу u Î Uставится в соответствие определенный элемент x Î X,то говорят, что задан системный оператор.

Связь между входом и выходом задается посредством системного оператора. A:

A x = u и x= A^-1 u(*)

Уравнение (*) с оператором A следует считать математической моделью, поскольку оно устанавливает количественную связь между входом u(t) и выходом x(t) системы.

В зависимости от того, какими классами дифференциальных уравнений описываются системы, их можно классифицировать так, как показано на рисунке 3.5.

Детерминированными называются модели, в которых все параметры являются детерминированными (неслучайными).

Вероятностными считаются модели, в которых все или часть параметров носит случайный характер.

Модели относятся к моделям с сосредоточенными параметрами, если поведение систем описывается обыкновенными дифференциальными уравнениями.

Модели относятся к моделям с распределенными параметрами, если поведение систем описывается дифференциальными уравнениями в частных производных.

Линейными называются математические модели, которые описывают поведение системы линейными операторными уравнениями, в противном случае модели – нелинейные.

Модель одномерна, если векторы входа и выхода одномерные, иначе – многомерна.

Односвязные модели содержат один операторA (в моделях по входу-выходу) либо пару операторов F и G (в моделях в пространстве состояний).

Соответственно многосвязные модели содержат несколько операторов A и несколько пар операторов F и G.

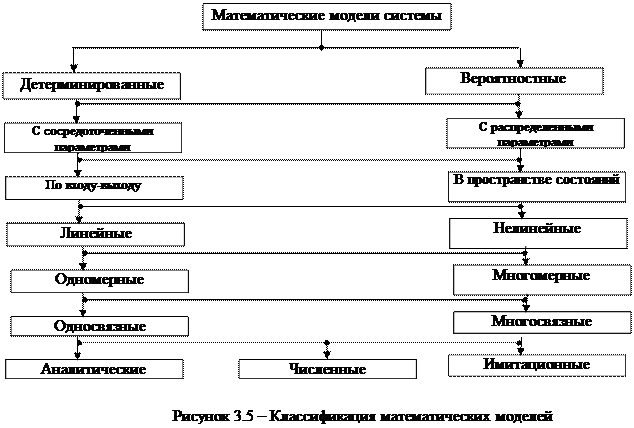
Аналитические модели дают описание процессов, происходящих в системе в виде некоторых функциональных соотношений.

Численные модели дают результаты в виде частных численных решений характеристик системы.

Имитационные модели служат для воспроизведения процесса функционирования сложных систем. Основное преимущество имитационных моделей - это решение задач исключительной сложности. Имитационные модели дают решения частного характера, отвечающие фиксированным значениям параметров системы, входной информации и начальным условиям.