Правильные многоугольники

Многоугольник называется правильным, если он имеет равные стороны и равные углы.

Теорема. Если разделить окружность на n равных частей, то:

1. Точки деления служат вершинами правильного многоугольника (при этом получаем вписанный многоугольник)

2. Касательные к окружности в этих точках служат сторонами второго правильного многоугольника (при этом получаем описанный многоугольник)

Доказательство:

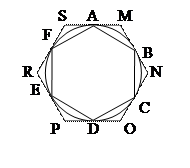Пусть окружность разделена на несколько равных частей в точках А,В,…F и через эти точки проведены хорды АВ, ВС, …FA и касательные MBN, NCO,… SAM.

Тогда:

1. Вписанный многоугольник правильный, т.к. все его стороны равны как хорды, стягивающие равные дуги, и все углы равны, как вписанные, опирающиеся на равные дуги.

2. Описанный многоугольник MNOP…S – правильный. Для доказательства рассмотрим треугольники DАМВ, D NBC… В них АВ=ВС=… (как хорды, стягивающие равные дуги), ÐMAB=ÐMBA=ÐNBC=…(почему?

)

Значит, эти треугольники равнобедренные и равные. Тогда MN=MB+BN, причем MB=BN=…, следовательно, стороны многоугольника равные: MN=NO=OP=… и углы ÐM=ÐN=ÐO=…(почему?

)

Значит, многоугольник правильный.

Общий центр окружностей описанной около правильного многоугольника и вписанной в него называется центром многоугольника. Радиус вписанной окружности называется апофемой.

Замечание: Если в окружность можно вписать правильный n-угольник, то можно вписать и правильный 2n-угольник. Для этого достаточно разделить на две части дугу, стягиваемую стороной n-угольника.

Теорема: Пусть P – периметр правильного описанного около окружности многоугольника, р- периметр вписанного многоугольника с тем же числом сторон. Если безгранично удваивать число сторон, то величины Р и р стремятся к одному и тому же пределу L.

Доказательство:

Докажем эту теорему, основываясь на следующих соображениях:

1. Периметры р (периметры вписанных многоугольников, стороны которых удваиваются) возрастают, т.к. предыдущий многоугольник лежит внутри следующего, но остаются все время меньше некоторого постоянного значения. Следовательно, последовательность периметров р имеет предел

2. Периметры Р (периметры описанных многоугольников, стороны которых удваиваются) убывают, т.к. следующий многоугольник лежит внутри предыдущего, но остаются все время больше некоторого постоянного значения. Следовательно, последовательность периметров Р имеет предел

3. Докажем, что эти пределы равны. Два правильных многоугольника, описанный и вписанный, с одинаковым числом сторон, подобны, и их периметры относятся как их апофемы: 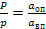, (почему?

)

где 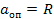, 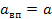. Но при неограниченном удвоении сторон 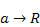, т.е. 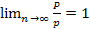, откуда получаем, что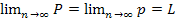

Длина L, общий предел периметров вписанного и описанного n-угольников, количество сторон которых неограниченно возрастает, называется длинной окружности.

Теорема: Длины двух любых окружностей относятся как их радиусы.

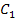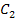Доказательство:Пусть и - длины окружностей радиусов 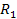и 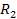. Впишем в эти окружности два правильных многоугольника с одинаковым числом сторон. Они будут подобны, тогда их периметры относятся как 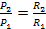. Поскольку отношение периметров в пределе даст отношение длин окружностей, то .

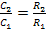Замечание: Из этой теоремы легко видеть, что отношение длины окружности к ее радиусу есть величина постоянная, которую обозначают .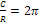

p - некоторая константа, следовательно, ее значение можно вычислить. Впервые обозначением этого числа греческой буквой p воспользовался британский математик Джонс (1706), а общепринятым оно стало после работ Эйлера. Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр. Для вычисления этого значения существует множество способов. В настоящее время значение для числа p вычислено с точностью до ста миллиардов знаков после запятой. p» 3,141 592 653 589 793 238 462… Существует праздник, посвященный этому числу. День числа p отмечается 14 марта и совпадает с днем рождения одного из наиболее выдающихся физиков современности - Альберта Эйнштейна.