Программа решения системы линейных алгебраических уравнений
Эффективность использования ЭВМ проявляется только при реализации алгоритмов, которые основаны на многократном повторении одних и тех же операций на большом количестве однотипных информационных объектов.
Повторение однотипных действий описывается на языке программирования операторами цикла. Перебор множества однотипных объектов легко осуществим, если эти объекты наделены общим именем и строго упорядочены, т.е. прономерованы.
Опр. Упорядоченная совокупность однотипных объектов различимых одним индексом { 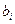 } , i=1,2,…n образуют математический объект – вектор
} , i=1,2,…n образуют математический объект – вектор 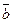 и его аналог в программировании – одномерный массив:
и его аналог в программировании – одномерный массив:
Var b: array [1…N] of real;
где отдельный 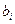 -ый элемент совокупности именуется b[i].
-ый элемент совокупности именуется b[i].
Опр. Упорядоченная совокупность однотипных объектов, различимых по двум индексам { aij }, i=1,2…k, j=1,2,…m, образует математический объект – матрицу, а в программировании – двумерный массив
Var a: array [1..k, 1..m] of real;
а отдельный aij-элемент именуется а[i, j].
Примечание: Упорядоченность информационных объектов по k-индексам формализуем k-мерным массивом.
Для освоения техники использования индексированных переменных напишем программу решения системы линейных алгебраических уравнений: найти числа {xi}, i=1,2,…n, удовлетворяющие уравнениям:
i j = 1 2 3 … . . j . . . . . n

 1 a11x1+a12x2+a13x3+...+a1jxj ...+a1nxn =b1
1 a11x1+a12x2+a13x3+...+a1jxj ...+a1nxn =b1
2 a21x1+a22x2+a23x3+...+a2jxj...+a2nxn =b2 (1)
3 a31x1+a32x2+a33x3+...+a3jxn...+a3nxn =b3
. . . . . . . . .
n an1x1+an2x2+an3x3+...+anjnj...+annxn =bn
Матричная формула записи задачи (1): А  =
= 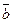 (2)
(2)
где А = {aij}  = {xi}
= {xi} 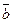 = {bi} i=1,2…n, j=1,2,…n
= {bi} i=1,2…n, j=1,2,…n
Запись системы (1) посредством символа суммирования:
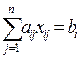 , для i=1, 2…n (3)
, для i=1, 2…n (3)
Систему уравнений (1) решаем методом последовательного исключения Гаусса.
Целью первого этапа этого метода является преобразование матрицы к треугольному виду, т.е. обнуление всех коэффициентов матрицы, расположенных ниже главной диагонали, что формализуется записью:
aij=0 для всех i > j (4)
Алгоритм первого этапа:
1) Полагая 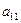 ≠ 0, делим первое уравнение системы (1) на
≠ 0, делим первое уравнение системы (1) на 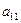 , т.е. приводим его к виду
, т.е. приводим его к виду
1∙ 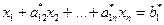 (5)
(5)
где 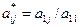 j = 1,2,3….n (6)
j = 1,2,3….n (6)
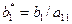 (7)
(7)
Эти действия на языке Pascal описываются операторами:
R:=A[1,1]; {сохранили значение коэффициента 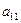
в рабочей переменной с именем R}
for j:=1 to N do a[1, j]:=a[1, j]/R; {вычислили значение 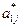 и разместили их в
и разместили их в
тех же местах памяти, где ранее были значения 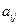 }
}
b[1]:=b[1]/R;
Вопрос для самопроверки: почему нельзя описывать вычисления 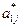 операторами:
операторами:
for j: =1 to N do a [1,j] : = a [1,j]/a [1,1]; b [1] : = b [1]/a[1,1];
2) С помощью преобразованного первого уравнения (5) легко исключить (обнулить) первые слагаемые из всех остальных уравнений системы, т.е. обнулить все 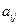 для i=2,3,…n, т.е. обнулить первый столбец матрицы. Для этого необходимо из каждого i-го уравнения (i=2,3,…n) вычесть первое уравнение, т.е. (5) предварительно умножив его на
для i=2,3,…n, т.е. обнулить первый столбец матрицы. Для этого необходимо из каждого i-го уравнения (i=2,3,…n) вычесть первое уравнение, т.е. (5) предварительно умножив его на 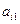 .
.
Математически это записывается так: для всех i=2,3,…n и j=1, 2, ...n вычислить новые (пересчитать) коэффициенты
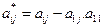 и
и 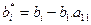 (8)
(8)
На языке Pascal, эти инструкции записываются оператором двойного (вложенного) цикла:
For i:=2 to N do { перебор уравнений системы от i=2 до i=n}
begin
R:=a[i,1]; {копирование 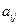 в рабочую ячейку памяти}
в рабочую ячейку памяти}
for j:=1 to N do a[i,j]:=a[i,j]-a[1,j]*R;
{пересчет всех элементов матрицы в i-ой строке}
b[i]:=b[i]-b[1]*R {пересчет значения bi}
end;
3) Преобразования, описанные в п.п.(1) и (2) следует последовательно повторить для всех остальных строк системы уравнений (1), т.е. с помощью второго уравнения исключить (обнулить) все под диагональные элементы матрицы из второго столбца, а с помощью третьего уравнения исключить все под диагональные элементы из третьего столбца и т.д.
Строгая упорядоченность выполняемых действий позволяет описать их на языке Pascal посредством вложенных циклов:
For i:=1 to N do {i- номер уравнения, которое используется для обнуления
всех коэффициентов матрицы А, расположенных в i-ом столбце
ниже главной диагонали}
begin
{выполняем пункт (1) для i-го уравнения системы}
R:=a[i,i]; {скопировали в рабочую ячейку коэффициент
матрицы на главной диагонали}
For j:=i to N do a [i,j]: = a [i,j] / R; {j-номера элементов матрицы
в i-ой строке, расположенных левее главной диагонали
Пояснение: цикл по j следует начинать именно с i, а не с 1
, т.к. все элементы матрицы в i-ой строке расположенные
левее i-ого уже обнуленными !}
b [i] : = b [i] / R; {Выполняем пункт (2) для всех уравнений систем,
расположенных ниже i-ой уравнения}
For k:=i+1 to N do {переменная k содержит номер очередного
обрабатываемого уравнения системы, из которого
исключается (обнуляется) коэффициент aki}
begin
R:=a[k,i];
For j:= i to N do a[k,j]:=a[k,j]-a[i,j]*R
{Напоминание: для j=1,2,….i-1 вычислять не надо,
т.к. там уже помещены нули}
b[k]:=b[k]-b[i]*R;
end;
end; {конец цикла по i}
Второй (завершающий) этап решения системы (1) реализуется последовательным просмотром и разрешением всех уравнений системы в обратном порядке, т.е. от N-го до первого.
Последнее уравнение системы, после проведенных преобразований имеет вид
0 ∙ 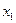 +0∙
+0∙ 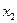 +…0∙
+…0∙ 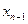 +1∙
+1∙ 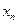 =
= 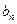 , откуда легко находим
, откуда легко находим 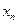 =
= 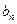 ,
,
Предпоследнее уравнение:
0∙ 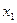 +0∙
+0∙ 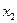 +…0
+…0 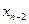 +1∙
+1∙ 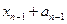 ∙
∙ 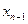 =
= 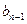
позволяет легко найти 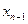 , т.к.
, т.к. 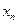 уже известно
уже известно 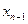 =
= 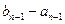 ∙
∙ 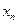
Аналогично вычисляются и все остальные искомые значения 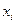 . Математически эта часть алгоритма записывается как
. Математически эта часть алгоритма записывается как
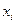 =
= 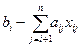 , для i = n, n-1, n-2…, 2,1
, для i = n, n-1, n-2…, 2,1
На языке Pascal:
For i:=N downto 1 do {i- номер вычисляемой неизвестной xi , который
последовательно уменьшается на 1 от величины N до 1,
i- номер окончательно разрешаемого уравнения системы}
begin
x[i]:=b[i];
for j:=i+1 to N do x[i]:= x[i]-a[i,j]*x[j]; {j – номера ранее вычисленных
значений xj}
end;
Дата добавления: 2021-12-14; просмотров: 475;











