Формулировка транспортной задачи
Оптимальное закрепление поставщиков однородного груза за потребителями, т.е. нахождение оптимальных грузопотоков, является классическим примером транспортной задачи. Эта задача возникает, когда несколько поставщиков имеют однородный груз, который в определенных объемах должен быть доставлен потребителям.
Суть транспортной задачи линейного программирования состоит в следующем. В пунктах отправления А1, А2,..., Ап имеется однородный груз в количестве а1, а2,..., ап. Этот груз необходимо доставить в пункты потребления В1, В2,..., Вт в количестве b1, b2,..., bт. Известны кратчайшие расстояния сij, между всеми пунктами отправления и получения груза. Необходимо построить план перевозок таким образом, чтобы была удовлетворена потребность в грузе всех пунктов потребления, был вывезен весь груз из пунктов производства и при минимуме транспортной работы в тонна-километрах.
Экономико-математическая модель транспортной задачи выглядит следующим образом. Система ограничений по количеству груза, доставляемого в пункты потребления:
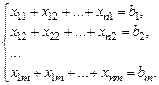
Система ограничений по количеству груза, вывозимого из каждого пункта производства:
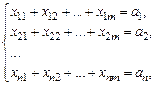
где xij – объем перевозок между i-и и j-й точками транспортной сети;
i – количество поставщиков; j – количество потребителей; аi – ограничения по предложению; bj – ограничения по спросу.
Причем предполагается, что 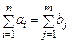 , так как это необходимо для совместимости системы уравнений. Общий объем транспортной работы (стоимости перевозок) должен быть минимальным. Поэтому целевая функция выглядит следующим образом:
, так как это необходимо для совместимости системы уравнений. Общий объем транспортной работы (стоимости перевозок) должен быть минимальным. Поэтому целевая функция выглядит следующим образом: 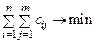 , где xij ³ 0.
, где xij ³ 0.
Математическая постановка задачи показывает, что задача закрепления поставщиков за потребителями относится к классу задач линейного программирования, называемой транспортной задачей линейного программирования. Условия транспортной задачи обычно представляются в виде матрицы, образец которой приведен в табл. 3.1.
Т а б л и ц а 3.1
Матрица условий транспортной задачи
| ГОП | ГПП | Итого | ||
| В1 | В2 | В3 | ||
| А1 | с11 | с12 | с13 | а1 |
| А2 | с21 | с22 | с23 | а2 |
| Итого | b1 | b2 | b3 |
Дата добавления: 2021-12-14; просмотров: 402;











