Задачи оптимизации и их место

в планировании перевозок

Одним из главных путей повышения эффективности работы AT является выбор из множества вариантов использования АТС оптимального, т.е. наилучшего. В зависимости от вида решаемой задачи принимается показатель, для которого стремятся найти наилучшее значение (например, минимальный пробег АТС, максимальная прибыль и т.д.). Такой показатель называется критерием оптимальности и является функцией независимых параметров (исходных данных) задачи F = F (x₁, x₂,..., х_п).

Показатели и характеристики, на значения которых наложены ограничения, являются также функциями независимых параметров и называются функциями ограничений, которые могут задаваться в виде равенств и неравенств:

R_i = R_i (х₁, х₂,..., х_n)= 0; R_i = R_i (х₁, х₂,..., х_n)£0; x_k £ 0.

Совокупность формул, позволяющая для заданного набора значений параметров х₁, х₂,..., х_n рассчитать значения функций ограничений и критерия оптимальности, называется математической моделью.

Для получения оптимальных решений применяют различные математические методы. В связи с тем, что в качестве критерия оптимальности, как правило, используют экономические показатели, такие методы носят название экономико-математических. Классификация методов, применяемых при оптимизационном планировании перевозок, представлена на рис. 3.1.

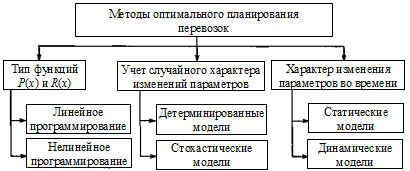
Рис. 3.1. Классификация основных методов оптимального

планирования перевозок

Линейное программирование – это математическая дисциплина, с помощью которой выполняются анализ и решение экстремальных задач с линейными связями и ограничениями. Здесь термин «программирование» является синонимом термина «планирование», т.е. подразумевается составление плана оптимального решения задачи.

Таким образом, экономическое содержание задач линейного программирования – отыскание наилучших способов использования наличных ресурсов, когда условия задачи выражаются системой линейных уравнений, содержащих неизвестные только первой степени. Многие задачи планирования грузовых автоперевозок имеют именно такое содержание. Например, закрепление грузополучателей (ГПП) за грузоотправителями (ГОП), распределение автомобилей по объектам
и маршрутам и т.д.

В математической форме общая задача линейного программирования состоит в максимизации или минимизации линейной функции

F= с₁х₁ + с₂х₂ +... + с_пх_п

от п вещественных переменных х₁, х₂,..., х_п ,удовлетворяющих условиям неотрицательности (х₁ > 0, х₂> 0,..., х_п > 0) и т линейным ограничениям

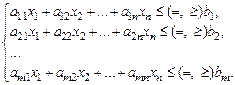
Среди ограничений могут одновременно встречаться знаки «³», «£» и «=». Значения с_i, а_ij, b_j предполагаются известными.

К математическому программированию относятся также и методы нелинейного программирования. Соответствующие задачи в этом случае описываются нелинейными уравнениями. Для решения задач, относящихся к классу задач нелинейного программирования, приходится применять сложные алгоритмы, на практике реализуемые только при помощи ЭВМ.

Некоторые задачи планирования грузовых автоперевозок связаны
с принятием ряда последовательных и поэтапных решений. Для решения таких задач используются методы динамического программирования, в основе которых лежит совокупность приемов, позволяющих находить оптимальные решения, основанные на вычислении последствий каждого из принятых решений и выработке оптимальных стратегий для последующего решения.

В решении планово-экономических задач находят также применение методы, базирующиеся на теории вероятностей, математической статистике и теории массового обслуживания. При построении стохастических моделей исходят из вероятностной трактовки экономического процесса и его параметров. При этом каждой входящей в модель величине приписывается не одно какое-либо число, а указывается вероятностный закон распределения значений этой величины и характеристики этого распределения (математическое ожидание, дисперсия и т.д.).