Математические знания

В рассматриваемую эпоху математические знания развивались в следующих основных направлениях.

Во-первых, расширяются пределы считаемых предметов, появляются словесные обозначения для чисел свыше 100 единиц — сначала до 1000, а затем вплоть до 10 000.

В о - в т о р ы х, закладываются предпосылки позиционной системе исчисления. Они состояли в совершенствовании умения считать не единицами, а сразу некоторым набором единиц (4, 5, чаще всего 10). Когда нужно было пересчитать большое количество одинаковых предметов (например, стадо скота), применялся так называемый групповой счет. Такой счет вело несколько человек: один — вел счет единицам, второй — десяткам, третий — сотням (наблюдения Н.Н. Миклухо-Маклая *). Развитие хозяйства, торговли требовало не просто умения считать, но и умения сохранять на длительное время или передавать на расстояния результаты счета (очень часто — боль­ше числа). Для этого применялись известные еще с древнейших времен бирки, шнуры, нарезки или узлы, на которых уже обозначаются не только единицы, но и группы единиц (по 4, 5,10,20 единиц). По сути, формировался прообраз различных систем счисления.

*' См.: Миклухо-Маклай Н.Н. Собр. соч. М.; Л., 1950. Т. 1. С. 141.

В-третьих, формируются простейшие геометрические абстракции — прямой линии, угла, объема и др. Развитие земледелия, отношений земельной собственности требуют умения измерять расстояния, площади земельных участков (отсюда и происхождение слова «геометрия» — от древнегреческого «землемерие»). Развитие строительного дела, гончарного производства, распределение урожая зерновых и проч. требовало умения определять объемы тел. В строительстве было необходимо уметь проводить прямые горизонтальные и вертикальные линии, строить прямые углы и т.д. Натянутая веревка служила прообразом представления о геометрической прямой линии. Одним из важнейших свидетельств освоения человеком геометрических абстракций является зафиксированный археологами бурный всплеск использования геометрических орнаментов на сосудах, ткани, одежде. Геометрическая отвлеченность начинает превалировать в художественной изобразительной деятельности, в передаче изображений животных, растений, человека.

На Древнем Востоке математика получила особое развитие в Ме­сопотамии. Математика развивалась как средство решения повсе­дневных практических задач, возникавших в царских храмовых хо­зяйствах (землемерие, вычисление объемов строительных и земля­ных работ, распределение продуктов между большим числом людей и др.). Найдено более сотни клинописных математических текстов, которые относятся к эпохе Древневавилонского царства (1894— 1595 гг. до н.э.). Их расшифровка (Варден ван дер Б.Л. и др.) показа­ла, что в то время уже были освоены операции умножения, определе­ния обратных величин, квадратов и кубов чисел, существовали таб­лицы с типичными задачами на вычисление, которые заучивали наи­зусть *. Математики Древнего Вавилона уже оперировали позиционной системой счисления (в которой цифра имеет разное значение в зависимости от занимаемого ею места в составе числа). Система счисления была шестидесятиричной. Жителям Древнего Вавилона были известны приближенные значения отношения диаго­нали квадрата к его стороне они считали равным приблизительно 1,24; число π — приблизительно равным 3,125).

* См.: Варден ван дер Б.Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. М., 1959; Рыбников К.А. История математики. 2-е изд. М., 1974; и др.

Вавилонская математика поднялась до алгебраического уровня, оперируя не числом конкретных предметов (людей, скота, камней и проч.), а числом вообще, числом как абстракцией. При этом числа рассматривались как некий символ иной, высшей реальности (наряду с множеством других символов такой высшей реальности). Но у древ­них вавилонян, по-видимому, еще не было свойственного древнегре­ческой математике представления о числах как некоторой абстракт­ной реальности, находящейся в особой связи с материальным миром. Поэтому у них не вызывали мировоззренческих проблем вопросы о природе несоизмеримых отношений и иррациональных чисел.

На современном математическом языке те типовые задачи, кото­рые могли решать вавилоняне, выглядят следующим образом:

Алгебра и арифметика:

уравнения с одним неизвестным

АХ =B; X²= А; X² + АХ = В; X² - АХ = В; X³ = А; X²(X + 1)=А;

системы уравнений с двумя неизвестными

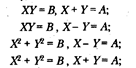
им были известны следующие формулы:

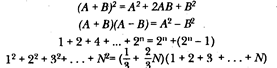
и суммирование арифметических прогрессии.

Геометрия:

пропорциональность для параллельных прямых;

теорема Пифагора;

площадь треугольника и трапеции;

площадь круга == 3R²;

длина окружности == 6R;

объем призмы и цилиндра;

объем усеченного конуса они считали по неправильной формуле: 1/2 (ЗR² + Зr²) (на самом деле он равен 1/3(R² - r²).

Объем усеченной пирамиды с высотой Н, квадратным верхним В) и нижним (А) основаниями они определяли по неправильной формуле: 1/2 (А² + В²)Н; на самом деле он равен 1/3(А² + АВ+ В²)Н.

Основная общая особенность и общий исторический недостаток древневосточной математики — ее преимущественно рецептурный, алгоритмический, вычислительный характер. Математики Древнего Вocтока даже не пытались доказывать истинность тех вычислительных формул, которые они использовали для решения конкретных фактических задач. Все такие формулы строились в виде предписаний: «делай так-то и так-то». Потому и обучение математике состояло в механическом зазубривании и заучивании веками не изменявшихся пособов решения типовых задач. Идеи математического доказательства в древневосточной математике еще не было.

Вместе с тем у древних вавилонян уже складывались отдельные предпосылки становления математического доказательства. Они состояли в процедуре сведения сложных математических задач к прошлым (типовым) задачам, а также в таком подборе задач, который позволял осуществлять проверку правильности решения.