Закон Фитса и закон Хика

Основы знаний надлежит искать в математике.
Роджер Бэкон «Opus Majus», XIII в.

Различные количественные законы, имеющие отношение к разработке интерфейсов, имеют хорошее когнитивное обоснование, и их правильность была неоднократно проверена. Эти законы часто дают нам дополнительные данные, на основе которых можно принимать те или иные решения, связанные с разработкой интерфейсов. Закон Фитса (Fitts' Law) позволяет определить количественно тот факт, что чем дальше находится объект от текущей позиции курсора или чем меньше размеры этого объекта, тем больше времени потребуется пользователю для перемещения к нему курсора. Закон Хика (Hick's Law) позволяет количественно определить наблюдение, заключающееся в том, что чем больше количество вариантов заданного типа вы предоставляете, тем больше времени требуется на выбор.

Закон Фитса

Представим, что вы перемещаете курсор к кнопке, изображенной на экране. Кнопка является целью данного перемещения. Длина прямой линии, соединяющей начальную позицию курсора и ближайшую точку целевого объекта, определяется в законе Фитса как дистанция. На основе данных о размерах объекта и дистанции закон Фитса позволяет найти среднее время, за которое пользователь сможет переместить курсор к кнопке.

В одномерном случае, при котором размер объекта вдоль линии перемещения курсора обозначается как S, а дистанция от начальной позиции курсора до объекта — как D (рис. 4.6), закон Фитса формулируется следующим образом:

Время (мс) = a + b \log_2(D/S+1)

(Константы a и b устанавливаются опытным путем по параметрам производительности человека.)²⁶

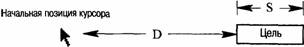
Расстояния, которые используются в законе Фитса для определения времени, необходимого для перемещения курсора к цели

Вычисляемое время отсчитывается от момента, когда курсор начинает движение по прямой линии, до момента, когда пользователь щелкает мышью по целевому объекту. Логарифм по основанию 2 является мерой трудности задачи в количестве бит информации, которое требуется для описания (одномерного) пути перемещения курсора.

Для вычисления времени можно использовать любые единицы измерения дистанции, т.к. D/S является отношением двух дистанций и поэтому не зависит от единицы измерения. Отсюда следует, что хотя указательное устройство может переместиться на расстояние большее или меньшее, чем то расстояние, на которое переместится на экране курсор, закон все равно работает, при условии, что соотношение между движением ГУВ и курсора является линейным. Закон Фитса может применяться только к тем типам перемещения, которые совершаются при использовании большинства человеко-машинных интерфейсов, т.е. к таким перемещениям, которые невелики относительно размеров человеческого тела и которые являются непрерывными (совершаемыми одним движением). Для приближенных вычислений я использую следующие значения констант в уравнении закона Фитса: a=50, b=150.

Также проводились тестирования с законом Фитса, дополненным некоторыми более сложными параметрами, такими, например, как перемещение курсора между прямыми или искривленными границами (Accot и Zhai, 1997). Для двумерных целей обычно можно получить корректное приближенное значение времени, необходимого для перемещения курсора к объекту, используя в качестве параметра S наименьшее из значений размеров объекта по горизонтали или по вертикали (Mackenzie, 1995).

Меню в Macintosh, расположенное у верхней границы экрана, увеличивается в размере, что является более эффективным по сравнению с меню, которое всплывает из-за границы экрана

Закон Фитса позволяет объяснить, например, почему переместить курсор к меню в стиле Apple Macintosh, располагающемуся на границе экрана намного быстрее, чем переместить курсор к меню в стиле Microsoft Windows, которое всплывает из-за границы экрана (рис. 4.8). Размер S меню в Windows на моем экране составляет 5 мм. Эффективный размер меню в Macintosh является довольно большим, потому что пользователю не требуется останавливаться в пределах полосы меню; он может просто передвинуть ГУВ на любое расстояние превышающее расстояние, необходимое для размещения курсора в пределах меню, — курсор в любом случае остановится на границе экрана.

Меню в Windows находится под верхней границей экрана, поэтому пользователю нужно более точно подводить курсор к меню, чтобы, можно было вызвать подменю

Ряд выполненных мной тестов помог установить, что пользователи Macintosh обычно останавливаются в пределах 50 мм от границы экрана, поэтому для Macintosh мы можем принять 50 мм как S. При использовании 14-дюймового плоского монитора среднее расстояние, на которое требуется переместить курсор, чтобы достичь панели меню, составляет 80 мм. Таким образом, время перемещения курсора к какому-либо из элементов меню в Macintosh будет:

50 + 150 \log_2(80/50+1) = 256 мс

Это время является намного меньшим, чем то, которое требуется на перемещение курсора к необходимому элементу меню в Windows:

50 + 150 \log_2(80/5+1) = 663 мс

Полученные значения времени относятся только лишь к перемещению курсора. Щелчок по целевому объекту, к которому перемещался курсор, добавляет в среднем еще 0.1 с. (Значение оператора K=0.2, принятое в модели GOMS, учитывает и нажатие кнопки, и ее отпускание, в то время как указанное значение учитывает только нажатие кнопки.) При проведении обычного эксперимента вам придется добавить еще 0.25 с, чтобы учесть время человеческой реакции в начале движения курсора. С учетом всех этих факторов мы получим именно те значения, которые я получил экспериментальным путем: в среднем пользователю требуется около 0.6 с, чтобы открыть Apple-меню, в то время как для открытия Windows-меню требуется более 1 с. Таким образом, этот анализ объясняет, почему при разработке интерфейса Macintosh меню были намеренно помещены на границе экрана.

Закон Хика

Перед тем как переместить курсор к цели или совершить любое другое действие из набора множества вариантов, пользователь должен выбрать этот объект или действие. В законе Хика утверждается, что когда необходимо сделать выбор из n вариантов, время на выбор одного из них будет пропорционально логарифму по основанию 2 от числа вариантов плюс 1, при условии, что все варианты являются равновероятными. В этом виде закон Хика очень похож на закон Фитса:

Время (мс) = a + b \log_2(n+1)

Если вероятность 1-го варианта равна p(i), то вместо логарифмического коэффициента используется

\sum_i p(i) \log_2(1/p(i)+1)

Коэффициенты, используемые в выражении закона Хика, в большой степени зависят от многих условий, включая то, как представлены возможные варианты, и то, насколько хорошо пользователь знаком с системой. (Если варианты представлены непонятным образом, значения a и b возрастают. Наличие навыков и привычек в использовании системы снижает значение b.) Мы не будем рассматривать эти зависимости — для нас важно, что для принятия того или иного решения требуется время; что для принятия сложных решений требуется больше времени, чем для принятия простых решений; и что взаимосвязь является логарифмической. При отсутствии более точных данных для проведения быстрых и приблизительных вычислений мы можем воспользоваться теми же значениями a и b, которые использовали для закона Фитса.

При использовании любых положительных и ненулевых значений a и b из закона Хика следует, что предоставление пользователю сразу нескольких вариантов одновременно обычно является более эффективным, чем организация тех же вариантов в иерархические группы. Выбор из одного меню, состоящего из 8 элементов, производится быстрее, чем из двух меню, состоящих их 4 элементов каждое. Если все элементы могут быть выбраны с равной вероятностью и если не учитывать время, необходимое для открытия второго меню (которое, конечно, еще более увеличило бы время для интерфейса, состоящего из двух меню), то сравнение времени для выбора одного элемента из восьми (a + b \log_2 8) с удвоенным временем для выбора одного элемента из четырех 2 (a + b \log_2 4) покажет, что

а + 3b < 2(а + 2b)

поскольку \log_2 8 = 3, a \log_2 4 = 2, а также поскольку a<2a и 3b<4b.

Это согласуется с данными, полученными в экспериментах со структурами меню (см. например, Norman и Chin, 1988).

Наше рассмотрение законов Фитса и Хика нельзя считать полным. Например, следует обратить внимание на то, что эти законы не случайно принимают ту же форму, что и теорема Шэннона — Хартли (Shannon-Hartley). Тем не менее, этого короткого рассмотрения вполне достаточно для того, чтобы отметить их ценность с точки зрения разработки интерфейсов. Они могут быть полезными даже в том случае, когда эмпирические значения коэффициентов a и b не известны (как это было в нашем примере). (Более подробные сведения см. в Card, Moran и Newell, 1983, с. 72-74.)