Понятие векторов и операции над ними.

Определение.Отрезок, имеющий заданные длину и направление в пространстве называется вектором.

A

O

Определение.Два вектора считаются равными, если выполнены условия:

а) длины векторов равны;

б) векторы коллинеарны, (т. е. расположены на одной прямой или на параллельных прямых);

в) векторы имеют одинаковое направление.

Следует различать начало и конец вектора. Поменяв их местами, мы получим уже другой вектор, направленный противоположно исходному.

А О

О А

Из определения равенства векторов следует, что при параллельном переносе вектора получаем вектор, равный исходному. Поэтому начало вектора можно помещать в любой точке пространства. Вектор с началом в точке O и концом в точке M обозначим символом 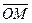или 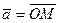. Длину вектора 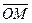обозначим | 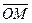| или | 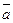|. Вектор, у которого начало совпадает с концом, называется нулевым вектором.

Определение.Два вектора, 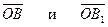, имеющие равные длины, но противоположно направленные, называются противоположными векторами. Сумма их равна нулевому вектору.

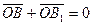
B O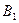

Вектор противоположный вектору 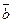будем обозначать .

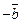Определение. Суммой векторов 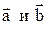называется такой вектор , начало которого совпадает с началом вектора 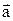, а конец – с началом вектора 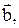при условии, что начало вектора 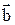перенесено в конец вектора 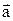(правило треугольника).

Пример 1. Таким образом, чтобы сложить два вектора 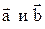, нужно выбрать на плоскости произвольную точку М и отложить от нее вектор

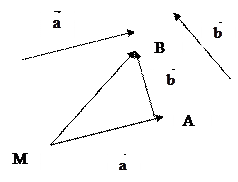
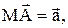а затем от точки А отложить вектор 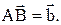Тогда вектор 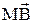является суммой векторов 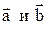, т.е.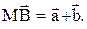

Суммой двух векторов 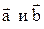является диагональ параллелограмма, построенного на этих векторах, исходящая из их общего начала (правило параллелограмма).

Пример 2. Сложить векторы 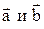, пользуясь правилом параллелограмма.

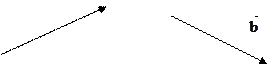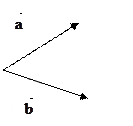
Возьмем произвольную точку О на плоскости. Отложим от нее вектор 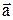и вектор 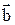(приведем их к общему началу).

Построим на этих векторах параллелограмм.

Тогда суммой векторов 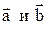будет вектор 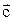, являющийся диагональю параллелограмма и выходящий из общего начала векторов 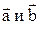, т.е. .

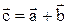Отсюда сразу следует, что .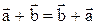

Сложение многих векторов производится при помощи последовательного применения правила треугольника.

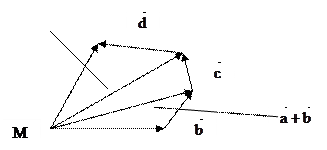
Пример 3. Найти сумму векторов .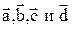

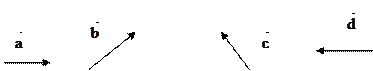Возьмем произвольную точку М на плоскости и отложим от нее вектор 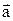, затем от конца вектора 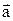отложим вектор 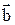; от конца вектора 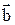отложим вектор ; от конца вектора отложим вектор 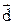. Соединяя начало вектора 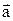с концом вектора 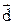, получим результирующий вектор, являющийся суммой данных четырех векторов.

Определение. Разностью векторов 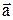и 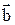называют сумму вектора 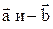, т.е. .

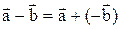Если два вектора 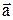и 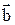приведены к общему началу, то их разность 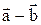есть вектор, идущий из конца 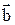("вычитаемого") к концу 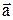("уменьшаемого").

Пример 4. Найти разность векторов 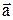и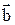

Возьмем произвольную точку М на плоскости и отложим от нее векторы и

Соединим концы векторов и направим этот отрезок из конца в конец 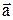. Этот вектор и будет разностью векторов 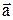и .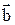

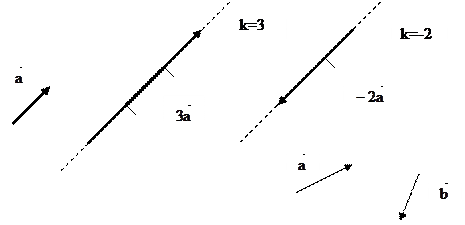
Определение. Произведениемвектора 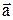на число (скаляр) k называется вектор 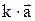, который имеет длину, равную 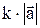и коллинеарен 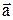. При этом, если k>0, то векторы 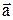и 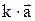сонаправлены, если k<0, то они противоположно направлены.

Пример. Даны векторы 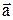и :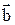

Построить вектор .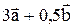

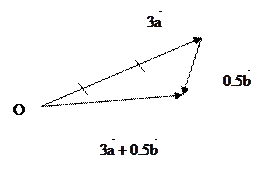Возьмем произвольную точку О на плоскости. Отложим от нее 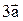, а затем от конца полученного вектора отложим 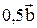. Теперь соединим точку О с концом вектора 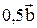. Полученный вектор и будет результирующим.