Активно-емкостная нагрузка
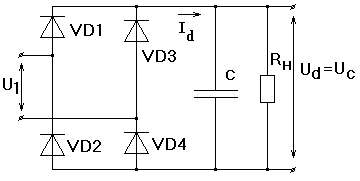 |
Рассмотрим влияние активно-емкостной нагрузки на примере работы однофазного мостового выпрямителя.
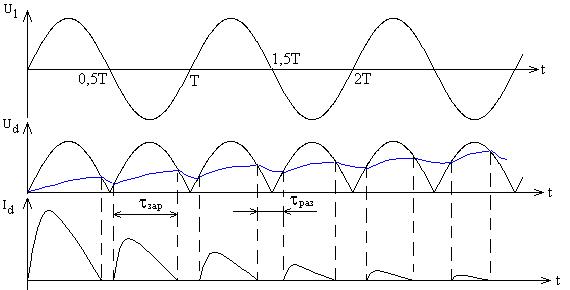 |
На рисунке представлены графические зависимости токов и напряжений, поясняющие переходные процессы в схеме в момент подключения выпрямителя к источнику U1.
На интервале tзар U1>UС и при этом происходит заряд емкости C сглаживающего фильтра через внутреннее сопротивление выпрямительного звена. При этом появляется большой импульсный ток, значения которого в 20…40 раз выше установившегося значения средневыпрямленного тока вентиля. Особенно это выражено в источниках питания с бестрансформаторным входом. Для ограничения этого тока вводят резисторы, терморезисторы или резисторы шунтированные управляемыми ключами, выполненные на симисторах, тиристорах или динисторах. Ключи позволяют с учетом времени установления переходного процесса производить ограничение тока только в момент пуска источника питания, следовательно, повышаются КПД и надежность выпрямителя.
На интервале tраз, когда напряжение на емкости уравнивается с напряжением источника, конденсатор разряжается на нагрузку. С увеличением тока нагрузки увеличивается уровень пульсации выпрямленного напряжения из- за уменьшения постоянной цепи разряда tраз =RНС. При этом ухудшаются сглаживающие действия фильтра.
При расчете выпрямителя с емкостной нагрузкой используют метод Терентьева – метод номограмм. Он основан на расчете вспомогательных коэффициентов зависящих от угла протекания тока через вентиль. Вводят коэффициент А=f(q), где q - угол протекания тока через вентиль. Для различных схем выпрямителей приводятся номограммы, которые получены экспериментальным путем для различных мощностей и схем выпрямителей. Расчет параметров Uобр, Iаср, Iад, U2, I2 выполняют через вспомогательные коэффициенты: В, С, D=f(A). Для получения связи среднего тока через вентиль с параметром А проведем интегрирование на интервале q. При выводе соотношения примем емкость конденсатора, близкую к бесконечности (СÞ¥ ), а пороговое напряжение диода равным нулю. Для получения среднего значения тока через вентиль переместим оси координат в середину импульса тока и воспользуемся уравнением для среднего значения тока:  (1)
(1)
 ,
, 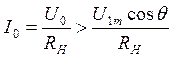 (2).
(2).
Нижеприведенные диаграммы поясняют вывод соотношений для Ud.
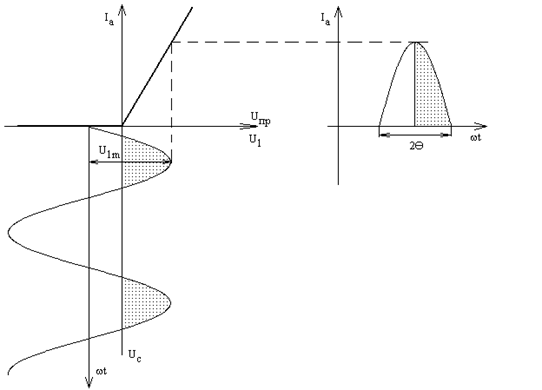
На интервале 2q ток вентиля совпадает с током нагрузки. Приравняем (1) и (2) и поделим внутреннюю скобку в выражении (1) на cosq, получим: 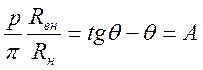 .
.
Дата добавления: 2018-05-10; просмотров: 1680;











