Предел ограниченной последовательности

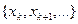Рассмотрим ограниченную последовательность чисел . Последовательность также ограничена при любом 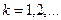. Построим две числовые последовательност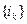и и :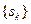

, .

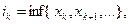
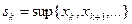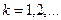Свойства последовательносте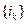й и :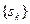

1. ,

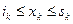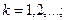
2. 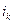— неубывающая последовательность;

3. 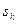— невозрастающая последовательность.

Первое свойство следует из определения чисел 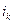и 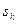. Так как множество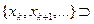 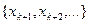, то второе и третье свойства вытекают из теоремы 1.7.

Из свойств 1––3 следует цепочка неравенств

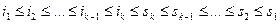. (3.1)

Таким образом, последовательность 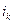— неубывающая и ограниченная сверху числом 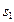, а последовательность 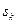— невозрастающая и ограниченная снизу числом 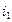. Введем обозначения:

, .

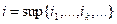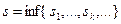Числа 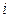и 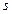называются соответственно нижним и верхним пределом последовательности .

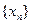Теорема 2.3.Справедливы следующие утверждения.

1.Нижний предел последовательности не превосходит ее верхний предел, т.е. .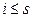

2.Для каждого 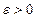неравенство 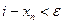справедливо при всех .

3.Для каждого 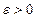неравенство 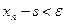справедливо при всех .

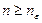Доказательство

1.Действительно, из условия (3.1) следует, что 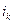при любом 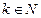является нижней гранью множества 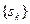. Так как 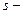наибольшая нижняя грань этого множества, то 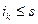при любом 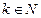. Отсюда следует, что 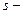верхняя грань множества 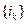. Ввиду того, что 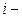наименьшая верхняя грань множества 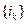, то .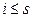

2.Так как число 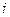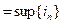, тоиз свойства точной верхней грани неубывающей последовательности следует, для каждого 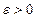неравенство

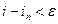(3.2)

справедливо при всех . Из первого свойства последовательности 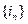вытекает 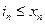при всех 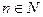. Отсюда и из неравенства (3.2) следует, что при всех 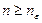справедливы неравенства:

.

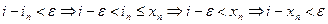3.Так как число 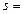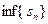, тоиз свойства точной нижней грани невозрастающей последовательности следует, для каждого 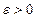неравенство

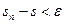(3.3)

справедливо при всех 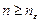. Из первого свойства последовательности 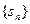вытекает 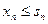при всех 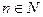. Отсюда и из неравенства (3.3) следует, что при всех 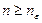справедливы неравенства

. ■

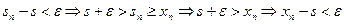Если для ограниченной последовательности нижний и верхний пределы совпадают, т.е. 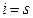, то последовательность называется сходящейся, а число 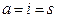называется пределом последовательности . Неограниченная последовательность предела не имеет.

Если число является пределом последовательности , то будем говорить, что она сходится к числу и писать 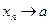. Предел последовательности обозначают символом 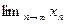, т.е. 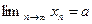. Если последовательность не имеет предела, то ее называют расходящейся. Неограниченная последовательность является расходящейся.

Примеры

3.1. Найти предел последовательности , .

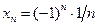Решение. Последовательность 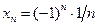имеет вид:

.

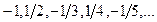Так как 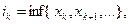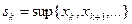, , 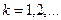то

.

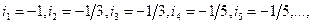
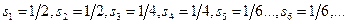Неубывающая последовательность 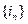ограничена сверху числом 0 и 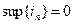. Невозрастающая последовательность 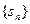ограничена снизу числом 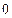и 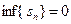. Итак, 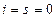, поэтому .

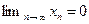3.2. Последовательность , , 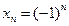предела не имеет.

Решение. Имеем:

;

.

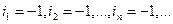
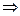
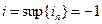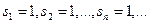
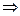
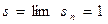Так как 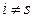, то последовательность , , 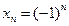предела не имеет.●

Теорема 2.4. Следующие утверждения справедливы.

1. Неубывающая или возрастающая последовательность , ограниченная сверху, сходится, и число 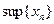является ее пределом.

2.Невозрастающая или убывающая последовательность , ограниченная снизу, сходится, и число 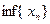является ее пределом.

Доказательство.

1.Так как 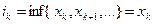; 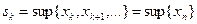, то последовательность 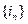совпадает с исходной последовательностью , а последовательность является стационарной, каждый член которой равен 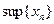. Отсюда находим: 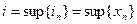, 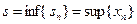. Значит, последовательность сходится, и .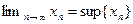

2.Доказательство проводится аналогично предыдущему пункту. ■

Примеры

3.3. Предел стационарной последовательности , 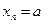при любом 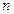, равен .

Решение. Стационарная последовательность является неубывающей, поэтому ее предел равен .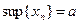

3.4. Найти предел последовательности , где , .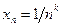

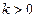Решение. Последовательность убывающая:

,

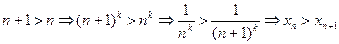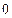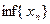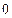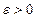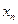
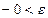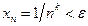
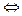
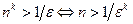и ограниченная снизу числом , поэтому ее предел равен . Докажем, что число является точной нижней гранью последовательности , т.е. для каждого неравенство справедливо при всех (свойство 2 в § 2.2). Имеем: . Из теоремы 2.1 следует, что неравенство 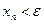справедливо при всех . ●

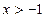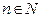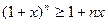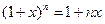
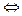
Лемма(Бернулли).Если , то при любом справедливо неравенство , причем 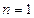, или .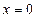

Доказательство.Ес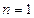ли , или 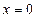, то верно 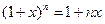. Если же 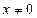и 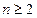, то доказательство неравенства проведем методом математической индукции.

Утверждение леммы справедливо, если :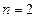

.

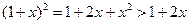Докажем, что из истинности неравенства 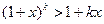, следует справедливость неравенства :

. ■

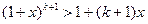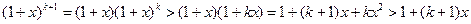Число e. Числовая последовательность 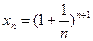сходится.

Докажем, что последовательность убывает и ограничена снизу. Используя лемму Бернулли, имеем

, .

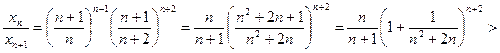
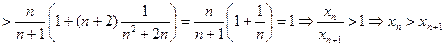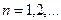Этим доказано, что последовательность 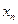убывает. Так как 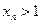, то последовательность 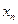ограничена снизу. Следовательно, эта последовательность имеет предел. Предел последовательности 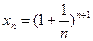равен числу . ■

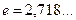§ 2.4. Критерий сходимости последовательности

Находить предел последовательности, используя его определение,— достаточно трудоемкий процесс. Поэтому, построим инструменты, при помощи которых будут сформулированы приемы и методы нахождения пределов значительного числа последовательностей.

Теорема 2.5. Следующие условия равносильны.

1. Число является пределом ограниченной последовательности .

2. Для каждого числа 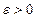неравенство 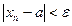справедливо при всех 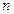, начиная с некоторого номера, т.е. при всех 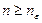, где 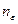некоторое натуральное число.

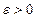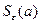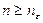3. Для каждого числа окрестность точки содержит члены последовательности при всех , где 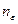некоторое натуральное число.

1 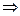2.Пусть 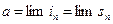и 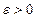— произвольное положительное число. Тогда из теоремы 2.3 получаем :

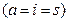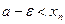, если 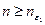; 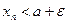, если .

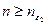Если 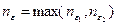, то 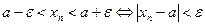, если .

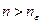2 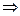3.Расстояние между точками 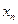и равно 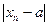. Следовательно, из условия 2следует, что для каждого положительного числа 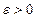все точки последовательности находятся от точки на расстоянии меньше 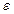при всех 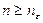, т.е. 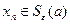при всех .

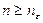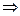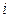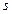3 1.Из условия 3 теоремы 2.5 и теоремы 2.1 следует ограниченность последовательности . Следовательно, существуют числа и . Докажем, что .

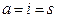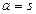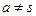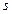Сначала методом от противного докажем, что . Пусть и расстояния между точками и равно 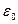, т.е. 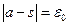Возьмем 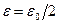. Из условия 3 теоремы: 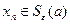при любом 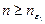. Отсюда следует, что неравенство 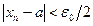справедливо при любом .

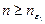Из свойства числа 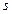вытекает, что неравенство 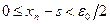справедливо при всех 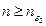. Полагаем 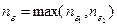. Тогда при всех имеем:

.

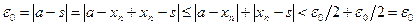Противоречие. Аналогично доказывается равенство . ■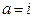

Следствие. Если последовательность 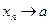и число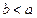 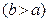, то неравенство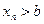 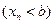будет выполняться для всех .

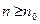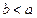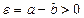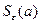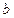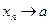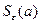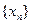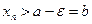Доказательство.Рассмотрим случай . Возьмем число . Каждое число из окрестности больше числа . Так как последовательность , то в окрестность попадают все члены последовательности , если (условие 3 теоремы), т.е. для всех 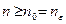. Аналогично рассматривается случай . ■

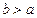Замечание. Еслидля каждого числа 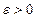неравенство 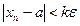, , 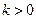справедливо при всех 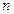, начиная с некоторого номера, то .

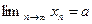Доказательство.Возьмем произвольное 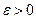. Так как 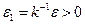, то неравенство 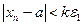будет справедливо при всех 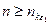. Отсюда, ввиду 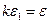, следует справедливость неравенства 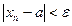при всех 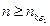, поэтому .▲

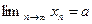Теорема 2.5 не содержит указаний для нахождения предела последовательности, но она формулирует условия, при помощи которых можно получить ответ на вопрос: число является пределом последовательности ?

§ 2.5. Связь пределов последовательности и ее