ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
§2.1. Числовые последовательности
Если каждому натуральному числу 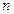 поставлено в соответствие действительное число
поставлено в соответствие действительное число 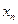 :
:
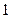 ,
, 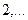 ,
, 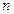 ,…
,…
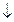
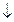 …
… 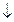
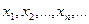 ,
,
то говорят, что задана числовая последовательность 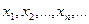 . Другими словами, числовая последовательность — это действительные числа, занумерованные всеми натуральными числами и расположенные в порядке возрастания номеров. Эти действительные числа называются членами или элементами последовательности. Элемент
. Другими словами, числовая последовательность — это действительные числа, занумерованные всеми натуральными числами и расположенные в порядке возрастания номеров. Эти действительные числа называются членами или элементами последовательности. Элемент 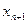 следует за элементом
следует за элементом 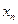 , а
, а 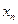 предшествует элементу
предшествует элементу 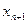 . Числовую последовательность будем кратко обозначать символом
. Числовую последовательность будем кратко обозначать символом  .
.
Число 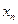 называют общим или
называют общим или 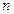 -м членом последовательности. Числовая последовательность считается заданной, если указан метод вычисления общего члена
-м членом последовательности. Числовая последовательность считается заданной, если указан метод вычисления общего члена 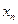 при каждом значении
при каждом значении 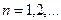 . Чаще всего указывается формула для общего члена
. Чаще всего указывается формула для общего члена 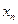 последовательности, используя которую вычисляют члены последовательности.
последовательности, используя которую вычисляют члены последовательности.
Примеры
1.2. Числовая последовательность задана формулой:
a) 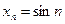 ; б)
; б) 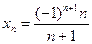 .
.
Написать ряд элементов этих последовательностей.
Решение.Подставляя в общий член последовательности вместо 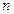 натуральные числа
натуральные числа 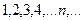 , получим:
, получим:
a) 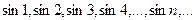 ; б)
; б) 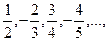
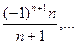 ●
●
Рассмотрим числовую последовательность  и некоторую окрестность точки
и некоторую окрестность точки  —
— 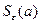 . Далее будет часто встречаться ситуация, когда все члены последовательности
. Далее будет часто встречаться ситуация, когда все члены последовательности  , кроме конечного числа, будут принадлежать этой окрестности.
, кроме конечного числа, будут принадлежать этой окрестности.
Замечание. Следующие условия равносильны:
1. Окрестности 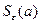 принадлежат все члены последовательности
принадлежат все члены последовательности  , кроме конечного числа, т.е. вне окрестности
, кроме конечного числа, т.е. вне окрестности 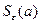 находится лишь конечное число членов последовательности
находится лишь конечное число членов последовательности  .
.
2. При всех  члены последовательности
члены последовательности  принадлежат окрестности
принадлежат окрестности 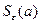 , где
, где 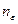 — некоторое натуральное число.
— некоторое натуральное число.
3. Неравенство 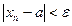 справедливо при всех
справедливо при всех  , где
, где 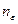 — некоторое натуральное число.
— некоторое натуральное число.
Доказательство
1 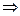 2.Вне окрестности
2.Вне окрестности 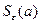 находится лишь конечное число членов последовательности
находится лишь конечное число членов последовательности  :
: 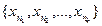 Обозначим через
Обозначим через 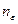 любое число, которое больше чисел
любое число, которое больше чисел 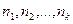 . Тогда все члены последовательности, номера которых
. Тогда все члены последовательности, номера которых  принадлежат окрестности
принадлежат окрестности 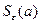 .
.
2 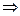 3.При всех
3.При всех  справедлива цепочка импликаций:
справедлива цепочка импликаций:
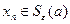
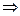
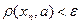
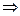
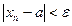 .
.
3 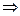 1. При всех
1. При всех  справедлива цепочка импликаций:
справедлива цепочка импликаций:
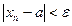
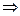
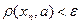
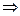
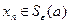 .
.
Отсюда следует, что только члены последовательности 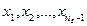 могут не принадлежать окрестности
могут не принадлежать окрестности 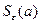 , т.е. вне окрестности
, т.е. вне окрестности 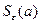 находится лишь конечное число членов последовательности
находится лишь конечное число членов последовательности  .▲
.▲
Числовая последовательность является числовым множеством, поэтому можно говорить о верхней и нижней грани последовательности. Отсюда следует, что:
а) последовательность  ограничена, если
ограничена, если 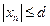 для любого
для любого 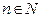 ;
;
б) последовательность  неограничена, если для любого
неограничена, если для любого 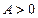 найдется элемент
найдется элемент 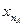 этой последовательности, для которого
этой последовательности, для которого 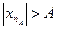 .
.
Теорема 2.1. Справедливы следующие утверждения.
1. Если интервал 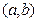 содержит все члены последовательности
содержит все члены последовательности  , начиная с некоторого номера
, начиная с некоторого номера 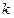 , то эта последовательность является ограниченной.
, то эта последовательность является ограниченной.
2. Если при каждом 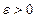 равносильны неравенства:
равносильны неравенства:
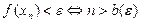 ,
,
где 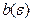 — число, не зависящее от номера
— число, не зависящее от номера 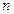 , то неравенство
, то неравенство 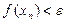 справедливо при всех
справедливо при всех  .
.
3. Если неравенство 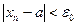 справедливо для всех членов последовательности с номерами
справедливо для всех членов последовательности с номерами 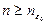 , то неравенство
, то неравенство 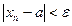 справедливо при всех
справедливо при всех 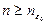 и при любом
и при любом 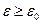 .
.
Доказательство
1.Интервал 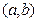 содержит все члены последовательности
содержит все члены последовательности  , кроме членов
, кроме членов 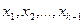 . Число
. Число 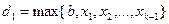 является верхней гранью последовательности
является верхней гранью последовательности  , а число
, а число 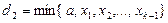 — нижняя грань последовательности
— нижняя грань последовательности  . Следовательно, последовательность
. Следовательно, последовательность  ограничена.
ограничена.
2. Неравенство 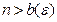 справедливо при всех
справедливо при всех  , где
, где 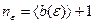 (число
(число 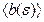 равно
равно 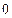 , если
, если 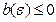 ; если же
; если же 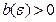 , то
, то 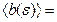
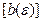 ). Следовательно, неравенство
). Следовательно, неравенство 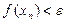 справедливо при всех
справедливо при всех  .
.
3.Если неравенство 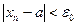 справедливо для всех членов последовательности с номерами
справедливо для всех членов последовательности с номерами 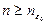 , то неравенство
, то неравенство 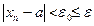 также справедливо при всех
также справедливо при всех 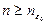 .■
.■
В последовательности  выберем элемент, номер которого обозначим символом
выберем элемент, номер которого обозначим символом 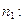
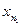 . Затем выберем другой элемент —
. Затем выберем другой элемент — 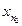 , номер
, номер 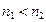 , и так далее. Получим последовательность элементов
, и так далее. Получим последовательность элементов
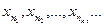 , причем
, причем 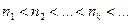 ,
,
которая называется подпоследовательностью последовательности  и обозначается символом
и обозначается символом 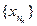 . Заметим, что в последовательности
. Заметим, что в последовательности 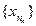 номером члена
номером члена 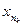 является число
является число 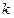 , а
, а 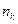 — его номер в последовательности
— его номер в последовательности  . Члены подпоследовательности
. Члены подпоследовательности 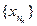 можно обозначить новыми буквами:
можно обозначить новыми буквами:
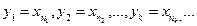 .
.
Иными словами, подпоследовательность — это бесконечная часть последовательности, в которой следование одного элемента за другим остается таким же, как и в исходной последовательности. Например, последовательности 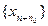 ,
, 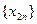 ,
, 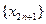 являются подпоследовательностями последовательности
являются подпоследовательностями последовательности  .
.
Чтобы доказать, что последовательность 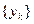 является подпоследовательностью последовательности
является подпоследовательностью последовательности  надо установить, что а) каждый элемент
надо установить, что а) каждый элемент 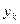 является членом последовательности
является членом последовательности  , т.е.
, т.е. 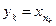 , б)
, б) 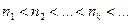 .
.
Примеры
1.2. Доказать, что последовательность 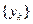 ,
, 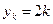 , является подпоследовательностью последовательности
, является подпоследовательностью последовательности  ,
, 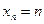 .
.
Решение. Так как 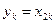 , то
, то 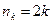 , и
, и 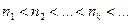 , поэтому последовательность
, поэтому последовательность 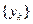 является подпоследовательностью последовательности
является подпоследовательностью последовательности  .
.
1.3. Доказать, что последовательность 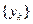 ,
, 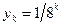 , является подпоследовательностью последовательности
, является подпоследовательностью последовательности  ,
, 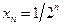 .
.
Решение. Так как 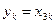 , то
, то 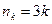 , и
, и 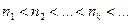 , поэтому последовательность
, поэтому последовательность 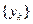 является подпоследовательностью последовательности
является подпоследовательностью последовательности  .●
.●
Над числовыми последовательностями будем выполнять арифметические действия по правилам:
a) 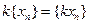 ; б)
; б)  +
+ 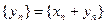 ; в)
; в) 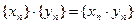 ;
;
г) 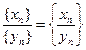 , если
, если 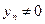 при всех
при всех 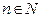 .
.
Задачи
1.1. Изобразить на координатной прямой числовые последовательности и найти среди них неограниченные последовательности:
a) 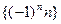 ; б)
; б) 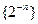 ; в)
; в) 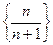 , г)
, г) 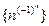 ; д)
; д) 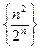 .
.
1.2. Доказать, что последовательность 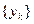 является подпоследовательностью последовательности
является подпоследовательностью последовательности  :
:
a) 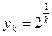 ,
, 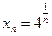 ; б)
; б) 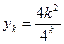 ,
, 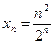 ; в)
; в) 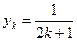 ,
, 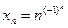
Дата добавления: 2016-06-05; просмотров: 1384;










