ЗАВИСИМОСТЬ РАБОТЫ И ВНУТРЕННЕГО КПД РЕАЛЬНОГО ЦИКЛА ОТ
π И Δ
А) – Зависимость работы и внутреннего КПД цикла от степени повышения давления π.
Качественно зависимость 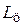 от
от 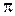 (при
(при 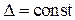 ) для реального цикла ГТД такова же, как и для идеального цикла Брайтона, изображенная на рис. 24.2. Но вместе с тем имеются и следующее отличие.
) для реального цикла ГТД такова же, как и для идеального цикла Брайтона, изображенная на рис. 24.2. Но вместе с тем имеются и следующее отличие.
Работа реального цикла равна 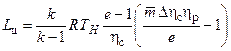 . Как видно, она также фавна нулю при p = 1 (потому, что тогда цикло просто нет) и при
. Как видно, она также фавна нулю при p = 1 (потому, что тогда цикло просто нет) и при 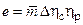 , т.е. при несколько меньше значении е (и, соответственно меньшем значении
, т.е. при несколько меньше значении е (и, соответственно меньшем значении 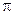 ), чем для идеального цикла. Дело в том, что в реальном цикле есть потери. И, хотя при
), чем для идеального цикла. Дело в том, что в реальном цикле есть потери. И, хотя при 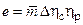 подвод теплоты к рабочему телу еще есть (т.к. при таком значении е ещё
подвод теплоты к рабочему телу еще есть (т.к. при таком значении е ещё 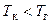 ), вся подведенная теплота расходуется только на преодоление гидравлических потерь, а на работу цикла уже ничего не остается.
), вся подведенная теплота расходуется только на преодоление гидравлических потерь, а на работу цикла уже ничего не остается.
Для определения оптимального (для работы цикла) значения p возьмем производную 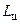 по е и приравняем её нулю. Тогда получим (опуская математику)
по е и приравняем её нулю. Тогда получим (опуская математику)
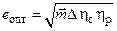 ,(24.9)
,(24.9)
т.е., как и для идеального цикла, 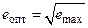 .
.
Рассмотрим далее зависимость внутреннего КПД реального цикла от p при D = const.
Как вы уже знаете, 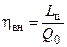 , где
, где 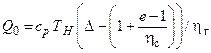 . Коэффициент
. Коэффициент 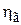 слабо зависит от p . Будем считать его постоянным. Поэтому, как следует из формулы для
слабо зависит от p . Будем считать его постоянным. Поэтому, как следует из формулы для 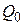 , приD = const значение
, приD = const значение 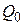 линейно уменьшается с ростоме .
линейно уменьшается с ростоме .
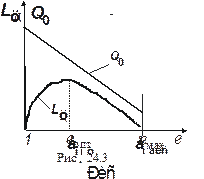
|
На рис. 24.3 изображена зависимость Lц и 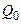 от е. Проанализируем эту зависимость.
от е. Проанализируем эту зависимость.
1). При е = еоптработа цикла максимальна. Поэтому при некотором увеличении е (и, соответственно, p)посравнению сеопт работа цикла еще почти не уменьшится. А 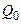 станет меньше, т.е.
станет меньше, т.е. 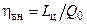 возрастет.
возрастет.
2). Но при приближении к еmaxработа цикла уменьшается вплоть до нуля при е =еmax, тогда как 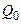 в реальном цикле, в отличие от идеального, как уже отмечалось, остается при е =еmax больше нуля. Поэтому при е =еmaxвнутренний КПД реального цикла ГТД обращается в нуль.
в реальном цикле, в отличие от идеального, как уже отмечалось, остается при е =еmax больше нуля. Поэтому при е =еmaxвнутренний КПД реального цикла ГТД обращается в нуль.
Из этого анализа следует, что:
а) – с ростом p внутренний КПД реального цикла не возрастает непрерывно, как у идеального цикла, а имеет максимум;
б) – этот максимум достигается при 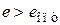 (т.е. при
(т.е. при 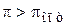 ).
).
Расчеты показывают, что это значение е (и p) оказывается значительно более высоким, чем соответствующее максимуму работы цикла.
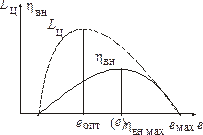 Рис.24.4
Рис.24.4
|
Так, например, при температуре перед турбиной порядка 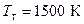 , что в стандартных атмосферных условиях (т.е. при
, что в стандартных атмосферных условиях (т.е. при 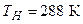 ) соответствует
) соответствует 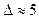 оптимальное значение p (обеспечивающее
оптимальное значение p (обеспечивающее 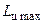 ) составляет
) составляет 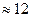 , а максимум
, а максимум 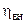 достигается при p
достигается при p 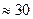 .
.
Таким образом, работа и внутренний КПД реального цикла зависят от π (при 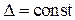 ) так, как показано на рис. 24.4.
) так, как показано на рис. 24.4.
В) – Зависимость работы и внутреннего КПД цикла от степени повышения температуры 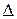 .
.
Из формулы работы реального цикла (24.6) следует, что (при π = const)
а) существуем минимальнаястепень подогрева 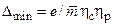 , при которой
, при которой 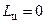 ; при меньшем значении D подводимой в процессе горения топлива теплоты недостаточно для покрытия гидравлических потерь;
; при меньшем значении D подводимой в процессе горения топлива теплоты недостаточно для покрытия гидравлических потерь;
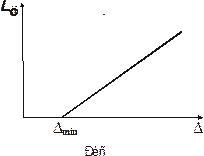 Рис. 24.5
Рис. 24.5
|
б) работа цикла зависит от степени подогрева линейно, следовательно, зависимость 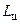 от Dимеет вил, изображенный на рис. 24.5.
от Dимеет вил, изображенный на рис. 24.5.
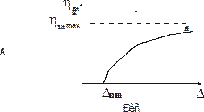 Рис. 24.6
Рис. 24.6
|
Далее; у идеального цикла Брайтона КПД не зависит от степени подогрева и равен 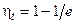 . Но у реального цикла при
. Но у реального цикла при 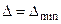 работа цикла равна нулю, а
работа цикла равна нулю, а 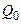 не равно нулю, и, следовательно,
не равно нулю, и, следовательно, 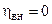 . А с увеличением степени подогрева (при данном значении π) и, соответственно, разности
. А с увеличением степени подогрева (при данном значении π) и, соответственно, разности 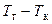 , все меньшая часть возрастающего
, все меньшая часть возрастающего 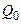 расходуется на покрытие гидравлических потерь. И поэтому внутренний КПД цикла возрастает, как показано на рис. 24.6, приближаясь в пределе к максимально возможному значению
расходуется на покрытие гидравлических потерь. И поэтому внутренний КПД цикла возрастает, как показано на рис. 24.6, приближаясь в пределе к максимально возможному значению 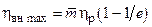 , которое следует из анализа формулы для
, которое следует из анализа формулы для 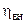 при
при 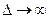 .
.
Работа цикла непосредственно связана с габаритами ГТД, так как при данном расходе воздуха (рабочего тела), а значит и при данном диаметре компрессора, получаемая в рабочем процессе энергия (которая затем тем или иным путем преобразуется в механическую работу, производимую двигателем) пропорциональна работе цикла. Поэтому прогресс в развитии авиационных ГТД идет в направлении увеличения максимально допустимой температуры газ перед турбиной (для увеличения D). Но одновременно надо увеличивать и значение p, так как с ростом D возрастают и 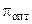 , и p, обеспечивающее достижение
, и p, обеспечивающее достижение 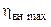 .
.
Повышение давления воздуха в процессе сжатия общем случае происходит во входном устройстве, а затем в компрессоре. Поэтому, пренебрегая малым различием между 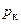 и
и 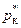 , можно записать, что π = πвхπк*, где
, можно записать, что π = πвхπк*, где
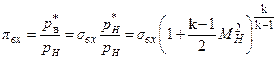 (24.10)
(24.10)
– степень повышения давления во входном устройстве,
При дозвуковых скоростях полета значения 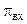 не превышают 1.2 …1.4, и поэтому для достижения необходимых значений p необходимо увеличивать значение
не превышают 1.2 …1.4, и поэтому для достижения необходимых значений p необходимо увеличивать значение 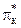 . И только на двигателях, предназначенных для самолетов, предназначенных для полета, в основном, на больших сверхзвуковых и гиперзвуковых скоростях полета, могут использовать компрессоры со сравнительно малыми значениями
. И только на двигателях, предназначенных для самолетов, предназначенных для полета, в основном, на больших сверхзвуковых и гиперзвуковых скоростях полета, могут использовать компрессоры со сравнительно малыми значениями 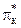 или вовсе бескомпрессорные двигатели (ПВРД или ГПВРД)
или вовсе бескомпрессорные двигатели (ПВРД или ГПВРД)
Дата добавления: 2018-05-10; просмотров: 1303;











