Кондуктивный теплообмен в цилиндрической стенке

Исходное уравнение в цилиндрической системе координат r, j, z имеет вид

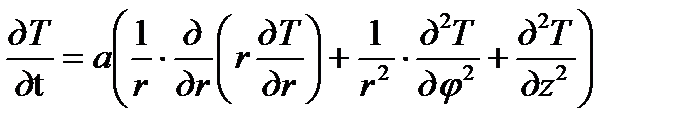. (11)

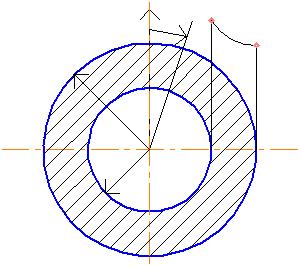
Считаем, что процесс теплообмена стационарный и длина цилиндра достаточно велика для того, чтобы пренебречь потоком тепла к его торцам вдоль оси z, процесс осесимметричный. При этих условиях температура является функцией только одной координаты – радиуса r (рис. 1.2):

;

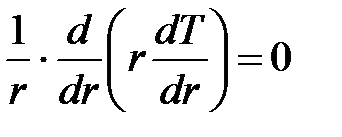или

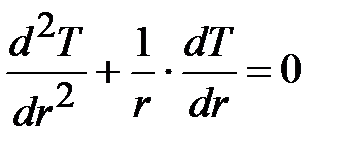. (12)

r

T1

j

T2

R1

R2

Рис. 1.2. Распределение температуры в цилиндрической стенке

Написав уравнение (12) в виде

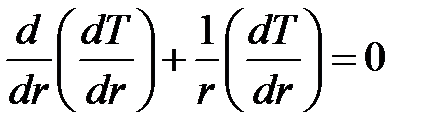
и разделив переменные, получим

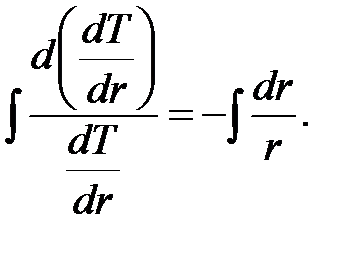
Выполняя интегрирование, находим

.

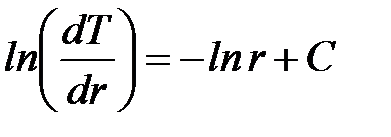Положив, что С = lnC₁, где C₁ – некоторая новая постоянная, получим

.

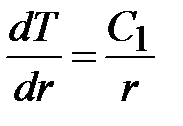Вторичное интегрирование дает

;

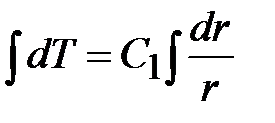T = C₁lnr + C₂. (13)

Постоянные интегрирования находим из граничных условий:

при ; ;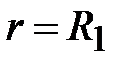

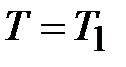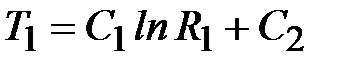при ; .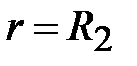

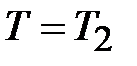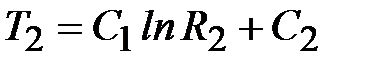Отсюда

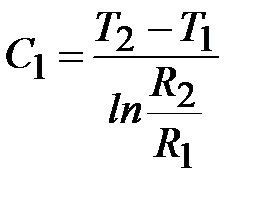; C₂ = T₁ - C₁ lnR₁.

Окончательно

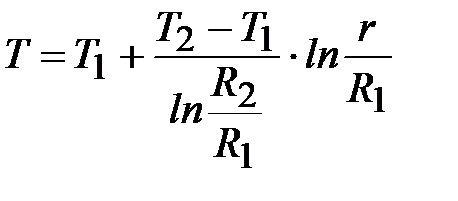. (14)

Как видно из уравнения (14) имеет место логарифмический закон распределения температуры по радиусу цилиндра.

Градиент температуры на внутренней поверхности цилиндра равен

.

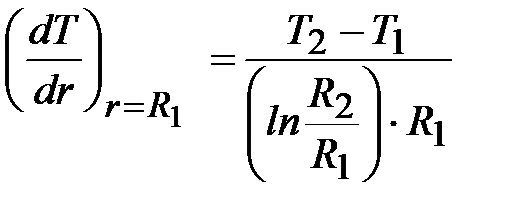В правой части уравнения для любого r в знаменателе вместо R₁ необходимо брать r.

Поток тепла за счет теплопроводности определяется как

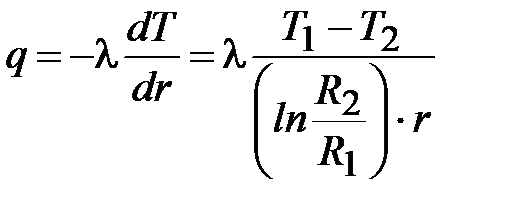. (15)

Как видно из уравнения (15) тепловой поток зависит от координаты r
и уменьшается с возрастанием r.

Количество теплоты находим как

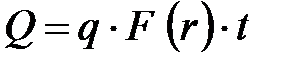. (16)

Здесь F = 2prL – внутренняя поверхность цилиндра, t – время, L – высота цилиндра.

Расход тепла определяется как

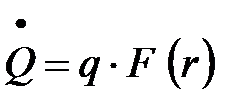. (17)

Если труба многослойная и состоит из n слоев, тогда для потока тепла получим

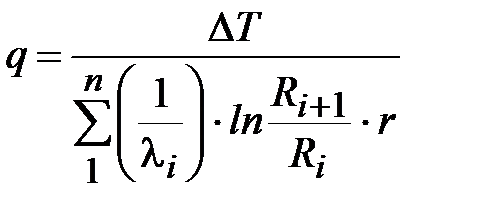. (18)

Здесь ∆T = T₁ – T_n – общая разница температуры.

Зависимость q_м и F от радиуса r не позволяет использовать традиционную форму уравнения теплопередачи для цилиндрической стенки. В этом случае используется коэффициент теплопередачи 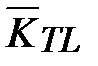отнесенный
к единице длины

, .

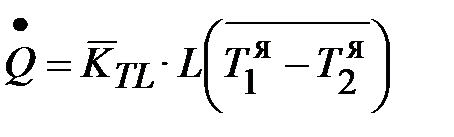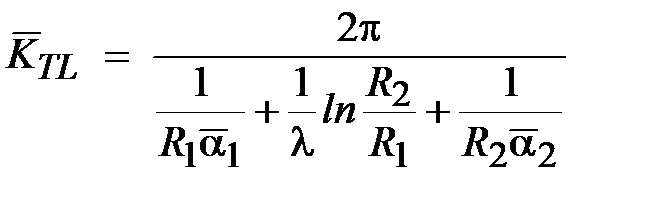Здесь 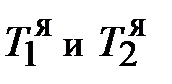– температуры в ядре фаз, омывающих цилиндрическую поверхность.

Для тонкостенных цилиндров, к которым можно отнести большинство труб, без большой ошибки можно использовать зависимости для плоской стенки.