Спектры некоторых периодических последовательностей

Спектральный состав периодической последовательности прямоугольных видеоимпульсов.

Рис. 1.6

,

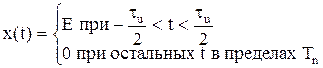где T_n – период повторения; Е – амплитуда импульса; t_u – длительность.

Отношение: Q = T_n/t_u – называется "скважностью".

Определим спектральный состав бесконечной последовательности видеоимпульсов. Находим постоянную составляющую:

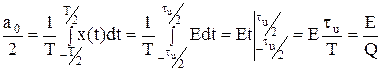
Так как функция x(t) в пределах t_u – четная, то необходимо искать гармонические составляющие – a_k (b_k = 0).

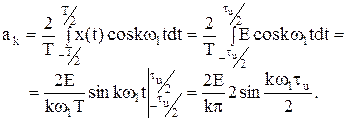
Тогда ряд Фурье будет:

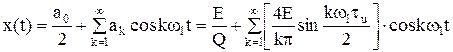. (1.6)

Исследуем полученное выражение. Здесь текущее, непрерывное значение имеет только сомножитель coskw₁t, тогда все остальные сомножители представляют численное выражение для спектральных составляющих, кратных w₁ = 2p/Т. Выражение в квадратных скобках – это число – численное значение гармонических составляющих, причем выражение 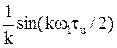- представляет собой по переменной
k – функцию sinc x = (sin x)/x и соответствует огибающей гармонического ряда, она обращается в нуль в точках частоты, которые можно найти из условия: 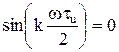что возможно, если wt_u/2 = p, откуда wt_u = 2p и
w = 2p/t_u тогда графическое отображение ряда Фурье будет (рис. 1.7):

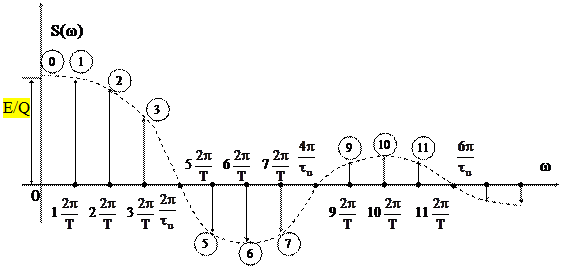Итак, спектральное разложение последовательности видеоимпульсов состоит из суммы дискретных гармонических составляющих, кратных 2p/Т, причем знак гармоник в разных "лепестках" графика отличается на 180°, что демонстрирует изменение их фазы на p и создает фазовый спектр.

С учетом разделения общего спектра на амплитудно-частотный и фазово-частотный графики спектрального разложения можно изобразить иначе (а также учтем, что w = 2pf и перейдем к герцовой частоте – f):

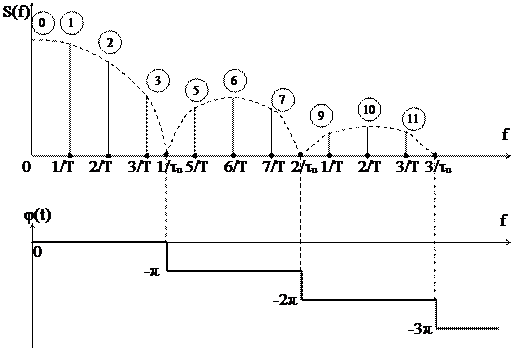а)

б)

Рис. 1.8

Обычно фазовочастотным спектром (рис. 1.8б) не интересуются (его упускают) и исследуют, в основном, амплитудно-частотный спектр, который жаргонно называют просто "спектр" (рис. 1.8а).

Рассмотрим влияние параметров последовательности видеоимпульсов на показатели амплитудного спектра.

А. Сначала изменим длительность импульса (t_u - var, Т = const). При увеличении длительности импульса (t_u2 = 2t_u1) спектр "сжимается" вдвое, при укорочении длительности (t_u3 = 0,5t_u1) спектр "расширяется" вдвое.

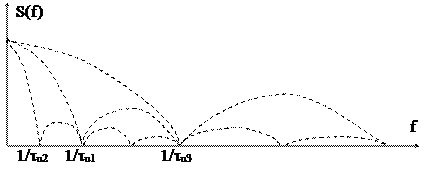А1. Если в пределе длительность импульса устремить к нулю t_u ® 0 (это принятый в математике единичный импульс, у которого длительность
t_u ® 0, а площадь остается равной единице S = 1, обозначают этот импульс d(t₀) – дельта-импульс), то спектральный состав первого лепестка спектра импульса расширяется до бесконечности, превращаясь в равномерный спектр от 0 до ¥ со спектральной плотностью G₀.

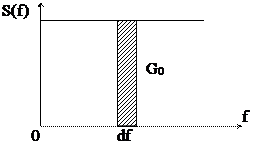А2. С другой стороны, при увеличении длительности импульса в пределе до бесконечности t_u ® ¥, получаем просто постоянный ток, спектральный состав которого выражается в одно единственное значение на частоте w = 0, т.е. значение постоянной составляющей.

Б. Теперь, не меняя длительности импульсов, будем изменять период повторения. t_u = const, Т – var.

Увеличим период вдвое, количество спектральных составляющих увеличится также вдвое, а расстояние по частоте сократится вдвое.

Рис. 1.11

Уменьшение периода повторения приводит к увеличению расстояния между дискретными гармониками. Уменьшим период повторения до величины Т = 2t_u, что приводит к колебанию типа "меандр" и построим для него спектр.

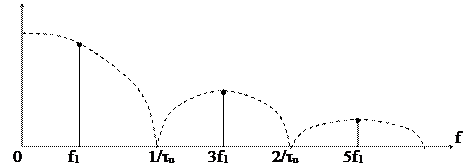Рис. 1.12

Получаем спектр, состоящий из нечетных гармоник (четные гармоники приходятся на нули огибающей спектра), т.е. получаем уже найденный выше спектр другим путем (см. рис. 1.4).

Б1. Теперь устремим период повторения видеоимпульсов в ¥, т.е. приходим к понятию единичного (одиночного) импульса. Спектральные составляющие постепенно сближаются и в пределе сливаются в сплошной спектр, который будет характеризоваться спектральной плотностью, т.е. энергией спектра, приходящейся на элемент текущего значения частоты df.

Спектральный состав одиночного импульса вырождается в функцию:

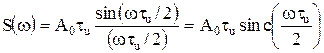. (1.7)

Рис. 1.13

При этом ряд Фурье переходит в интеграл, и получаем прямое и обратное преобразование Фурье:

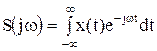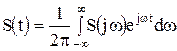; . (1.8)

В. Рассмотрим, теперь, ситуацию когда последовательность видеоимпульсов ограничена, т.е. сигнал выглядит в виде "пачки" импульсов с параметрами: количество импульсов – n, длительность одного импульса - t_u, период повторения – Т, D – длина "пачки" nT+t_u.

Рис. 1.14

Строим спектр "пачки" последовательно,

В1. сначала определим самый протяженный по частоте элемент спектра, он определяется самым коротким во времени элементом – самим импульсом с длительностью t_u.

В2. Затем примем, что последовательность импульсов бесконечна и в соответствии с предыдущим анализом бесконечной последовательности определим дискретные составляющие спектра, расположенные на расстояниях по частоте Df = 1/Т (рис. 1.16).

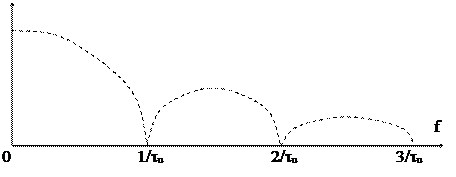Рис. 1.15

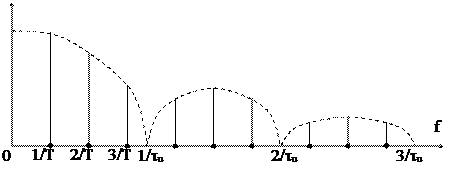
Рис. 1.16

В3. После этого рассмотрим спектр "пачки" импульсов, принимая длительность всей пачки за одиночный видеоимпульс, совмещая все приведенные рассуждения в единую систему, строим спектральную характеристику "пачки" видеоимпульсов.

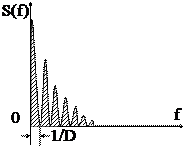Рис. 1.17 ­­– Спектр 1 импульса длиной D

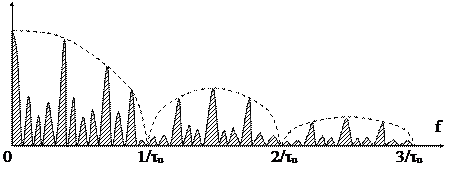Рис. 1.18 ­­– Спектр пачки импульсов

Г. И, наконец, рассмотрим спектральное разложение радиоимпульса, который отличается от видеоимпульса наличием заполнения несущим гармоническим колебанием частотой f₀ внутри импульса. Теперь видеоимпульс играет роль огибающей для радиоимпульса:

.

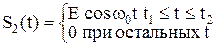Рис. 1.19

В соответствии с теоремой переноса спектра: S₂(w₀) = S₁(w₀ -w)

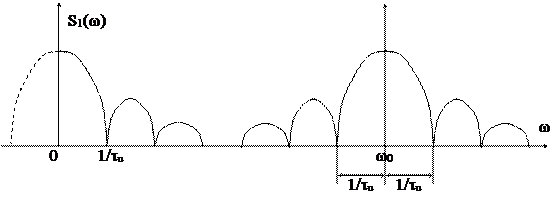Рис. 1.20

Имея в виду, что преобразование Фурье действует в пределах от
w = -¥ до w = +¥ (а мы исследуем только область положительных частот спектра, удваивая его энергию за счет несуществующей "отрицательной" полосы), спектр, перенесенный на несущее колебания с частотой - w₀ занимает область и справа и слева от значения несущей, как и следует из математически точного расчета спектра. Полоса занимаемых частот при этом удваивается.

Литература:

[1] стр. 42-48. [2] стр. 36-44. [3] стр. 36-45.

Контрольные вопросы:

1. Какая разница между амплитудным спектром и фазовым?

2. Какое отличие спектра периодического сигнала от непериодического?

3. Чем отличается спектр радиосигнала от спектра видеосигнала?

4. В чем особенности спектра ограниченной "пачки" сигналов?