Число степеней свободы (подвижность) механизмов

Поскольку механизм — кинематическая цепь, то при его иссле­довании возникает вопрос о числе степеней свободы, т. е. о числе ве­дущих звеньев, движением которых следует задаться, чтобы дви­жение остальных звеньев относительно стойки было вполне опре­деленным.

Известно, что если положение звеньев механизма определяется заданием W обобщенных (независимых) координат, то такой меха­низм обладает W степенями свободы. Следовательно, число обоб­щенных координат механизма W определяет число его ведущих звень­ев. Определим это число.

Если бы все п+1 звеньев пространственного механизма были подвижными и не связанными друг с другом кинематическими парами, их общее число степеней свободы было бы W = 6 (п + 1). Но все звенья составляют кинематическую цепь, пары которой накладывают на относительное движение звеньев определенное число связей (таблица 1.1). При наличии в пространственной цепи кинематических пар всех пяти классов,

₅

общее число связей будет т = Σ k p_k, а с учетом того, что на

^{k =1}

одно звено (стойку) наложено шесть связей, число степеней свободы механизма будет (формула Малышева):

₅

W = 6n-Σ kρ_k = 6n- 5p₅- 4p₄ - Зp₃ + 2p₂ - p₁, (1.1)

^{k =1}

где п - число подвижных звеньев механизма.

В плоских механизмах на каждое подвижное звено наложено три общих условия связи, не позволяющих реализовать степени свободы пар III, II и I классов, поэтому формула (1.1) принимает вид (фор­мула Чебышева):

W = 3n — 2n₅ —p₄. (1.2)

Все механизмы, удовлетворяющие условию (1.1), относятся к ну­левому семейству, а условию (1.2) - к третьему.

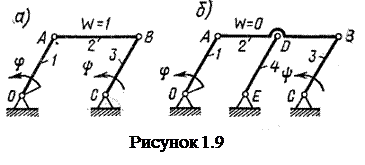
В машинах и приборах встречаются плоские механизмы, действи­тельное число степеней свободы которых не удовлетворяет условию (1.2). Это является следствием наличия лишних связей, введенных в механизм по различным причинам. В механизме шарнирного па­раллелограмма с одной степенью свободы (рисунок 1.9, б), например, такая связь появилась в результате шарнирного присоединения зве­на 4 к стойке О и шатуну 2 с целью повысить жесткость шатуна. «Лиш­нее» звено 4 и пары D и Е не изменили кинематики механизма, но отняли из расчетного числа W (формула 1.2) одну степень сво­боды. Связи, появляющиеся в механизмах в силу частных особенно­стей их структуры и не оказывающие влияния на кинематику механиз­ма, называются пассивными.

1.1.4 Образование плоских механизмов

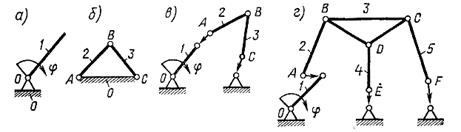
Из формулы (1.2) находим, что простейший механизм имеет два звена (рисунок 1.10, а), одно из которых (0) обращено в стойку, а второе (1), оставшееся подвижным, является и ведущим и ведомым. Обра­зование более сложных, многозвенных механизмов с W = 1, в кото­рых происходило бы преобразование движения ведущего звена t в движение ведомого звена п (в двухзвенном механизме такого пре­образования нет), осуществляется подвижным присоединением к двухзвенному механизму так называемых структурных групп (одной или нескольких). Последние представляют собой

		Рисунок 1.10

кинематические цепи (звенья 2 и 3), присоединение которых свободными элементами звень­ев к стойке 0 образует неподвижную (W = 0), статически определи­мую ферму ABC (рисунок 1.10, б), а присоединение к разным звеньям механизма (рисунок 1.10, б) не изменяет его подвижности.

Поскольку после присоединения к стойке группа теряет подвиж­ность, то число ее звеньев п' и число низших одноподвижных пар p'₅, считая и те, которые образовались в результате присоединения, долж­ны удовлетворять условию:

Зп'- 2p'₅ = 0. (1.3)

Таким образом, простейшая группа состоит из двух звеньев 2 и 3 (рисунок 1.10, в), соединенных в пару В, имеющих по одному свобод­ному элементу А и С. Такие группы называются двухповодковыми или диадами, а механизмы, в состав которых кроме ведущего звена и стойки входят диады, относят к второму классу и называют диадными. По данному условию могут быть образованы и более сложные группы: трехповодковые, например состоящие из звеньев 2...5 (рисунок 1.10, г), и др.

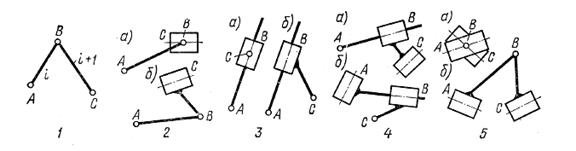
Ограничиваясь изучением диадных механизмов, получивших в тех­нике широкое распространение, рассмотрим их образование с по­мощью пяти разновидностей диад (рисунок 1.11, 1...5), полученных из диады первой модификации путем замены в ней одной или двух вра­щательных пар поступательными. (На практике наиболее часто при­меняются модификации 1, 2а, 3а, 5а.)

В процессе образования четырехзвенных механизмов

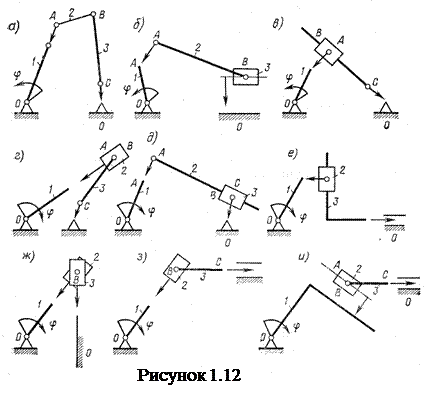
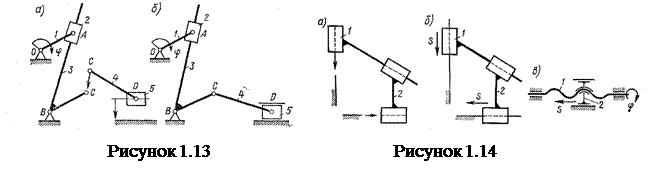
(рисунок 1.12, а...и) диады присоединяются свободными элементами звеньев А и С к ведущему звену 1 и стойке 0. Более сложные, многозвенные меха­низмы (рисунок 1.13, а, б) могут быть образованы аналогично, присо­единением последующих диад к любым двум звеньям ранее полученного четырехзвенного механизма.

	Рисунок 1.11

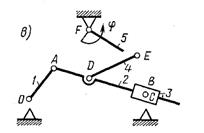
Обратим внимание на диаду, в которой все три пары являются поступательными (рисунок 1.14, а). Удовлетворяя условию (1.3) лишь формально, звенья этой группы после подвижного присоединения к стойке не теряют подвижности, а образуют плоский механизм с од­ной степенью свободы (рисунок 1.14, б). На звенья подобных механиз­мов наложено еще одно (четвертое) общее условие связи - их звенья лишены возможности вращаться вокруг осей, перпендикулярных плоскости движения, поэтому структурная формула таких механиз­мов имеет вид:

W = 2n-p₅. (1.4)

Плоские механизмы, на звенья которых наложено четыре общих связи и подчиняющиеся условию (1.4), составляют четвертое семей­ство. К ним относятся трехзвенные механизмы клинового типа (рисунок 1.14, б) и механизмы с винтовой парой (рисунок 1.14, в). В винто­вой паре независимым является только одно движение, поэтому ее относят к парам V класса (таблица 1.1, к).

Анализ механизмов

Поскольку любой по сложности плоский одноподвижный меха­низм с вращательными и поступательными парами образуется при­соединением к двухзвенному механизму одной или нескольких групп, то может быть произведено разложение любого одноподвижного пло­ского механизма на двухзвенный механизм и структурные группы. Разложение механизмов на группы (структурный анализ) значи­тельно упрощает решение задач силового анализа, облегчает выявление пассивных звеньев и позволяет определять класс механизма. Структурный анализ выполняется в такой последовательности. Определяется число степеней свободы. В механизме с одним ведущим звеном

(рисунок 1.10, а) это число равно единице. Если по формуле (1.2) получено W < 1, то в механизме имеются пассивные звенья - одно при W = 0 (рисунок 1.9, б), два при W = -1 и т. д. Перед анализом механизма эти звенья следует удалить. Сначала делается попытка отделить наиболее удаленную от ве­дущего звена диаду так, чтобы после этого остался механизм с тем же числом степеней свободы, что и заданный. Если диаду отделить не удается (число W оставшегося механизма не получается таким, как у заданного), то следует попытаться отделить трехповодковую или другую, более сложную группу. Разложение механизма с одной сте­пенью свободы на группы ведется до тех пор, пока не останется одна пара - ведущее звено со стойкой (рисунок 1.10, а).

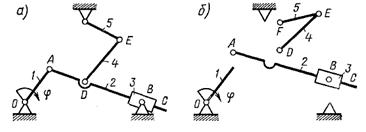
Согласно структурной классификации И. И. Артоболевского, класс механизма определяется наивысшим классом структурной группы. Однако следует иметь в виду, что с выбором другого ведущего звена, также входящего в пару V класса со стойкой, класс механизма может измениться. Если, например, в качестве ведущего звена меха­низма (рисунок 1.15, а) выбран кривошип 1, то от механизма могут быть отделены последовательно две диады: первой модификации (звенья 5 и 4) и третьей (звенья 2 и 3)

(рисунок 1.15, б). Если же за ведущее при­нять звено 5, то отделение диад окажется невозможным. В этом случае удается отделить только трехповодковую группу (звенья 1, 2, 3, 4, рисунок 1.15, в). Таким образом, в первом случае механизм будет отне­сен к диадным, т. е. ко второму классу, а во втором случае - к треть­ему.

	Рисунок 1.15