Метод двух реакций. Векторная диаграмма явнополюсного генератора без учета насыщения
В явнополюсной синхронной машине ротор в магнитном отношении является несимметричным (по продольной его оси воздушный зазор меньше, чем по поперечной). Это вызывает затруднения в учете влияния поля якоря на поле возбуждения.
Для облегчения учета реакции якоря в явнополюсной машине широко применяется метод двух реакций, предложенный в 1895 г. французским электротехником А. Блонделем.
Согласно этому методу 1-я гармоника МДС реакции якоря Fа раскладывается на две составляющие
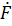 а =
а = 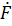 d +
d + 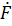 q.
q.
Составляющая 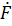 d совпадает с осью полюсов и является продольной составляющей реакции якоря. Составляющая Fq направлена перпендикулярно оси полюсов и является поперечной реакцией якоря. Можно принять, что первая составляющая создается током Id,а вторая — током Iq (см. рис. 2.7).
d совпадает с осью полюсов и является продольной составляющей реакции якоря. Составляющая Fq направлена перпендикулярно оси полюсов и является поперечной реакцией якоря. Можно принять, что первая составляющая создается током Id,а вторая — током Iq (см. рис. 2.7).
Можно считать, что в воздушном зазоре явнополюсного ненасыщенного синхронного генератора независимо существуют три магнитных потока: поток, созданный обмоткой возбуждения Фв, поток продольной реакции якоря Фad и поток поперечной реакции якоря Фaq. Каждый из потоков индуцирует в обмотке якоря ЭДС. Согласно второму закону Кирхгофа для обмотки якоря, подключённой к нагрузке, можно записать уравнение
Ė 0+ Ė ad + Ė aq = Ů + İ (ra+jxσ) (2.5)
В ненасыщенной машине ЭДС Ead, индуцируемая потоком Фad, будет пропорциональна продольному току Id:
Ead = xad Id (2.6)
Коэффициент пропорциональности xad называется индуктивным сопротивлением реакции якоря по продольной оси.
Для ЭДС Eaq можно записать аналогично:
Eaq = xaq Iq. (2.7)
Коэффициент пропорциональности xaq называется индуктивным сопротивлением реакции якоря по поперечной оси. В (2.5) через Е0 обозначена ЭДС, индуцируемая в обмотке якоря от потока возбуждения, созданного током Iв.
Индуцируемые в обмотке якоря ЭДС отстают по фазе от соответствующих потоков и создающих их токов на угол π/2. С учетом сказанного уравнения (2.6), (2.7) в комплексной форме будут иметь вид
Ė ad = -jxad İd ; Ė aq = -j xaq İq (2.8)
Подставив (2.8) в (2.5), получим
Ů = Ė 0 - jxad İd -j xaq İq - jxσİ - İ ra (2.9)
Рис. 2.10. Векторная диаграмма явнополюсного генератора без учета насыщения
По уравнению (2.9) на рис. 2.10 построена векторная диаграмма явнополюсного генератора, работающего на активно-индуктивную нагрузку. При построении предполагалось что были известны İ, Ė0,ψи параметры генератора. Требовалось определить напряжение генератора Ů. При построении диаграммы предварительно ток İ раскладывают на составляющие İd и İq а затем из Ė0вычитают векторы падений напряжения в той последовательности, как они записаны в (2.9).
Преобразуем уравнение (2.9). Для этого вектор падения напряжения в индуктивном сопротивлении рассеяния обмотки якоря выразим через составляющие тока İ;
- jxσİ = - jxσ.(İ d+ İ q). (2.10)
Подставляя (2.10) в (2.9), после преобразования получаем
Ů = Ė 0 – j(xad + xσ) İ d -j (xaq+xσ) İ q - İ ra .
Обозначим сумму индуктивных сопротивлений при токе İ d через xd :
xd = xad + xσ,
а сумму индуктивных сопротивлений при токе İ q через xq:
xq = xaq+xσ.
Индуктивное сопротивление xd носит название синхронного индуктивного сопротивления по продольной оси, а xq – синхронного индуктивного сопротивления по поперечной оси.
Дата добавления: 2017-11-21; просмотров: 2521;











