Использование специальных кодов при выполнении операций сложения и вычитания чисел в естественной форме

Понятие кодов в цифровых системах (ЦС).

В ЦС, с целью упрощения устройств, выполняющих арифметические операции, применяют специальные коды для представления чисел, в которых для изображения числа и его знака используются цифры двоичной системы счисления. К таким кодам относят прямой, обратный и дополнительный коды, которые называют ещё машинными кодами чисел.

Специальное кодирование чисел

Код числа в естественной форме, состоящей из кода знака и q - ичного кода его модуля, называется прямым кодом q-ичного числа. Разряд прямого кода числа, в котором располагается код знака, называется знаковым разрядом кода. Разряды прямого кода числа, в которых располагается q - ичный код модуля числа, называются цифровыми разрядами кода. При записи прямого кода q - ичного числа Х на бумаге знаковый разряд располагается левее старшего цифрового разряда и отделяется от цифровых разрядов точкой.

Известно, что при представлении чисел в прямом коде реализация операций сложения и вычитания в ЦС должна предусматривать различные действия с модулями чисел в зависимости от их знаков. Сложение в прямом коде с одинаковыми знаками выполняется достаточно просто. Числа складываются и сумме присваивается код знака слагаемых. Значительно более сложной является операция алгебраического сложения прямых кодов чисел с различными знаками. В этом случае приходится определять большее по модулю число, производить вычитание чисел и присваивать коду разности знак большего по модулю числа. Для упрощения выполнения операции алгебраического сложения чисел в ЦС, в частности в ЭВМ, используются специальные коды, позволяющие свести эту операцию к операции арифметического сложения специальных кодов. В качестве специальных в ЭВМ применяются обратный и дополнительный коды. Для представления чисел в специальном коде используется дополнительный разряд с определенным весом. В качестве дополнительного обычно используется знаковый разряд прямого кода.

Правило 1.Специальный код положительного числа совпадает с его прямым кодом и, наоборот, прямой код положительного числа совпадает с его специальным кодом.

Обратный код числа

Специальный код числа, в котором кроме (n+r) цифровых разрядов с весами от q^n-1до q^-r используется дополнительный разряд с весом (-qⁿ+q^-r) называется обратным q-ичным кодом числа. Для обозначения обратного q-ичного кода числа X_q будем использовать запись вида [X_q]_ОК.

Для двоичного числа можно сказать, что обратный код, это специальный код, инвертированный во всех разрядах, кроме знакового

Правило 2. Для преобразования q-ичного кода или прямого q-ичного кода отрицательного числа в обратный код или наоборот для преобразования обратного кода отрицательного числа в прямой код необходимо в дополнительный (знаковый) разряд записать цифру 1, а в цифровые разряды записать коэффициенты x_i, определяемые из соотношения:

x_i=(q-1)-x_i , -r £ i £ n-1, (1.26)

где: q - основание системы счисления;

x_i - цифра в i-ом разряде исходного кода числа X.

Пример 1.21. Образовать обратные коды чисел:

1) X₁₀= 95,28; X₁₆= A5,1C; X₈= 63,27; X₂= 101,011;

2) X₁₀=-85,38; X₁₆=-AB,CD; X₈=-57,46; X₂=-101,11.

Решение. 1. Поскольку числа положительные, то в соответствии с правилом 1 их обратные коды равны прямым кодам: [X₁₀]_ок = 0.95.28; [X₁₆]_ок = 0.A5.1C; [X₈]_ок = 0.63.27; [X₂]_ок=0.101.011.

2. Так как числа отрицательные, то в соответствии с правилом 2 их обратные коды равны:

[X₁₀]_ок = 1.14.61; [X₁₆]_ок = 1.54.32; [X₈]_ок = 1.20.31; [X₂]_ок = 1.010.00.

Пример 1.22. Образовать прямые и q-ичные коды чисел, если их обратные коды равны:

1) [X₁₀]_ок= 0.18.75; [X₁₆]_ок= 0.E8.94; [X₈]_ок= 0.54.36; [X₂]_ок= 0.110.01;

2) [X₁₀]_ок= 1.75.26; [X₁₆]_ок= 1.54.A5; [X₈]_ок= 1.37.25; [X₂]_ок= 1.001.10.

Решение. 1. Так как исходные коды положительные, то в соответствии с правилом 1:

[X₁₀]_пк=0.18.75; X₁₀=18,75; [X₁₆]_пк=0.E8.94; X₁₆=E8,94; [X₈]_пк=0.54.36; X₈=54,36; [X₂]_пк=0.110.01 X₂=110,01.

2. Поскольку исходные коды отрицательные, то в соответствии с правилом 2 [X₁₀]_пк=1.24.73; X₁₀=-24,73; [X₁₆]_пк=1.AB.5A; X₁₆=-AB,5A; [X₈]_пк =1.40.52; X₈=-40,52; [X₂]_пк=1.110.01; X₂=-110,01. Поскольку для двоичной СС (q-1)=1, то из правила 2 следует частное правило преобразования кодов двоичных чисел в обратные коды и наоборот.

Правило 3. Для преобразования двоичного кода или прямого кода двоичного отрицательного числа в обратный код и наоборот для преобразования обратного кода отрицательного числа в прямой код, необходимо в дополнительный (знаковый) разряд записать цифру 1 и во всех цифровых разрядах заменить нули на единицы, а единицы на нули.

Таким, образом, из правила 3 следует, что для образования обратного кода отрицательного двоичного числа необходимо заменить значения цифровых разрядов на обратные. Это и обусловило название этого специального кода.

Дополнительный код

Служит для унификации операций сложения и вычитания.

Специальный код числа, в котором кроме (n+r) цифровых разрядов с весами от q^n-1 до q^-r используется дополнительный разряд с весом (-qⁿ ) называется дополнительным кодом q-ичного числа. Для обозначения дополнительного кода числа X_q будем использовать запись вида [X_q]_дк.

Другими словами, дополнительный код, это дополнение кода отрицательного числа до основания q (Например, для двоичного числа дополнение до основания 2. В результате каждый разряд отрицательного числа инвертируем, а к последнему разряду добавляем 1).

Правило 4. Для преобразования q-ичного кода или прямого q-ичного кода отрицательного числа в дополнительный код или наоборот для преобразования дополнительного кода отрицательного числа в прямой код необходимо в дополнительный (знаковый) разряд записать цифру 1, а в цифровые разряды записать коэффициенты x_i, определяемые из соотношений:

x_i=(q-1)-x_i, если (-r+1) £ i £ n-1; x_i= q-x_i, если i =-r,

где q - основание системы счисления; x_i - цифра в i-ом разряде исходного кода числа X.

Из определения дополнительного кода и правила 4 видно, что дополнительный код отрицательного числа отличается от обратного на единицу младшего разряда.

Пример 1.23. Образовать дополнительные коды чисел:

1) X₁₀= 18,29; X₁₆=A4,15; X₈=46,13; X₂=101,011;

2) X₁₀=-18,29; X₁₆= -44,15; X₈=-46,13; X₂=-101,011.

Решение. 1. Поскольку числа положительные, то в соответствии с правилом 1 их дополнительные коды равны прямым кодам:

[X₁₀]_дк=0.18.29; [X₁₆]_дк=0.A4.15; [X₈]_дк=0.46.13; [X₂]_дк=0.101.011.

2. Так как числа отрицательные, то в соответствии с правилом 4 их дополнительные коды равны:

[X₁₀]_дк= 1.81.71; [X₁₆]_дк= 1.58.EB; [X₈]_дк= 1.31.65; [X₂]_дк= 1.010.101.

Пример 1.24. Образовать прямые и q-ичные коды чисел, если:

1) [X₁₀]_дк= 0.58.69; [X₁₆]_дк= 0.A1.B9; [X₈]_дк= 0.34.56; [X₂]_дк= 0.100.11;

2) [X₁₀]_дк= 1.58.69; [X₁₆]_дк= 1.A1.B9; [X₈]_дк= 1.34.56; [X₂]_дк= 1.100.11.

Решение. 1. Так как исходные коды положительные, то в соответствии с правилом 1: [X₁₀]_пк=0.58.69; X₁₀=58,69; [X₁₆]_пк=0.A1.B9; X₁₆=A1,B9; [X₈]_пк=0.34.56; X₈=34,56; [X₂]_пк=0.100.11; X₂=100,11.

2. Поскольку исходные коды отрицательные, то в соответствии с правилом 4: [X₁₀]_пк=1.41.31; X₁₀=-41,31; [X₁₆]_пк= 1.5E.47; X₁₆=-5E,47; [X₈]_пк=1.43.22; X₈=-43,22; [X₂]_пк=1.011.01; X₂=-11,01.

Пример 1.25. Образовать прямые и q-ичные коды чисел, если: [X₁₀]_дк= 1.54.08; [X₁₆]_дк=1.5A.B2; [X₈]_дк= 1.56.25; [X₂]_дк= 1.011.01.

Решение. Поскольку исходные коды отрицательны, то в соответствии с правилом 4: [X₁₀]=1.45.9 и X₁₀=-45,92; [X₁₆]_пк=1.A5.4E и X₁₆=-A5,4E; [X₈]_пк=1.21.53 и X₈ =-21,53; [X₂]_пк=1.100.11 и X₂=-100,11.

В общем случае дополнительный код отрицательного числа есть его дополнение до числа X_q=qⁿ, этим и обусловлено его название.

Заметим, что специальные коды не изменяют значения числа.

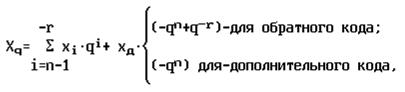(1.28)

Значение числа X_q можно определить по его специальному коду, если воспользоваться выражением (1.28), где x_д- значение дополнительного разряда специального кода; x_i- значение i-го цифрового разряда специального кода.

Пример 1.26. Определить X₁₀, если [X₁₀]_ок=1.81.70; [X₁₀]_дк= 1.81.71.

Решение. Пользуясь выражением (1.28) и учитывая, что для данного примера n = r = 2, получим:

-для обратного кода X₁₀=(-10²+10^-2)*1+8*10¹+1*10⁰+7*10^-1+0*10^-2=-18,29;

-для дополнительного кода X₁₀=-10²+8*10¹+1*10⁰+7*10^-1+1*10^-2=-18,29.

Таким образом, дополнительный код двоичного числа образуется из прямого кода инверсией и добавлением единицы к младшему разряду. Если результат получился отрицательным, то чтобы получить прямой код необходимо осуществить инверсию, а затем добавить единицу к младшему разряду. Единица переполнения знакового разряда при использовании дополнительного кода отбрасывается.

Использование специальных кодов при выполнении операций сложения и вычитания чисел в естественной форме

Специальные коды используются для осуществления операций сложения и вычитания.

Однако, при осуществлении указанных операций происходит переполнение разрядной сетки, в результате чего получаем ошибку. Для устранения данного недостатка используют модифицированный специальные коды.