Математический маятник

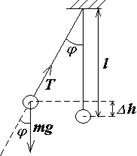Математическим маятником называется колебательная система состоящая из массивного точечного тела подвешенного в поле сил тяжести на нерастяжимой невесомой нити.

В нижней точке маятник обладает минимумом потенциальной энергии. Отклоним маятник на угол j . Центр тяжести массивного точечного тела поднимется на высоту Dh и при этом потенциальная энергия маятника возрастет на величину mgDh. Кроме того в отклоненном положении на груз действует сила тяжести и сила натяжения нити. Линии действия этих сил не совпадают, и на груз действует результирующая сила стремящаяся вернуть его в положение равновесия. Если груз не удерживать, то под действием этой силы он начнет перемещаться в исходное равновесное положение, его кинетическая энергия вследствие возрастания скорости будет увеличиваться, при этом потенциальная энергия будет уменьшаться. При достижении точки равновесия на тело уже не будет действовать результирующая сила (сила тяжести в этой точке компенсируется силой натяжения нити). Потенциальная энергия тела в этой точке будет минимальна, а кинетическая энергия напротив, будет иметь свое максимальное значение. Тело, двигаясь по инерции, пройдет положение равновесия и начнет от него удаляться, что приведет к возникновению результирующей силы (от силы натяжения и силы тяжести), которая будет направлена против движения тела, тормозя его. При этом начинается уменьшение кинетической энергии груза и возрастания его потенциальной энергии. Этот процесс будет продолжаться до полного исчерпания запасов кинетической энергии и перехода ее в потенциальную. При этом отклонение груза от положения равновесия достигнет максимальной величины и процесс повторится. Если в системе нет трения, колебания груза будут происходить бесконечно долгое время.

Таким образом, колебательные механические системы характеризуются тем, что при отклонении их из положения равновесия в системе возникает возвращающая сила стремящаяся вернуть систему в положение равновесия. При этом возникают колебания сопровождающиеся периодическим переходом потенциальной энергии системы в ее кинетическую энергию и обратно.

Рассчитаем колебательный процесс. Момент сил М действующий на маятник очевидно равен -mglsinj Знак минус отражает тот факт, что момент сил стремится вернуть груз в положение равновесия. С другой стороны по основному закону вращательного движения М=Id²j /dt² . Таким образом, получим равенство

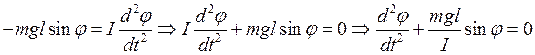
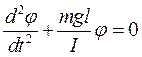Будем рассматривать только малые углы отклонения маятника из положения равновесия. Тогда sinj ≈j. И наше равенство примет вид:

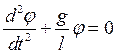Для математического маятника справедливо I= ml² . Подставляя это равенство в полученное выражение, получаем уравнение описывающее процесс колебания математического маятника:

Это дифференциальное уравнение описывает колебательный процесс. Решением этого уравнения являются гармонические функции sin(wt+j₀) или cos (wt+j₀) Действительно подставим любую из этих функций в уравнение и получим: w²=g/l. Таким образом, если это условие выполнено, то функции sin(wt+j₀) или cos(wt+j₀) превращают дифференциальное уравнение колебаний в тождество.

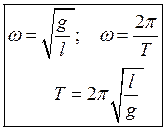Отсюда циклическая частота и период колебаний гармонического маятника выражается как:

Амплитуда колебаний находится из начальных условий задачи.

Как видим, частота и период колебаний математического маятника не зависит от массы груза и зависят только от ускорения свободного падения и длины нити подвеса, что позволяет использовать маятник как простой, но очень точный прибор для определения ускорения свободного падения.