ОДНОРОДНАЯ СИСТЕМА ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
ИЗ m УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ
Пусть дана однородная СЛАУ, состоящая из m линейных уравнений с n неизвестными
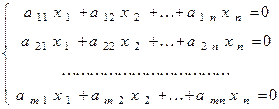 . (1)
. (1)
Отметим, что добавление столбца из нулей не изменяет ранга матрицы СЛАУ (1). Поэтому на основании теоремы Кронекера-Капелли эта система всегда совместна и имеет, по крайней мере, нулевое решение (x1 =x2 = ...,= xn=0). Если определитель системы (1) отличен от нуля и число уравнений равно числу неизвестных, то по теореме Крамера, нулевое решение является единственным.
Рассмотрим теперь другой случай, когда ранг матрицы СЛАУ (1) меньше числа неизвестных, то есть r(A)<n. Тогда данная система кроме нулевого решения может иметь и ненулевые решения. Для нахождения этих решений нужно в системе (1) выделить r линейно независимых уравнений, а остальные отбросить. В выделенных уравнениях в левой части оставляем r базисных неизвестных, а остальные n-r свободных неизвестных переносим в правую часть. В результате, приходим к системе
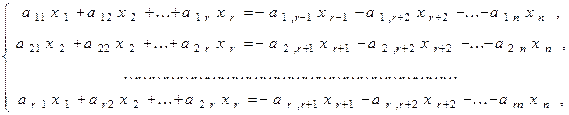 (2)
(2)
решение которой можно определить по формулам Крамера или Гаусса.
В данной системе имеем r базисных неизвестных x1, x2,..., xr и n-r - свободных неизвестных: xr+1, xr+2 , ..., xn . Система (2) имеет бесчисленное множество решений. Однако, среди этого множества есть решения линейно независимые между собой.
ОПРЕДЕЛЕНИЕ. Фундаментальной системой решения СЛАУ называются n-r линейно независимых решений однородной системы уравнений.
ПРИМЕР. Дана однородная система уравнений
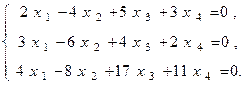
Найти ее общее решение и фундаментальную систему уравнений.
 Ш а г 1. Вычислим ранг матрицы системы, используя элементарные преобразования:
Ш а г 1. Вычислим ранг матрицы системы, используя элементарные преобразования:
а) отбрасываем 2-й столбец, так как он пропорционален 1-му;
б) 3-й столбец сначала умножим на (-2) и прибавим ко 2-му, а затем умножим его на (-3) и сложим с 1-м, умножим на 2;
в) отбрасываем 1-й столбец, так как он пропорционален 2-му;
г) 1-й столбец умножим на 3 и прибавим ко 2-му;
д) 1-ю строку умножим на 5 и прибавим к 4-й;
е) отбрасываем 3-ю строку и делим 1-ю на (-1), а 2-ю - на 2.
Имеем
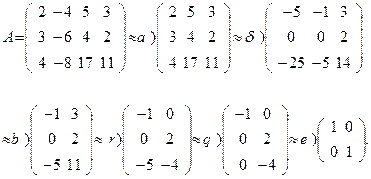
Так как r(A)=2, то есть r £ min(m,n), то данная система имеет фундаментальную систему решений, число которых n-2=4-2=2.
Определим теперь общее решение системы. Для этого определим базисный минор, то есть минор второго порядка, отличный от нуля. Таким минором является, например, минор, составленный из коэффициентов при x3 и x4 в первом и втором уравнениях системы: 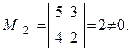 Оставляя базисные неизвестные x3 и x2 в левой части и перенося свободные неизвестные x1 и x2 в правую часть, приходим к системе
Оставляя базисные неизвестные x3 и x2 в левой части и перенося свободные неизвестные x1 и x2 в правую часть, приходим к системе
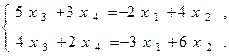
Ее решение, которое определим по формулам Крамера, имеет вид:
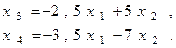
Чтобы получить фундаментальную систему решений нужно найти любые два линейно независимых решения данной системы. Полагая сначала x1 = 1, x2 =0, имеем x3 =-2,5; x4 =3,5; полагая затем x1 =0, x2 =1, получим x3 =5, x4 =-7.
Таким образом, фундаментальная система решений имеет вид
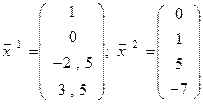 ,
,
а общее решение 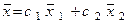 , где с1 и с2 - произвольные числа.
, где с1 и с2 - произвольные числа.
Дата добавления: 2016-06-05; просмотров: 2177;











