Гармонические колебания. Математические способы представления синусоидальных гармонических колебаний.

Колебательный процесс называется гармоническим или синусоидальными, если мгновенные значения эдс, напряжения или тока изменяется во времени по закону:

e(t)= Em sin(ωt + ψ ) или e=Em cos( ωt + ψ ′ )

u(t) =Um sin(ωt + ψ ) или u =Um cos( ωt + ψ ′ )

i(t) =Im sin(ωt + ψ ) или i =Im cos( ωt + ψ ′ ),

где e(t), u(t), i(t)- мгновенные значения величин (т.е. значения в данный момент времени, обознаются строчными буквами, иногда, просто e,u,i).

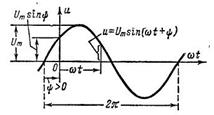
Амплитуды Em, Um, Im - максимальные значения величин. Период Т = 1/f, где f − частота колебания. Величина θ =ωt +ψ называется текущей фазой колебания и представляет собой некоторый угол, величина которого зависит от времени. Постоянная величина ψ (ψ′) называется начальной фазой, определяющей величину смещения гармонической функции относительно начала координат.

Величина ω пропорциональна частоте f; она носит название угловой частоты и равна ω =2 π f = 2 π / T. Угловая частота является скоростью изменения текущей фазы, т. е. ω = dθ/dt, и измеряется в радианах в секунду (рад/сек). При t=0 значение функции определяется величиной начальной фазы u (0)=Umcos ψ .

Большая часть электрической энергии вырабатывается в виде эдс, изменяющейся во времени также по закону синусоидальной функции. Источником такой эдс может быть синхронный генератор: металлическая рамка, вращающаяся в равномерно распределенном постоянном магнитном поле с угловой частотой ω. Токи и напряжения элементов линейной электрической цепи, присоединенной к такому генератору, изменяются во времени в виде функции синуса, повторяя форму эдс.

В цепи гармонического синусоидального тока во всех ветвях угловая частота ω известна. Неизвестны и подлежат определению амплитуды и фазы. Амплитуда и фаза– это символы, характеризующие гармоническую (синусоидальную) функцию. Синусоидальную функцию можно изобразить вектором. Если вектор Аm вращается против часовой стрелки с частотой ω, то, расположив точки, соответствующие его проекциям в фиксированные моменты времени на оси времени, получаем синусоиду, и наоборот, функцию синуса можно представить таким вращающимся вектором.

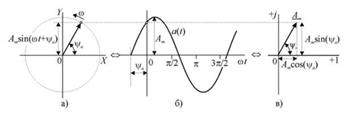
Любой вектор можно задать в декартовой (координатами конца вектор) или полярной системе координат (длина вектора и угол наклона – его оси). Оба эти способа можно объединить на комплексной плоскости, представив вектор в виде комплексного числа.

Комплексное число: a+ib, где a,b - действительные числа, i (j) - формальный символ, для которого справедливы равенства: i = (-1)^1/2; i ²=-1.

В таблице приведены основные математические действия с комплексными числами и изображение вектора на комплексной плоскости:

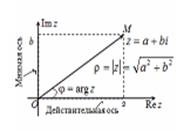|z| - модуль, φ – аргумент комплексного числа.

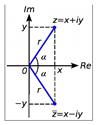
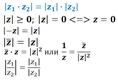
Формулы Эйлера: e^ix= cosx+isinx; cosx = (e^ix +e^-^ix)/2; sinx= (e^ix -e^-^ix)/2

Комплексное число представляют четырьмя способами:

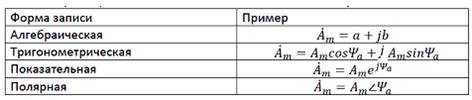
Первые три формы используются для вычислений: складывать и вычитать удобно в алгебраической форме, умножать и делить – в показательной. Укорочено комплексное число записывают, используя символ подчеркивания, или ставят точку сверху 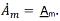. Подчеркивание сверху означает сопряженное число.

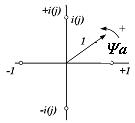
eⁱ^Ψ^a= cosΨa + isinΨa= a+ib, a= cosΨa, b=sinΨa Модуль |eⁱ^Ψ^a|=(cos²Ψa + sin²Ψa)^1/2=1, аргумент: argΨa= arctg(tgb/a)=arctg(sinΨa/ sinΨa)= Ψa . Функция eⁱ^Ψ^a – оператор поворота, т.к. при изменении Ψa изображающий ее вектор поворачивается на комплексной плоскости. Ψa=0, eⁱ⁰= cos0 + isin0=1; Ψa=π, eⁱ¹⁸⁰= cos180 + isin180=-1 Ψa=π/2, eⁱ⁹⁰= cos90 + isin90=i Ψa=-π/2, e-ⁱ⁹⁰= cos(-90) + isin(-90)=- i

Выражение гармонической функции через ее комплексную амплитуду и оператор поворота называется символическим представлением.

i(t) =Imsin(ωt + ψ ),

Текущая фаза Φ(t)=ωt +ψ. I_m(t)= I_meⁱ^Φ⁽^t⁾ Оператор поворота: eⁱ^Φ⁽^t⁾=cos Φ(t)+isin Φ(t).

I_m(t)= Im eⁱ ^Φ⁽^t⁾= I_mcos Φ(t) + iI_msin Φ(t) – комплексная функция времени для тока.

Мгновенное значение гармонического тока равно мнимой части этой комплексной функции времени: i(t)= I_msin Φ(t)=Imaginary I_m(t),Определив комплексную функцию времени всегда можно найти мгновенное значение гармонической функции.

I_m(t)= Im eⁱ ^Φ⁽^t⁾=Im eⁱ^(ω^t^{+ ψ)}= Imeⁱ^ψ eⁱ^ω^t=I_m eⁱ^ω^t, где I_m = Imeⁱ^ψ – комплексная амплитуда гармонической функции тока, | I_m | = | Imeⁱ^ψ | = Im модуль комплексной амплитуды, eⁱ^ω^t– оператор поворота.

В момент времени t=0, I_m(t)= Imeⁱ^ψ =I_mcos ψ + iI_msin ψ В момент времени t= t₁, I_m(t)= Imeⁱ^(ω^t^{1 +}^ψ)= Imeⁱ^ψeⁱ^ω^t¹ Вектор повернется на угол ωt1.

Дата добавления: 2017-11-21; просмотров: 1633;