Схема замещения трансформатора

Уравнениям (2.8) и (2.9) соответствует электромагнитная схема замещения (рис. 2.6).

Для выполнения аналитических расчетов трансформатора магнитную связь между обмотками удобно заменить электрической. С этой целью вторичную обмотку трансформатора необходимо привести к первичной по числу витков. Формально приведение осуществляется путем умножения второго уравнения системы (2.8) на коэффициент трансформации :

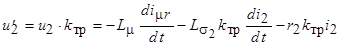, (2.10)

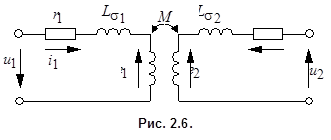
где 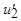- приведенное значение напряжения вторичной обмотки.

Из условия равенства мощностей приведенной и неприведенной обмоток

получаем выражение для приведенного тока:

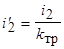. (2.11)

С учетом этого выражения уравнение (2.10) приобретает вид

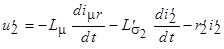, (2.12)

где ; .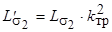

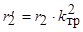Реактивная составляющая намагничивающего тока 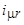приведенного трансформатора определяется суммой токов,

.

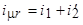Если теперь уравнения приведенного трансформатора записать в виде

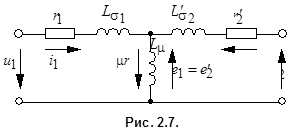
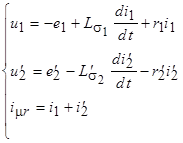(2.13)

и учесть, что 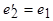, то электромагнитную связь в схеме (рис. 2.6) можно заменить электрической (рис. 2.7).

Схема замещения трансформатора (рис. 2.7) является его расчетной схемой при анализе как установившихся, так и переходных процессов.

При синусоидальных напряжениях и токах для описания установившихся режимов вместо дифференциальных уравнений удобнее пользоваться комплексными уравнениями для действующих значений токов и напряжений. Чтобы получить комплексные уравнения трансформатора, нужно заменить 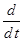на :

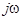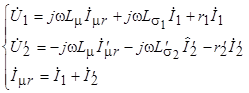(2.14)

Введем обозначения:

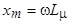- индуктивное сопротивление взаимной индукции;

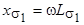- индуктивное сопротивление рассеяния первичной обмотки;

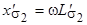- индуктивное сопротивление рассеяния вторичной обмотки;

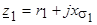- комплексное сопротивление первичной обмотки;

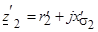- комплексное сопротивление вторичной обмотки.

Уравнения в новых обозначениях имеют вид

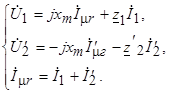(2.15)

При выводе уравнений трансформатора предполагалось, что процесс намагничивания сердечника не связан с потерями энергии на гистерезис и вихревые токи. Их можно учесть приближенно, приняв допущение, что потери в стали пропорциональны следующим величинам:

,

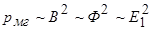отсюда ясно, что потери в стали можно учесть, если параллельно сопротивлению 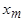включить активное сопротивление 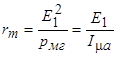(рис. 2.8, а). При расчетах удобно параллельные ветви свернуть в одну ветвь (рис. 2.8, б) с активным сопротивлением:

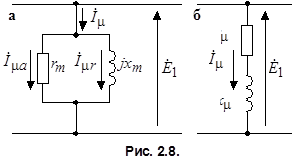
и индуктивным сопротивлением

.

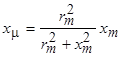Тогда уравнения трансформатора с учетом потерь в стали примут вид

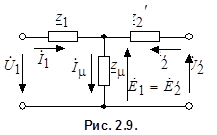
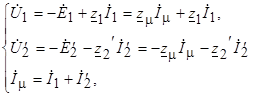, (2.16)

где .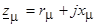

Уравнениям (2.16) соответствует Т-образная схема замещения приведенного трансформатора, представленная на рис. 2.9.

Численные расчеты по уравнениям (2.16) и соответствующей им схеме замещения (рис. 2.9) обычно выполняют в относительных единицах. В качестве базисных принимаются

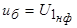- действующее значение номинального фазного напряжения первичной обмотки;

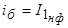- действующее значение номинального фазного тока первичной обмотки;

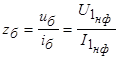- фазное сопротивление номинальной нагрузки.

Переход к относительным единицам осуществляется путем деления величин в именованных единицах на соответствующие базисные значения.

Сопротивления трансформатора в относительных единицах имеют следующий порядок:

; ;

;

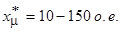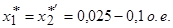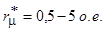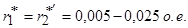
Необходимо отметить, что сопротивления 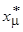и 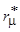не являются постоянными. Они зависят от насыщения магнитопровода. Остальные сопротивления можно считать практически постоянными для всех режимов работы трансформатора.