Метод зон Френеля. Зонные пластинки

<9 10 111213 14 15 >

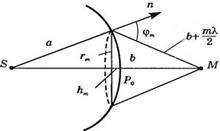
Построение зон Френеля: Согласно принципу Гюйгенса – Френеля, действие источника S заменяют действием воображаемых источников, расположенных на волновой поверхности Ф. Амплитуда световой волны находится в точке М.

Френель волновую поверхность Ф разбил на кольцевые зоны такого размера, чтобы расстояния от краев зоны до точки М отличалась на :

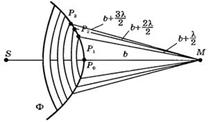
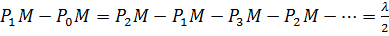
Колебания от соседних зон проходят до точки M расстояния, отличающиеся на половину длины волны, поэтому в точку М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять

Рис. 3.1.2 друг друга. Тогда амплитуда результирующего светового колебания в точке М: 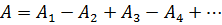, где А1, А2, А3 и т.д.- амплитуды колебаний, возбуждаемых 1-й, 2-й,… зонами.

Внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высотой 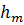. Учитываем, что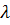 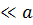и .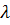

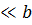Площадь сферического сегмента:

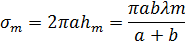
Площадь m-й зоны Френеля:

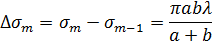
Радиус внешней границы m-й зоны Френеля: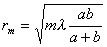

С ростом m уменьшается интенсивность излучения в направлении М:

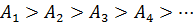
Общее число зон, уменьшающихся на полусфере, огромно, а их площади очень малы, поэтому: 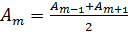и тогда амплитуда

Рис. 3.1.3. результирующих колебаний в точке М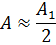

Таким образом, распространение света от S к M происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SM, т.е. прямолинейно.

Зонные пластинки – в простейшем случае стеклянные пластинки, на поверхность которых нанесены по принципу расположения зон Френеля чередующиеся прозрачные и непрозрачные кольца радиусами, определяемыми для заданных значений a,b, 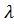выражением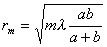

Рис. 3.1.4 Если поместить зонную пластинку в строго определенном месте (на расстоянии a от точечного источника и на расстоянии b от точки наблюдения на линии, соединяющей эти две точки), то она для света длиной волны 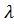перекроет четные зоны и оставит свободными нечетные, начиная с центральной. В результате результирующая амплитуда 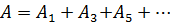должна быть больше, чем при полностью открытом волновом фронте. Опыт подтверждает эти выводы: зонная пластинка увеличивает освещенность, действуя подобно собирающей линзе. [ m= 0, 2, 4,… для прозрачных и m=1, 3, 5,… для непрозрачных колец].

<9 10 111213 14 15 >

Дата добавления: 2017-11-21; просмотров: 1210;