Свойство изолированной (от внешнего воздействия) материальной точки сохранять скорость - называется инертностью или инерцией.

Законы динамики. Дифференциальные уравнения движения материальной точки.

Напоминаю, что объектом изучения статики являлось абсолютно твердое тело, находящееся в состоянии равновесия.

В кинематике мы изучали движение материальных объектов с геометрической точки зрения без учета масс и действующих на них сил.

Но не рассматривали, почему, то или иное тело так движется.

А теперь мы приступаем к изучению динамики, будем рассматривать движение, но уже с учетом действующих сил.

Динамика последний раздел курса теоретической механики. В этом разделе

Решаются самые общие задачи движения материального объекта.

Как и в кинематике, динамику подразделяют на два больших раздела:

- динамику материальной точки;

- динамику системы материальных точек и материального тела.

Начнем мы с изучения движения материальной точки, а затем уже перейдем к системе МТ.

Формулировка.

Динамика ― раздел теоретической механики, в котором движение изучается в зависимости от действующих сил и начального состояния.

В динамике будут решаться уравнения второго порядка и основные действия, которые необходимо будет выполнять - интегрирование

1. Основные законы динамики.

В основе динамики лежат известные вам законы Ньютона и изложенные им на латинском языке в трактате"Математические начала натуральной философии" (1687).

Сочинение Ньютона переведено на русский язык академиком А.Н.Крыловым (Известия морской академии, 1915; перепечатано в Собрании трудов акад. А.Н.Крылова, т. VII изд. АН СССР, 1936)

Законы Ньютона справедливы для тела, которое представляет собой свободную материальную точку.

Первый закон (закон инерции).

Формулировка

Изолированная от внешних воздействий материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенная сила не заставит её изменить это состояние.

Свойство изолированной (от внешнего воздействия) материальной точки сохранять скорость - называется инертностью или инерцией.

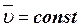
Согласно данному закону при движении материальной точки по инерции приложение силы не требуется.

Сама точка не может изменить свою скорость; скорость изменится только при действии на неё силы.

Другими словами, приобрести то или иное ускорение точка может только от внешнего воздействия.

В этой формулировке отсутствует очень важный момент, не указанна система отсчета.

Возникает вопрос.

Существует ли такая система отсчета, в которой справедлив закон динамики?

Как механики на этот вопрос отвечают?

Дают такое определение:

Систему отсчета, в которой выполняются закон инерции, - называется инерциальной или галлилеевой, а затем постулируют (воспринимают) существование такой системы и считают ее условно неподвижной.

Т. к. вам придется заниматься задачами динамики, которые происходят вблизи поверхности земли или на земле, в этом случае в качестве инерциальной системы берут так называемую земную (геоцентрическую)систему.

Угловая скорость вращения земли очень маленькая, поэтому можно ею пренебречь.

Это означает, что движением земли пренебрегают (движением вокруг оси и движением вокруг Солнца) и считают систему жестко связанную с землей системой инерциальной.

Это не значит, что такая система всегда может быть рассмотрена как инерциальная.

При решении задач космонавтики и астрономии:

В качестве инерциальной системы отсчета принимают гелеоценрическую (солнечную) систему отсчета, в которой данный закон выполняется с весьма высокой точностью.

В центре масс солнца помещают начало координат, а оси направляют к трем звездам, которые практически не меняют свое положение.

В северном полушарии левые берега размыты сильнее. Почему?

Это объясняется вращением земли. Скорость вращения земли маленькая, но реки текут веками. Возникает ускорение Кориолиса, которое приводит к тому, что правые берега размываются сильнее.

У железной дороги в северном полушарии все правые рельсы стерты сильнее, чем левые. Объясняется тоже вращением земли.

Но в большинстве случаев эту систему можно считать инерциальной.

Таких систем существует бесчисленное множество. Все системы, которые движутся поступательно и равномерно по отношению к первой системе тоже будут инерциальными.