Основные законы распределения дискретных и непрерывных случайных величин (биномиальный, геометрический, нормальный, показательный, равномерное распределение).

2.1. Биноминальное распределение.

Если производится п независимых испытаний, в каждом из которых событие А может появиться с одинаковой вероятностью р в каждом из испытаний, то вероятность того, что событие не появится, равна q = 1 – p.

Примем число появлений события в каждом из испытаний за некоторую случайную величину Х.

Чтобы найти закон распределения этой случайной величины, необходимо определить значения этой величины и их вероятности.

Значения найти достаточно просто. Очевидно, что в результате п испытаний событие может не появиться вовсе, появиться один раз, два раза, три и т.д. до п раз.

Вероятность каждого значения этой случайной величины можно найти по формуле Бернулли.

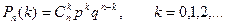
Эта формула аналитически выражает искомый закон распределения. Этот закон распределения называется биноминальным.

Пример. В партии 10% нестандартных деталей. Наугад отобраны 4 детали. Написать биноминальный закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения.

Вероятность появления нестандартной детали в каждом случае равна 0,1.

Найдем вероятности того, что среди отобранных деталей:

1) Вообще нет нестандартных.

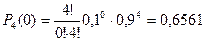
2) Одна нестандартная.

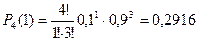
3) Две нестандартные детали.

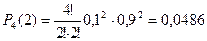
4) Три нестандартные детали.

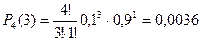
5) Четыре нестандартных детали.

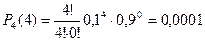
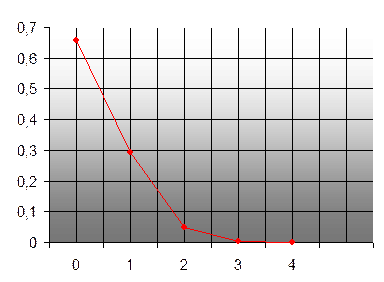Построим многоугольник распределения.

Пример. Две игральные кости одновременно бросают 2 раза. Написать биноминальный закон распределения дискретной случайной величины Х – числа выпадений четного числа очков на двух игральных костях.

Каждая игральная кость имеет три варианта четных очков – 2, 4 и 6 из шести возможных, таким образом, вероятность выпадения четного числа очков на одной кости равна 0,5.

Вероятность одновременного выпадения четных очков на двух костях равна 0,25.

Вероятность того, что при двух испытаниях оба раза выпали четные очки на обеих костях, равна:

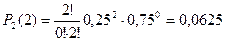
Вероятность того, что при двух испытаниях один раз выпали четные очки на обеих костях:

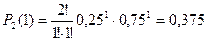
Вероятность того, что при двух испытаниях ни одного раза не выпаде четного числа очков на обеих костях:

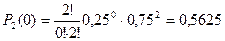
2.2. Распределение Пуассона. (Симеон Дени Пуассон (1781 – 1840) – французский математик)

Пусть производится п независимых испытаний, в которых появление события А имеет вероятность р. Если число испытаний п достаточно велико, а вероятность появления события А в каждом испытании мало (p£0,1), то для нахождения вероятности появления события А k раз находится следующим образом.

Сделаем важное допущение – произведение пр сохраняет постоянное значение:

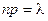
Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном п) остается неизменным.

По формуле Бернулли получаем:

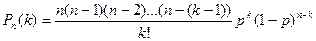
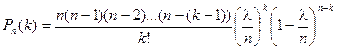
Найдем предел этой вероятности при п®¥.

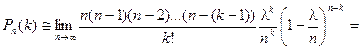
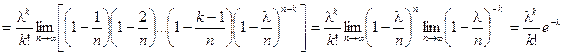
Получаем формулу распределения Пуассона:

Если известны числа l и k, то значения вероятности можно найти по соответствующим таблицам распределения Пуассона.

2.3. Равномерное распределение.

Непрерывная случайная величина имеет равномерноераспределение на отрезке [a, b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю.

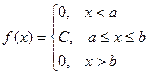
Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения.

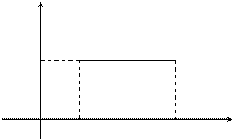f(x)

0 a b x

Получаем .

Найдем функцию распределения F(x) на отрезке [a,b].

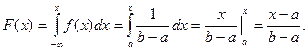
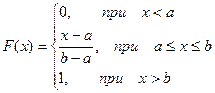
F(x)

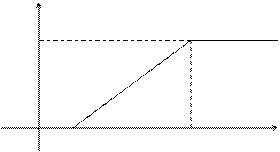
0 a b x

Для того, чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.

Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения.

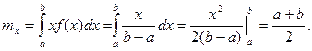
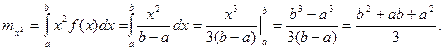
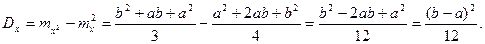
Вероятность попадания случайной величины в заданный интервал:

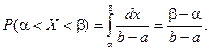
2.4. Показательное распределение.

Показательным (экспоненциальным)называется распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью

где l - положительное число.

Найдем закон распределения.

Графики функции распределения и плотности распределения:

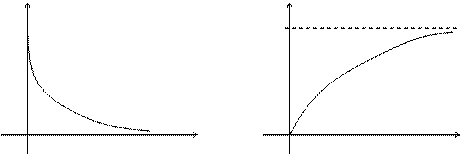f(x) F(x)

l 1

0 x 0 x

Найдем математическое ожидание случайной величины, подчиненной показательному распределению.

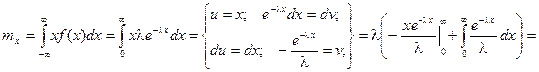
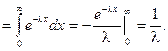
Результат получен с использованием того факта, что

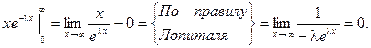
Для нахождения дисперсии найдем величину М(Х²).

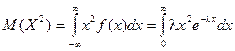
Дважды интегрируя по частям, аналогично рассмотренному случаю, получим:

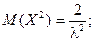
Тогда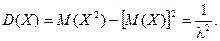

Итого:

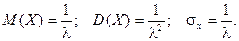
Видно, что в случае показательного распределения математическое ожидание и среднее квадратическое отклонение равны.

Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал.

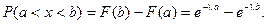
Показательное распределение широко используется в теории надежности.

Допустим, некоторое устройство начинает работать в момент времени t₀=0, а через какое– то время t происходит отказ устройства.

Обозначим Т непрерывную случайную величину – длительность безотказной работы устройства.

Таким образом, функция распределения F(t) = P(T<t) определяет вероятность отказа за время длительностью t.

Вероятность противоположного события (безотказная работа в течение времени t) равна R(t) = P(T>t) = 1 – F(t).

Функцией надежностиR(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.

Часто на практике длительность безотказной работы подчиняется показательному закону распределению.

Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.

Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.

Функция надежности для какого- либо устройства при показательном законе распределения равна:

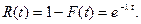
Данное соотношение называют показательным законом надежности.

Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.

Таким образом, безотказная работа устройства зависит только от интенсивности отказов l и не зависит от безотказной работы устройства в прошлом.

Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.

2.5. Нормальный закон распределения.

Нормальнымназывается распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

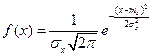
Нормальный закон распределения также называется законом Гаусса.

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Можно легко показать, что параметры 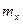и 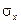, входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.

Найдем функцию распределения F(x).

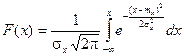
График плотности нормального распределения называется нормальной кривойили кривой Гаусса.

Нормальная кривая обладает следующими свойствами:

1) Функция определена на всей числовой оси.

2) При всех х функция распределения принимает только положительные значения.

3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.

4) Найдем экстремум функции.

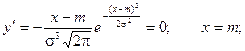
Т.к. при y’ > 0 при x < m и y’ < 0 при x > m , то в точке х = т функция имеет максимум, равный .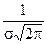

5) Функция является симметричной относительно прямой х = а, т.к. разность

(х – а) входит в функцию плотности распределения в квадрате.

6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.

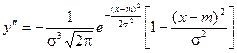
При x = m + s и x = m - s вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.

В этих точках значение функции равно .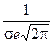

Построим график функции плотности распределения.

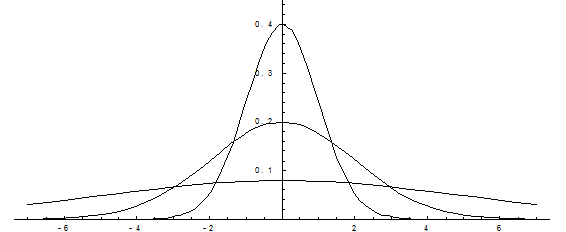
Построены графики при т =0 и трех возможных значениях среднего квадратичного отклонения s = 1, s = 2 и s = 7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается..

Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.

При а = 0 и s = 1 кривая называется нормированной. Уравнение нормированной кривой:

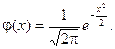
Лекция № 3

Тема: Распределения случайных величин

План:

1. Функция, плотность распределения.

2. Числовые характеристики (математическое ожидание, дисперсия, среднее квадратическое отклонение, мода, медиана).

<5 6 789 10 11 >

Дата добавления: 2019-12-09; просмотров: 766;

Поиск по сайту

Узнать еще