Для количественного сравнения событий по степени возможности их появления вводится числовая мера, которая называется вероятностью события.

Вероятность события А равна отношению числа случаев т, благоприятствующихему, к числу п - общму числу случаев (единственно возможных, равновозможных и несовместных). Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А:

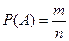- классическое определение вероятности.

Это есть Из формулы следует, что вероятность события является неотрицательным числом и может изменяться в пределах от нуля до единицы в зависимости от того, какую долю составляет благоприятствующее число случаев от общего числа случаев: 0 ≤ т ≤ п, .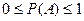

Таким образом, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, найти совокупность единственно возможных, равновозможных и несовместных случаев, подсчитать общее их число п, число случаев т, благоприятствующих данному событию, и затем выполнить расчет по формуле.

Свойства классической вероятности:

1. Если все случаи являются благоприятствующими данному событию 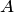, то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления Р(А) = 1, так как в этом случае т = п:

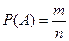= 1

2. Если нет ни одного случая, благоприятствующего данному событию 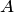, то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления Р(А) = 0, так как в этом случае :

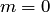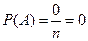
3. Вероятность наступления событий, образующих полную группу, равна единице.

4. Вероятность наступления противоположного события, которое обозначается символом 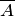, определяется:

Р(А)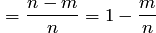

где 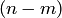- число случаев, благоприятствующих появлению противоположного события 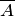. Отсюда вероятность наступления противоположного события 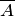равна разнице между единицей и вероятностью наступления события :

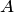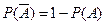
Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.

Пример. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.

Решение. Обозначим 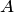событие, состоящее в том, что набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных исходов равно 10. Эти исходы единственно возможны (одна из цифр набрана обязательно) и равновозможны (цифра набрана наудачу). Благоприятствует событию 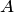лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:

.

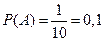Пример. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым.

Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С.

Тогда в соответствием с записанными выше формулами получаем:

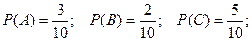
Отметим, что вероятность наступления одного из двух попарно несовместных событий равна сумме вероятностей этих событий.

Но классический метод определения вероятности случайного события довольно относительный, так как на практике сложно представить результат опыта в виде совокупности элементарных событий, доказать, что события равновероятные.

Например, при произведении опыта с подбрасыванием монеты на результат опыта могут влиять такие факторы как несимметричность монеты, влияние ее формы на аэродинамические характеристики полета, атмосферные условия и т.д.

Классический метод определения вероятности неприменимк испытаниям с бесконечным числом исходовпо двум причинам: во-первых, классическое определение вероятности предполагает, что общее число случаев 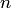должно быть конечно. На самом же деле оно зачастую не ограничено. Во-вторых, часто невозможно представить исходы опыта в виде равновозможных и несовместных событий.

Следовательно, необходимо использовать другие методы вычисления вероятностей.