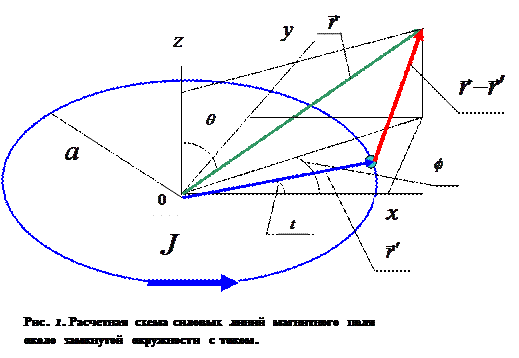
Силовые линии магнитного поля плоского контура с током в форме окружности.
Пусть по окружности радиуса  , расположенной в плоскости
, расположенной в плоскости 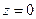 декартовой ситемы координат (центр окружности совпадает с началом координат) течёт электрический ток
декартовой ситемы координат (центр окружности совпадает с началом координат) течёт электрический ток 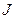 (рис. 1). Декартовы координаты произвольной точки пространства М (точки наблюдения) запишем через сферические координаты
(рис. 1). Декартовы координаты произвольной точки пространства М (точки наблюдения) запишем через сферические координаты 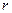 ,
, 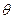 и
и 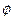 :
:
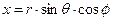 ,
, 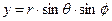 ,
, 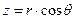 . (1)
. (1)
Координаты точки расположения элемента контура с током имеют вид:
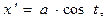
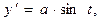
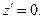 (2)
(2)
Выпишем выражения для проекций элемента контура с током на направления координатных осей декартовой системы координат
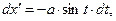
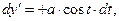
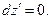 (3)
(3)
Расстояние между точкой расположения элемента контура с током и точкой наблюдения описывается зависимостью
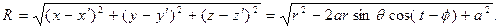 (4)
(4)
Располагая приведенными выше зависимостями и используя дифференциальную форму закона Био-Савара-Лапласа и принцип суперпозиции, можно получить выражения для компонент вектора магнитной индукции в произвольной точке пространства:
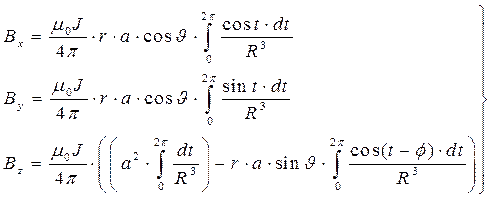 ( 5)
( 5)
|
Анализ полученных формул (переменная 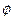 встречается в них только в комбинации с переменной
встречается в них только в комбинации с переменной 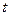 в форме разности) и пространственной конфигурации контура с током (осевая симметрия) позволяет провести вычисления квадратур при значении переменной
в форме разности) и пространственной конфигурации контура с током (осевая симметрия) позволяет провести вычисления квадратур при значении переменной 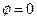 , а потом распространить получаемые результаты на произвольное значение
, а потом распространить получаемые результаты на произвольное значение 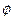 . Использование математической системы символьных вычислений MAPLE позволяет получить замкнутые аналитические зависимости для выписанных квадратур, они имеют достаточно громоздкую форму и содержат специальные функции математической физики – эллиптические интегралы первого и второго рода. Для дальнейшего достаточно знать, что полученные зависимости действительно позволяют вычислить численные значения описанных выше квадратур. Более того, в системе символьных вычислений MAPLE эта операция выполняется также просто, как и вычисление тригонометрических функций. Ниже будем предполагать, что имеют место явные выражения
. Использование математической системы символьных вычислений MAPLE позволяет получить замкнутые аналитические зависимости для выписанных квадратур, они имеют достаточно громоздкую форму и содержат специальные функции математической физики – эллиптические интегралы первого и второго рода. Для дальнейшего достаточно знать, что полученные зависимости действительно позволяют вычислить численные значения описанных выше квадратур. Более того, в системе символьных вычислений MAPLE эта операция выполняется также просто, как и вычисление тригонометрических функций. Ниже будем предполагать, что имеют место явные выражения
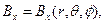
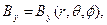
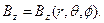 (6)
(6)
Обратим внимание читателя на характерное свойство рассматриваемого магнитного поля
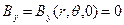 . (7)
. (7)
Этот результат свидетельствует о том, что силовая линия магнитного поля, проходящая через точку пространства с азимутальной координатой 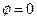 целиком лежит в плоскости, описываемой этим условием, а условие осевой симметрии распределения тока в пространстве позволяет заключить, что силовая линия магнитного поля при произвольном значении азимутальной координаты будет идентична аналогичной линии в рассматриваемой плоскости.
целиком лежит в плоскости, описываемой этим условием, а условие осевой симметрии распределения тока в пространстве позволяет заключить, что силовая линия магнитного поля при произвольном значении азимутальной координаты будет идентична аналогичной линии в рассматриваемой плоскости.
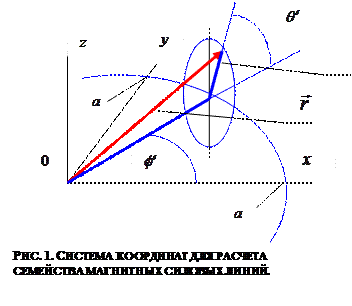
Успех построения семейства силовых линий рассматриваемого магнитного поля во многом определяется выбором метода параметризации пространственной, в данном случае плоской кривой. 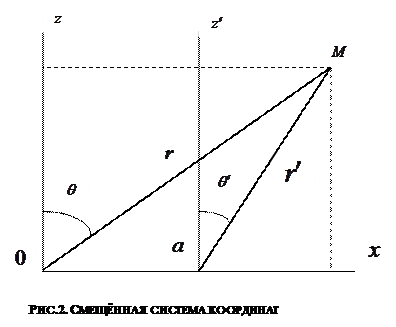 Введем показанную на рис. 2 смещенную систему координат. Прямая линия 0х является «следом» плоскости окружности , по которой течёт электрический ток. Точка 0 на этой линии соответствует положению оси симметрии описанной окружности. Точка а является «следом» окружности, величина
Введем показанную на рис. 2 смещенную систему координат. Прямая линия 0х является «следом» плоскости окружности , по которой течёт электрический ток. Точка 0 на этой линии соответствует положению оси симметрии описанной окружности. Точка а является «следом» окружности, величина 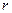 описывает расстояние от начала координат исходной системы до точки наблюдения М, а величина
описывает расстояние от начала координат исходной системы до точки наблюдения М, а величина 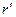 - расстояние от окружности с током до точки наблюдения М в плоскости
- расстояние от окружности с током до точки наблюдения М в плоскости 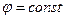 (рис.1). Углы
(рис.1). Углы 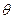 и
и 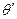 , показанные на рис.2, отсчитываются от соответствующих вертикальных параллельных друг другу осей по часовой стрелке. Легко видеть, что имеют место соотношения:
, показанные на рис.2, отсчитываются от соответствующих вертикальных параллельных друг другу осей по часовой стрелке. Легко видеть, что имеют место соотношения:
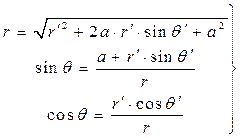 (8)
(8)
Удобство такого перехода состоит в том, что, по-видимому, силовая линия будет огибать точку 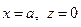 . В этом случае естественным параметром силовой линии является координата
. В этом случае естественным параметром силовой линии является координата 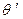 , её изменение в пределах от
, её изменение в пределах от 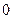 до
до 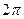 позволяет описать все точки плоской замкнутой кривой.
позволяет описать все точки плоской замкнутой кривой.
Дифференциальные уравнения силовой линии в форме (1) раздела 6.3 записаны в декартовой системе координат. В силу соотношений (8) имеем
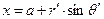 ,
, 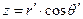 , (9)
, (9)

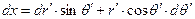 ,
, 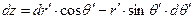 . (10)
. (10)
Замечая, что 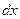 и
и 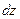 связаны между собой описанными выше условиями, а дифференциал
связаны между собой описанными выше условиями, а дифференциал 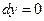 , разрешаем систему уравнений (9)-(10) относительно дифференциала
, разрешаем систему уравнений (9)-(10) относительно дифференциала 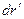 :
:
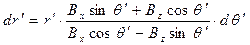 . (11)
. (11)
Тем самым мы получили уравнение силовой линии в смещенной системе координат. Если задать начальное значение 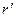 и начальное значение
и начальное значение 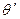 , то с помощью уравнения (11) получим при заданной величине
, то с помощью уравнения (11) получим при заданной величине 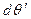 приращение координаты
приращение координаты 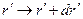 и координаты
и координаты 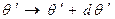 . Повторяя описанную процедуру, получим последовательно координаты силовой линии.
. Повторяя описанную процедуру, получим последовательно координаты силовой линии.
На рис.3. приведены результаты реализации описанной выше процедуры построения силовых линий магнитного поля для рассматриваемого случая. На графике сохранены пропорции геометрического построения. На рисунке 3 помечены «следы» тонкого кругового кольца, по которому течёт электрический ток. В левой точке (-1,0) электрический ток течёт «на нас», а в правой точке (+1,0) – «от нас», семейство силовых линий в левой части рисунка является зеркальным отражением семейства силовых линий в правой части относительно оси 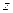 (ось симметрии рассматриваемой конфигурации электрического тока).
(ось симметрии рассматриваемой конфигурации электрического тока).
|
При анализе семейства силовых линий магнитного поля следует обратить внимание на характерное свойство силовых линий кругового витка с током: они являются замкнутыми и не пересекают друг друга. Небольшое несовпадение начальной и конечной точки удаленной силовой линии на приведенном рисунке зависит от точности счёта, уменьшение погрешности вычислений теоретически сводит к нулю описанную разницу. Cемейство силовых линий содержит одну линию, лежащую на оси симметрии системы: она «начинается» в нижней бесконечно удаленной точке и «заканчивается» в верхней бесконечно удаленной точке. Иногда говорят, что эта силовая линия замыкается на себя «через бесконечность». Линий, начинающихся или заканчивающихся в конечной области пространства, рассматриваемое семейство не содержит.
6.3.3. Силовые линии магнитного поля совокупности прямолинейного и кругового токов.
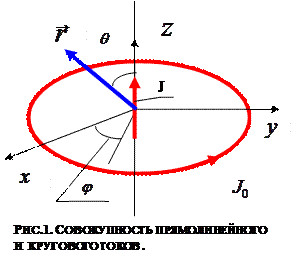 Рассмотрим систему электрических токов, текущих по тонким проводникам, показанным на рис. 1. Пусть прямолинейный ток
Рассмотрим систему электрических токов, текущих по тонким проводникам, показанным на рис. 1. Пусть прямолинейный ток 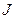 начинается в нижней бесконечно удаленной точке и заканчивается в верхней бесконечно удаленной точке, а плоскость окружности с током
начинается в нижней бесконечно удаленной точке и заканчивается в верхней бесконечно удаленной точке, а плоскость окружности с током 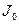 перпендикулярна прямолинейному току и центр окружности лежит на прямой, по которой течет ток
перпендикулярна прямолинейному току и центр окружности лежит на прямой, по которой течет ток 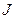 . Расположение декартовой и сферической систем координат показано на рис. 1.
. Расположение декартовой и сферической систем координат показано на рис. 1.
Известно, что магнитные поля от первого и второго тока можно рассчитать отдельно и потом сложить по правилу сложения векторов. Система токов, приведенная на рис.1 привлекательна тем, что позволяет воспользоваться уже полученными выше результатами и, вместе с тем, обнаружить новые свойства семейства магнитных силовых линий, которые не упоминаются в элементарном курсе физики и не всегда обсуждаются в распространенных учебниках по общему курсу физики.
Итак, дифференциальные уравнения силовой линии магнитного поля (1) раздела 6.3 должны теперь рассматриваться с учетом соотношений (1)-(4) раздела 6.3.1, описывающих распределение поля магнитной индукции от прямолинейного тока бесконечной протяженности и соотношений (5) раздела 6.3.2, описывающих распределение поля магнитной индукции от кругового тока. Для обеспечения однородности формы записи результирующего магнитного поля необходимо использовать в формулах (1)-(4) раздела 6.3.1 соотношения (1) раздела 6.3.2 для перехода к переменным сферической системы координат. После выполнения указанных действий мы располагаем аналитическими зависимостями
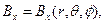
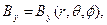
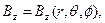 (1)
(1)
|
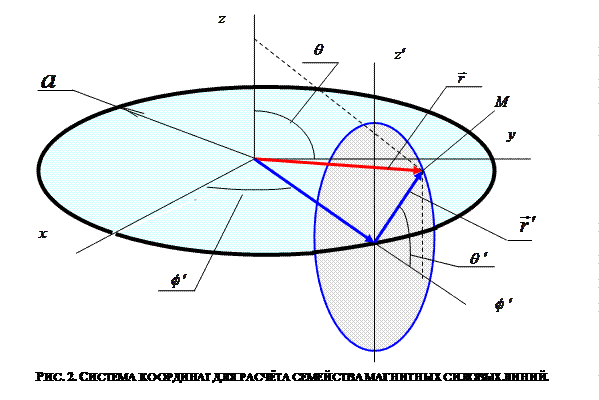
подробно. Связь сферических и тороидальных координат точки наблюдения М (т.е. произвольной точки силовой линии) описывается соотношениями:
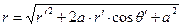 ,
, 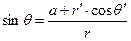 ,
, 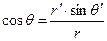 ,
, 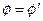 . (2)
. (2)
Связь декартовых и тороидальных координат имеет вид
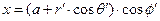 ,
, 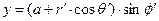 ,
, 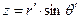 . (3)
. (3)
Для соответствующих дифференциалов поучаем зависимости
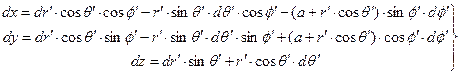 (4)
(4)
Соотношения (4) рассматриваем как систему уравнений для определения дифференциалов тороидальных координат, её решение имеет вид:
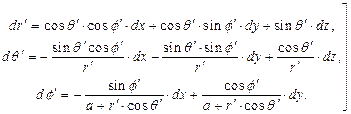 (5)
(5)
В последнюю из зависимостей (5) подставим условие существования силовой линии
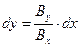 (6)
(6)
и выразим 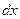 через
через 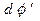 , после чего можно записать выражения для дифференциалов
, после чего можно записать выражения для дифференциалов 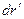 и
и 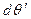 как линейных функций дифференциала
как линейных функций дифференциала 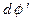 . Эти соотношения имеют вид:
. Эти соотношения имеют вид:
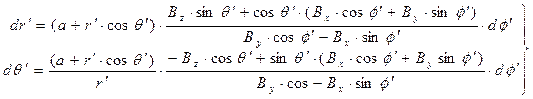 (7)
(7)
что даёт возможность последовательного вычисления точек силовой линии
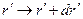 ,
, 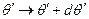 . (8)
. (8)
|
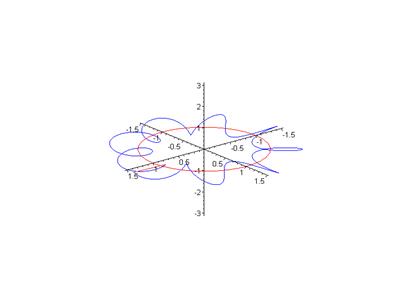
Рассматривая приведенный рисунок, на котором силовая линия в форме спирали навивается на некоторую поверхность тороида, следует обратить внимание на то, что при однократном полном обходе оси симметрии силовая линия не попала в исходную точку. При попытке продолжить построение силовой линии возможны два случая, либо замыкание силовой линии произойдет через конечное число обходов оси симметрии, либо такое замыкание просто невозможно при заданных параметрах системы токов и выбранном положении начальной точки силовой линии. Заметим, что условие замыкания связано с определенными условиями соизмеримости шага спирали и длины обхода. Меняя радиус тора, можно получить семейство вложенных друг в друга тороидальных поверхностей, причем только на некоторых из них условия соизмеримости окажутся выполненными. А что же происходит на остальных поверхностях? Силовая линия нигде не кончается, плотно заполняя «магнитную поверхность», при этом не пересекая саму себя! Подобное явление принципиально невозможно в электростатическом поле. Описанное свойство магнитных силовых линий находит практическое применение в устройствах для удержания заряженных частиц.
Заканчивая обсуждение раздела, заметим, что различие в характере поведения силовых линий электростатического и магнитостатического полей обусловлено разной природой источников поля, что находит отражение в системе основных уравнений электро- и магнитостатики.
Дата добавления: 2017-09-01; просмотров: 1863;

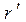
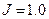 ,
, 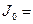 1.0 ,
1.0 , 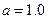 ).
).









