Практическое использование теоремы Гаусса.
Практическое использование интегральной формы теоремы Гаусса для вектора напряженности электростатического поля требует известной осторожности. Суть дела в том, что теорема Гаусса связывает между собой величину потока вектора напряжённости электростатического поля с суммарным зарядом внутри контрольной поверхности, а рассчитать желательно вектор  , который, в частности, не обязательно обращается в нуль при равенстве нулю потока вектора через контрольную поверхность. Эффективность использования интегральной формы теоремы Гаусса для расчёта напряженности электростатического поля заданного распределения электрических зарядов в рассматриваемой точке пространства зависит от того, удаётся ли провести через эту точку такую контрольную замкнутую поверхность, охватывающую выделенное распределение зарядов, для которой при некоторых оговоренных заранее физических условиях, наложенных на компоненты вектора
, который, в частности, не обязательно обращается в нуль при равенстве нулю потока вектора через контрольную поверхность. Эффективность использования интегральной формы теоремы Гаусса для расчёта напряженности электростатического поля заданного распределения электрических зарядов в рассматриваемой точке пространства зависит от того, удаётся ли провести через эту точку такую контрольную замкнутую поверхность, охватывающую выделенное распределение зарядов, для которой при некоторых оговоренных заранее физических условиях, наложенных на компоненты вектора  , возможно вычисление потока вектора
, возможно вычисление потока вектора  через эту поверхность. Более того, напряженность электростатического поля
через эту поверхность. Более того, напряженность электростатического поля  в рассматриваемой точке пространства должна достаточно просто входить в выражение для потока вектора
в рассматриваемой точке пространства должна достаточно просто входить в выражение для потока вектора  через контрольную поверхность. Для некоторых распределений электрических зарядов, обладающих высокой степенью пространственной симметрии, использование интегральной формы теоремы Гаусса для вектора напряженности электростатического поля поражает своей результативностью.
через контрольную поверхность. Для некоторых распределений электрических зарядов, обладающих высокой степенью пространственной симметрии, использование интегральной формы теоремы Гаусса для вектора напряженности электростатического поля поражает своей результативностью.
Практическое использование дифференциальной формы теоремы Гаусса для вектора напряжённости электростатического поля возможно, если a priori известны некоторые дополнительные соотношения между компонентами вектора напряжённости, позволяющие свести задачу расчёта к одному уравнению с одним неизвестным. Последнее может оказаться выполненным для системы электрических зарядов с высокой степенью пространственной симметрии. Но и при этом интегрирование упомянутого выше уравнения требует привлечения интегральной формы теоремы Гаусса для определения константы интегрирования. Это обстоятельство необходимо учитывать при выборе метода решения физической задачи, особенно при рассмотрении областей пространства с разными физическими свойствами или разделёнными заряженной поверхностью.
Ниже рассмотрим различные варианты практического использования теоремы Гаусса для расчёта вектора напряжённости электростатического поля в пространстве.
2.3.6.1. Напряженность электростатического поля, образованного одиночным сосредоточенным электрическим зарядом в вакууме.
В рассматриваемом случае электрический заряд достаточно поместить в центре сферы, проходящей через точку наблюдения, в которой необходимо определить величину и направление вектора напряженности электростатического поля  . Принятый вид контрольной поверхности обусловлен тем, что поле точечного заряда является центральным (т.е. сферически симметричным, количественные характеристики поля не зависят от угловых координат сферической системы координат), а контрольная поверхность описывается простым уравнением
. Принятый вид контрольной поверхности обусловлен тем, что поле точечного заряда является центральным (т.е. сферически симметричным, количественные характеристики поля не зависят от угловых координат сферической системы координат), а контрольная поверхность описывается простым уравнением 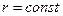 , где
, где 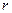 - радиальная координата точки наблюдения. Внешняя нормаль к элементу контрольной поверхности направлена по радиусу, это направление совпадает с направлением вектора напряжённости. В силу симметрии нормальная компонента вектора напряженности везде одинакова для точек контрольной поверхности. В этом случае поток вектора
- радиальная координата точки наблюдения. Внешняя нормаль к элементу контрольной поверхности направлена по радиусу, это направление совпадает с направлением вектора напряжённости. В силу симметрии нормальная компонента вектора напряженности везде одинакова для точек контрольной поверхности. В этом случае поток вектора  через контрольную поверхность равен произведению
через контрольную поверхность равен произведению 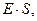 где S - площадь поверхности сферы радиуса
где S - площадь поверхности сферы радиуса 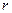 . Приравняем полученное выражение величине электрического заряда внутри контрольной поверхности, деленной на величину электрической постоянной, и получим зависимость модуля напряженности электростатического поля точечного заряда от расстояния до точки наблюдения:
. Приравняем полученное выражение величине электрического заряда внутри контрольной поверхности, деленной на величину электрической постоянной, и получим зависимость модуля напряженности электростатического поля точечного заряда от расстояния до точки наблюдения:
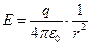 . (1)
. (1)
Не представляет труда выписать и выражение для вектора напряженности рассматриваемого поля
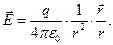 (2)
(2)
Если сосредоточенный электрический заряд помещен в точке пространства с координатами 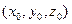 , предыдущее выражение принимает вид
, предыдущее выражение принимает вид
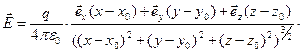 (3)
(3)
Здесь x, y, z – координаты точки наблюдения, 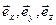 - орты декартовой системы координат.
- орты декартовой системы координат.
Для расчёта напряженности электростатического поля одиночного сосредоточенного заряда возможно использование дифференциальной формы теоремы Гаусса в сферической системе координат:
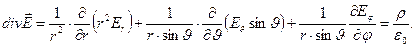 (4)
(4)
По условию сосредоточенный электрический заряд 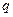 помещён в начало сферической системы координат. Сферически симметричное расположение заряда обуславливает обращение в нуль компонент
помещён в начало сферической системы координат. Сферически симметричное расположение заряда обуславливает обращение в нуль компонент 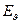 и
и 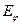 . Объёмная плотность электрического заряда вне начала координат равна нулю. Радиальная компонента напряженности рассматриваемого электростатического поля удовлетворяет уравнению
. Объёмная плотность электрического заряда вне начала координат равна нулю. Радиальная компонента напряженности рассматриваемого электростатического поля удовлетворяет уравнению
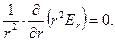 (5)
(5)
Интегрирование этого уравнения приводит к соотношению
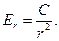 (6)
(6)
Постоянную интегрирования С необходимо положить равной 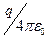 в соответствии с интегральной формой теоремы Гаусса.
в соответствии с интегральной формой теоремы Гаусса.
2.3.6.2. Напряжённость электростатического поля, образованного электрическими зарядами, равномерно распределёнными по поверхности сферы.
Если необходимо рассчитать напряжённость электростатического поля, образованного электрическими зарядами, равномерно расположенными по поверхности сферы конечных размеров с центром в начале координат с использованием теоремы Гаусса, то целесообразно отдельно рассмотреть электростатическое поле внутри и снаружи равномерно заряженной сферы. Напряжённость электростатического поля внутри равномерно заряженной сферы равна нулю. Это заключение следует из того факта, что в условиях сферической симметрии распределения зарядов, образующих поле, на контрольной сферической поверхности с центром в начале координат нормальная компонента вектора напряжённости везде одинакова. Поток вектора напряженности через контрольную поверхность 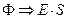 следует приравнять нулю: зарядов внутри контрольной поверхности нет. Поскольку величина площади контрольной поверхности не равна нулю, то нормальная компонента вектора напряженности должна быть равной нулю. Касательная к контрольной поверхности составляющая вектора напряжённости должна обращаться в нуль, иначе в рассматриваемой физической ситуации нарушалось бы свойство потенциальности электростатического поля (эта особенность электростатического поля будет изучена в разделе 2.4 настоящего пособия).
следует приравнять нулю: зарядов внутри контрольной поверхности нет. Поскольку величина площади контрольной поверхности не равна нулю, то нормальная компонента вектора напряженности должна быть равной нулю. Касательная к контрольной поверхности составляющая вектора напряжённости должна обращаться в нуль, иначе в рассматриваемой физической ситуации нарушалось бы свойство потенциальности электростатического поля (эта особенность электростатического поля будет изучена в разделе 2.4 настоящего пособия).
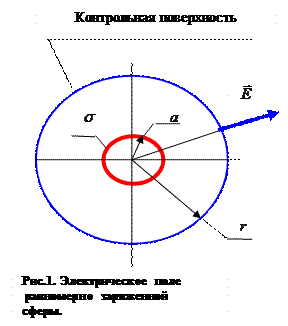 Напряжённость электростатического поля вне равномерно заряжённой сферы, очевидно, обладает сферической симметрией. Её радиальная компонента сохраняет постоянное значение на сферической контрольной поверхности произвольного радиуса
Напряжённость электростатического поля вне равномерно заряжённой сферы, очевидно, обладает сферической симметрией. Её радиальная компонента сохраняет постоянное значение на сферической контрольной поверхности произвольного радиуса 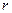 с центром в начале координат и является нормальной составляющей вектора к элементам контрольной поверхности. Поток вектора напряжённости электростатического поля через замкнутую контрольную поверхность равен произведению величины Е на площадь контрольной поверхности
с центром в начале координат и является нормальной составляющей вектора к элементам контрольной поверхности. Поток вектора напряжённости электростатического поля через замкнутую контрольную поверхность равен произведению величины Е на площадь контрольной поверхности 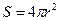 . В соответствии с интегральной теоремой Гаусса поток вектора
. В соответствии с интегральной теоремой Гаусса поток вектора  через контрольную поверхность следует приравнять суммарному заряду внутри контрольной поверхности, деленному на электрическую постоянную:
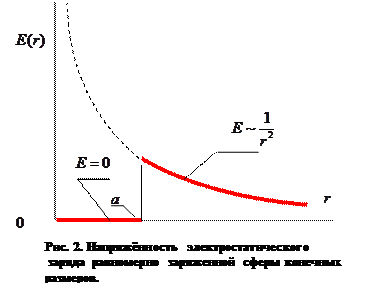
через контрольную поверхность следует приравнять суммарному заряду внутри контрольной поверхности, деленному на электрическую постоянную:
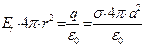 , (1)
, (1)
 здесь
здесь 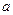 - радиус заряженной сферы,
- радиус заряженной сферы, 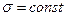 - поверхностная плотность электрического заряда. В итоге получаем зависимость:
- поверхностная плотность электрического заряда. В итоге получаем зависимость: 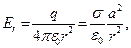
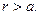 (2)
(2)
Из полученного результата следует, что поле вне равномерно заряженной сферы совпадает с полем одиночного сосредоточенного заряда, равного заряду сферы и расположенного в её центре. Кроме того, предел полученного выражения при стремлении точки наблюдения к поверхности заряженной сферы равен 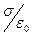 . Если учтём, что напряжённость электростатического поля внутри равномерно заряженной сферы равна нулю, приходим к известному соотношению:
. Если учтём, что напряжённость электростатического поля внутри равномерно заряженной сферы равна нулю, приходим к известному соотношению:
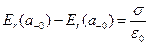 , (3)
, (3)
справедливость которого выше доказана в общем случае. Графическая иллюстрация полученных результатов приведена на рис. 2.
Общая методика использования дифференциальной формы теоремы Гаусса в рассматриваемом случае практически не отличается от методики расчёта поля сосредоточенного заряда, только вспомогательное интегральное соотношение (теорему Гаусса) приходится рассматривать не в окрестности начала координат, а вблизи заряженной поверхности сферы радиуса 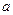 .
.
Дата добавления: 2017-09-01; просмотров: 1412;










