Объёмная плотность энергии.

В случае действительных величин объёмная плотность энергии электромагнитного поля определяется выражением:

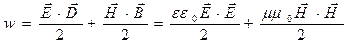. (7)

Если рассматривать векторы 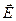и 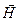как векторы с комплексными составляющими, то для получения действительного выражения для объёмной плотности энергии электромагнитного поля необходимо воспользоваться описанным выше приёмом:

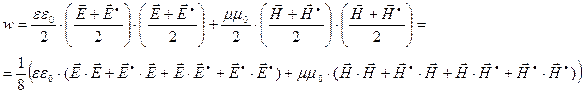(8)

Выражение (8) определяет «мгновенное» значение объёмной плотности электромагнитной энергии в рассматриваемой точке пространства, т.е. значение в некоторый момент времени t. Зависимость (8) представляет собой практически сумму квадратов действительных величин и поэтому является положительно определенной зависимостью. Её численные значения могут изменяться от нуля до некоторой максимальной величины. Представляет интерес вычисление средней по времени величины объёмной плотности энергии электромагнитного поля плоской волны. Средняя по времени физическая величина определяется по правилу:

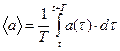. (9)

Для гармонических во времени процессов величину 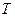выбирают равной периоду колебаний 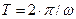, а начало отсчёта 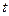выбирают равным нулю.

Легко видеть, что имеют место соотношения:

;

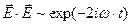
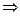
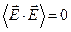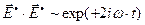
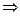
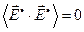; (10)

.

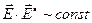
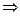
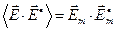Аналогичные результаты справедливы и для векторов напряжённости магнитного поля.

С учётом полученных результатов средняя по времени величина объёмной плотности энергии электромагнитного поля в рассматриваемой точке пространства может быть описана зависимостью

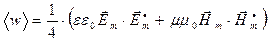. (11)

Выражение (11) является локальным, действительным и положительно определённым. С его помощью можно вычислить энергию электромагнитного поля в некоторой области пространства:

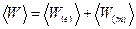, (12)

где энергия электрического поля и энергия магнитного поля определены соотношениями

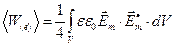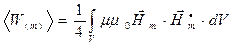, . (13)

Интегрирование в соотношениях (13) проводится по объёму рассматриваемой области пространства. Эти выражения ниже будут использованы при анализе балансовых энергетических соотношений.

Вектор Умова-Пойнтинга.

Плотность потока энергии электромагнитного поля, как известно, определяется выражением

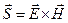. (14)

При необходимости использовать результаты метода комплексных амплитуд действительное (вещественное) выражение для вектора 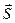записывают в виде:

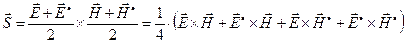. (15)

Оценивая векторные произведения в соотношении (15), получаем:

;

;

.

.

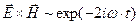
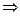
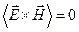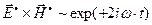
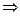
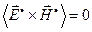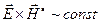
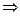
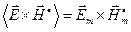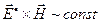
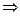
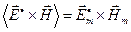В результате осреднения по времени зависимости (15) для мгновенного значения вектора плотности потока энергии приходим к соотношению:

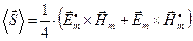. (16)

Таким образом, получают постоянную во времени векторную величину с вещественными компонентами. Интересно, что – формально - полученное выражение является действительной частью комплексного выражения

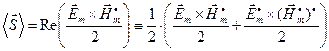. (17)

Это порождает возможность ввести в рассмотрение «комплексный вектор Умова-Пойнтинга»:

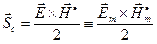. (18)

Обоснованием целесообразности такого приёма служит соотношение:

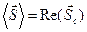. (19)

Физическое содержание соотношения (19) заключается в том, что среднее по времени от вектора плотности потока энергии электромагнитного поля в гармоническом приближении (вещественная постоянная векторная величина!) может быть вычислено как действительная часть комплексного вектора Умова-Пойнтинга.

Объёмная плотность мощности.

Для действительных величин объёмная плотность мощности вычисляется по выражению

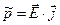. (20)

Выражение (20) – произведение двух гармонических величин - является нелинейным, поэтому для получения действительной величины в методе комплексных амплитуд требуется исходить из соотношения:

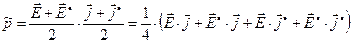. (21)

Зависимость (21) определяет действительное (вещественное) значение объёмной плотности мощности в произвольный момент времени. Поскольку рассматриваемая величина осциллирует во времени, можно ввести осреднённую по времени величину объёмной плотности мощности аналогично тому, как это было сделано выше при рассмотрении объёмной плотности энергии:

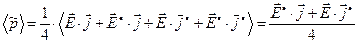. (22)

Анализ выражения (22) показывает, что можно ввести комплексную плотность мощности

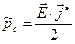, (23)

поскольку легко проверяется соотношение

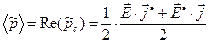. (24)

Теперь можно приступить к рассмотрению балансовых энергетических соотношений в неоднородной плоской электромагнитной гармонической волне.

Комплексный аналог теоремы Пойнтинга.

Уравнения Максвелла – уравнение электромагнитной индукции и уравнение полного тока в дифференциальной форме – запишем с использованием гармонического приближения:

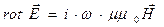, (25)

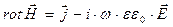. (26)

Заметим, что уравнения (25)-(26) справедливы, если форма зависимости гармонических величин от времени определена соотношениями (6).

Если 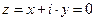, то имеет место 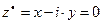, поскольку из первого уравнения следует 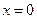и 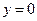. Другими словами говоря, если справедливо линейное уравнение для комплексной величины, то справедливо и комплексно сопряжённое уравнение. Воспользуемся этим математическим утверждением и запишем уравнение (26) в комплексно сопряжённой форме:

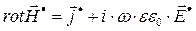. (27)

Умножим уравнение (25) скалярно на вектор 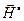, а уравнение (27) – на вектор :

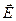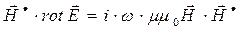, (28)

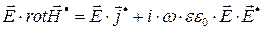. (29)

Вычтем из уравнения (28) уравнение (29):

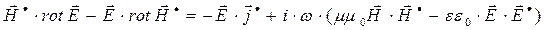. (30)

Левая часть уравнения (30) может быть преобразована:

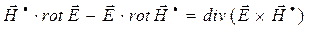. (31)

В принципе, здесь использовано известное векторное тождество, его можно проверить непосредственным вычислением в декартовой системе координат, а можно воспользоваться символическим методом и определением дифференциального векторного оператора «набла» (или оператора Гамильтона) . Продемонстрируем этот метод. Рассмотрим дивергенцию векторного произведения двух векторных полей:

.

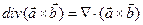Для того чтобы можно было пользоваться обозначением 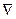как просто векторной величиной, перепишем предыдущее соотношение с учётом дифференциального характера оператора набла:

,

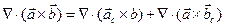где индексом «с» помечены условно постоянные величины, их можно «выносить» за символ дифференциального оператора 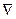. Теперь полученное выражение можно рассматривать просто как сумму двух смешанных произведений трёх векторов. Известно, что смешанное произведение трёх векторов может быть записано в нескольких эквивалентных формах. Нам необходимо выбрать такую форму, чтобы «вектор 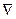» не оставался в крайней правой позиции: как дифференциальный оператор он должен на что-нибудь действовать:

, .

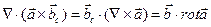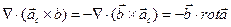Для установления справедливости соотношения (31) осталось только вместо произвольных векторных полей и подставить рассматриваемые векторы напряжённости электрического и магнитного поля.

Итак, установлено соотношение:

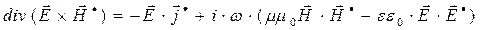. (32)

Вспоминая определения введённых выше комплексных величин, перепишем уравнение (32) в форме:

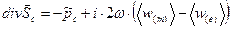, (33)

где

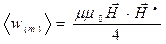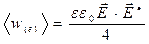, (34)

представляют собой средние по времени действительные положительные величины объёмной плотности магнитной и электрической энергии электромагнитного поля. Комплексный аналог теоремы Пойнтинга в дифференциальной форме получен.

Если воспользоваться математической теоремой Остроградского-Гаусса, можно получить и соответствующий интегральный аналог:

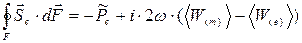, (35)

где 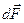- вектор, имеющий направление внешней нормали к элементу поверхности 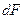и равный по модулю площади этого элемента, остальные обозначения встречались выше.

Выделяя в уравнении (35) действительную и мнимую части, получим:

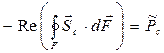, (36)

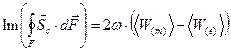. (37)

Уравнение (36) является балансовым соотношением для так называемой «активной» мощности: втекающий в рассматриваемый объём поток энергии (его вещественная часть!) равняется суммарной мощности потерь, в нашем случае – джоулевых потерь. Уравнение (37) фактически определяет так называемую «реактивную» мощность рассматриваемого объёма. В технических приложениях электродинамики оба понятия широко применяются. При конструировании и эксплуатации электротехнических устройств приходится заботиться о возможно наиболее эффективном уменьшении реактивной мощности устройств, обладающих электрической ёмкостью и индуктивностью.