Лекция №2. Диссоциация газов при высоких температурах с образованием атомов и радикалов
План:
1.Возбуждение атомов и молекул
2. Диссоциация молекул
3. Методы расчета диссоциации
Перехода газа в состояние плазмы происходит при содержании частиц или при их взаимодействии с излучением. При этом происходят процессы возбуждения и диссоциации атомов, ионизация и рекомбинация газов.
Возбуждение атома - это процесс перехода под воздействием подводимой энергии при поглощении фотонов или при столкновении с другими частицами электрона атома на более удаленную от ядра орбиту с возрастанием внутренней энергии. В возбужденном состоянии атом может пребывать долго (порядка 10-8 с). Возбуждение атома и молекулы происходит в результате поглощения энергии (Wn).
Wn=h•V=E1-E2 (2)
где h – постоянная планка = 6,6256•10-34Дж•с; V – частота перехода; E1 и E2 – энергии начальных и конечных уровней энергии атомной системы.
Атом имеет лишь три степени свободы, тогда как у многоатомных молекул степень свободы может быть больше. Кроме того, молекула может совершать вращательное движение, н атомы в молекуле могут колебаться вблизи своих равновесных положений. С каждой степенью свободы связанна определенная энергия. Энергия, связанная с первыми тремя степенями свободы, кинетическая, а с остальными степенями – внутренняя энергия молекулы. Атомы в молекуле удерживаются только силами кулоновского взаимодействия.
В связи между ними более или менее упругие. Атому можно придать колебательное движение с помощью внешней энергии (так называемой энергии возбуждения молекулы). Эта энергия очень мала, величина ее меньше, чем минимальная энергия возбуждения атому.
Если поглощенная молекулой энергия преобразованная в колебательную энергию атомов, очень, высока, то связи между атомами могут нарушится, а молекула может быть расщеплена на более простые частицы. Этот процесс называется диссоциация. Характерная величина энергии, необходимой для расщепления молекулы, называется энергией диссоциации. Продуктами диссоциации могут быть фрагментированные молекулы, возбужденные или ионизированные атомы.
При нагреве молекулы веществ распадаются на более простые частицы, т.е. происходит их диссоциация. Энергия диссоциации двухатомных молекул приведена в таблице 1
Таблица 1 - Энергия диссоциации двухатомных молекул.
| Молекула | Энергия диссоциации, эВ | Молекула | Энергия диссоциации, эВ | Молекула | Энергия диссоциации, эВ | Молекула | Энергия диссоциации, эВ |
| BaBr BaCl BaF BaH BaO BaS Br2 BrCl BrF BrO C2 CCl CF CH CN CO CaBr CaCl CaF CaH CaI CaO CaS Cl2 ClF ClO Cs2 CsBr CsCl | 2,8 2,7 3,8 1,8 4,7 2,4 1,97 2,23 2,4 2,4 6,2 2,8 4,7 3,47 8,4 11,1 2,9 2,8 3,1 1,7 2,8 5,0 3,0 2,48 2,6 2,8 0,45 4,3 4,4 | CsF CsH CsI Cu2 CuBr CuCl CuF CuH CuI CuO F2 H2 HD D2 HT T2 HBr HCl HF HI Hg2 HgBr HgCl HgF HgH HgI HgS I2 IBr | 5,0 1,9 3,6 0,2 3,4 3,7 3,0 2,9 3,0 4,8 1,6 4,48 4,51 4,55 4,52 4,59 3,75 4,43 5,9 3,05 0,06 0,7 1,0 1,8 0,38 0,36 2,8 1,54 1,82 | ICl IF IO K2 KBr KCl KF KH KI Li2 LiBr LiCl LiF LiH LiI LiO MgBr MgCl MgF MgH MgO N2 NBr Nh NO Ns Na2 NaBr NaCl | 2,15 2,9 1,9 0,51 3,95 4,4 5,1 1,86 3,33 1,1 4,4 4,8 6,0 2,4 3,6 3,4 3,2 3,9 5,0 2,2 3,4 9,76 2,9 3,6 6,5 5,0 0,73 3,8 4,2 | NaF NaH NaI NaK O2 OH Rb2 RbBr RbCl RbF RbH RbI S2 SH SO TlBr TlCl TlF TlH TlI ZnCl ZnH ZnI - - - - - - | 5,0 2,1 3,1 0,61 5,1 4,4 0,48 4,0 4,4 5,4 1,8 3,3 4,3 3,5 5,3 3,4 3,8 4,7 2,0 2,8 2,6 0,85 1,4 - - - - - - |
При температурах газовой атмосферы > 2500К, как показывают термодинамические расчеты и экспериментальные данные, необходимо учитывать присутствие в атмосфере заметных количеств атомарных частиц и радикалов. Так, в атмосфере, образующейся диссоциации водяного пара на молекулы H2 и O2 по реакции, обратной 2H2O 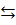 2H2 + O2 возможно образование атомов O и H, радикалов OH, частиц HO2. При температурах 2500 К они образуются в сверхравновесных количествах по цепным реакция воспламенения и горения, при высоких температура – по реакциям термической диссоциации молекулярных частиц H2, O2, H2O.
2H2 + O2 возможно образование атомов O и H, радикалов OH, частиц HO2. При температурах 2500 К они образуются в сверхравновесных количествах по цепным реакция воспламенения и горения, при высоких температура – по реакциям термической диссоциации молекулярных частиц H2, O2, H2O.
Наиболее термодинамически вероятным являются следующие реакции:
H2⇆2H; ∆H°298K = 436, 173 Дж/моль; (3)
O2⇆2O; ∆H°298K = 495,374 Дж/моль; (4)
H2O⇆OH +1/2H2; ∆H°298K = 260 828 Дж/моль (5)
H2O⇆2H+O (6)
Экспериментальное определение термодинамических характеристик этих реакций при очень высоких температурах, например калориметрическим методом, трудоемко и технически сложно. В связи с этим исключительное значение приобретают методами статистической термодинамики. Они позволяют с большой точностью определить термодинамические данные для одно и двухатомных части по результатам спектроскопических исследований. Они позволяют с большой точностью определить термодинамические данные для одно- и двухатомных частиц по результатам спектроскопических исследований. Так для реакции H2 = 2H найдено следующее выражение для Константы равновесия
КP = 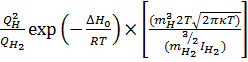
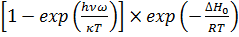 , (7)
, (7)
где QH и QH2- суммы состояний H и H2; m – масса частицы; h и k - постоянных Плана и Больцмана; IH2 – момент инерции молекулы H2; S – число симметрии, для H2 равное 2; v- частота колебаний ω – колебательное квантовое число, принимающее значения 0,1,2,3.
Для расчета по уравнению (6) можно принять следующие значения величин, найденные из спектроскопических данных 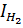 =0,467•10-10г/м3;
=0,467•10-10г/м3; 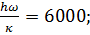 H°0 =430146±4180 Дж. Например, для 2000 К при использовании этих данных получают значение константы равновесия, равное Kр = 3,9.10-3.
H°0 =430146±4180 Дж. Например, для 2000 К при использовании этих данных получают значение константы равновесия, равное Kр = 3,9.10-3.
Аналогичным образом рассчитываются термодинамические характеристики других реакций диссоциации газов на атомы и радикалы, при помощи которых возможен расчет равновесного состава газовой атмосферы при температурах, когда атомные частицы и радикалы имеют значительные содержания и парциальные давления.
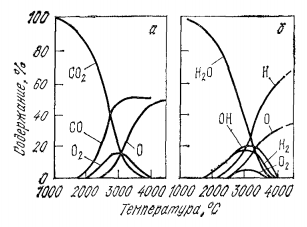
Рисунок 4. Температурная зависимость равновесного состава газовой фазы, образованной из CO2(a) и из H2O(б) до 4000°С
Результаты расчета показывают ( рис. 4), что уже при 3000°С и р = 101,325 Па концентрация одноатомных галлов H и O и радикала OH достигает одного порядка с молекулярным компонентами газовой фазы; кривые содержаний которых, а также OH проходят через максимумы. При 4000°С в газовой атмосфере преобладают H и O в соотношении близком к 2: 1, суммарное содержание других составляющих становится =10%
Другим способом расчета равновесного состава многокомпонентной газовой высокотемпературной атмосферы является определение экстремумов полных термодинамических функций. При этом нет необходимости подключать к расчету константы равновесия. Задача состоит в определении состава, при котором, например, энергия Гиббса единицы массы системы при заданных G°Пi, p и T достигает минимального значения, т.е:
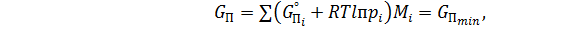 (8)
(8)
где G°П – стандартная энергия Гиббса; Mi – число молей i-го компонента в единицу массы системы.
При этом должны соблюдаться следующие дополнительные условия.
1.Закон сохранения вещества, выражаемый в обобщенном виде уравнением:
[Эj]= 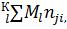 (9)
(9)
где [Эj] – число атомов элемента в единице массы системы:nji – атомов элемента i в j-м химическом веществе.
Число уравнений равно числу химических элементов m.
2. Уравнение Дальтона
p= 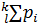 =
= 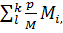 (10)
(10)
где М- общее число молей всех компонентов на единицу массы системы.
Для рещения уравнений () – () удобно ввести соотношения:
 11)
11)
и применить приведенную энергию Гиббса G*i = -G°i|T.
После этого определяется минимум функции
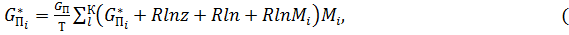 12)
12)
где 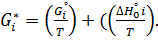
Для определения минимума функции и соответствующих к значений Mi и одного значения z при m условиях и одном условии используется метод Лагранжа. Составляется вспомогательная функция Л от к +m+2 переменных, в которых входят к неизвестных чисел Mi, величина z, m неопределенных множителей λi и один множитель λp. Эта функция имеет вид:
Л(M1,M2,…Mk,z,λi1,λi2,…λim,λp)= 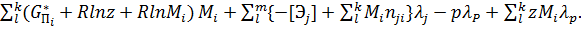
Дифференцирование этой функции по Mi,z,λj,λp дает уравнения
1. 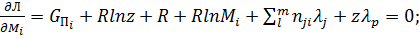 (13)
(13)
2.  (14)
(14)
3. 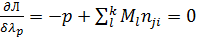 (15)
(15)
4. 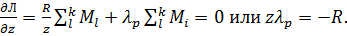 (16)
(16)
В связи с последним условием обобщённое уравнение производной
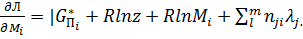 (17)
(17)
В качестве примера можно привести уравнении для расчета равновесного состава продуктов взаимодействия O2 и H2 (m=2) для заданной высокой T и заданного p. В них при T>2500K необходимо учитывать содержание шести (k=6) вида частиц: H2O, H2, O2, H, OH, O. Уравнение имеют вид:
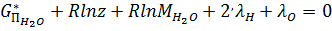 ; (18)
; (18)
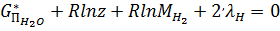 ; (19)
; (19)
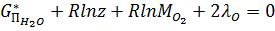 \; (20)
\; (20)
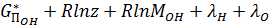 ; (21)
; (21)
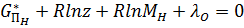 ; (22)
; (22)
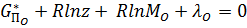 ; (23)
; (23)
-[O]+MH2O+MOH+2MH2+MH=0 (24)
-[H]+2MH2O+MOH=2MH2+MH=0 (25)
-p+zMH2O+zMH2+zMO2+zMOH+zMH+|zMO=0 (26)
Система состоит из к+m91=6+2+1=9 уравнений, которых достаточно для определения неизвестных MH2O, MH2, MO2, MOH, MH, MO, z,λH и λO, по ним определяется равновесный состав газовой фазы.
Вопросы
1. Явления, происходящие при возбуждении атомов и молекул.
2. Расчет равновесия диссоциации молекул через константу равновесия.
3. Расчет равновесия на основе минимизации ∆G°.
Литература
1. Жданов С.К., Курчаев В.А. и др. Основы физических процессов в плазме и плазменных установках. М.: МИФИ. 2000 – 328с.
2.Рыжонков Д.И. и др. Теории металлургических процессов.– М.: Металлургия, 1989, 392 с.
3. Казачков Е.А. Расчёты по теории металлургических процессов. - М.: Металлургия, 1988, 288 с.
Дата добавления: 2017-06-13; просмотров: 3704;











