О недостатках существующего метода перспективных построений 7 глава
Во-вторых, точка зрения O должна находиться посередине радиуса, которым наносится след проекционной поверхности в плане.
В соответствии с этими условиями проводим на чертеже через точки O оси X и Y —первую параллельно, вторую перпендикулярно прямой AB. Окончив эти предварительные построения, радиусом 0,5 R вычерчиваем в произвольном масштабе (лучше всего в мелком) полуокружность с центром в точке O. В точках пересеченья с осью Y эта окружность определит положение вершины и центра K проекционной поверхности, что позволяет, поставив ножку циркуля в точку K, радиусом R нанести в плане след искомой поверхности.
Проведя далее через крайние точки фасада лучи AO и BO, получим проекцию прямой AB на следе проекционной поверхности в виде отрезка ab. Для удобства дальнейшего построения вместо криволинейного участка проекционной поверхности выгоднее воспользоваться картинной плоскостью, задавшись ее необходимыми размерами в более крупном масштабе. В соответствии с этим параллельно отрезку ab (точнее, хорде, стягивающей точки a и b) проводим прямую A0 B0 — след картинной плоскости в плане.
Далее построения осуществляются на основе общих принципов теории линейной перспективы, то есть путем проекции фасада на картинную плоскость. При этом могут быть использованы различные способы, из которых как простейшие и наиболее приемлемые в данном случае могут быть рекомендованы следующие.
Прежде всего, для построения перспективы требуется провести линию горизонта FD и перенести на нее проекцию продольного размера фасада — A0 B0. В данном примере для наглядности мы воспользовались приемом перенесения заданных точек на горизонтальную прямую FD с помощью циркуля, расположив его ножку в точке D пересечения линии горизонта и следа проекционной поверхности.
Чтобы определить перспективные размеры высот hА и hB в соответствующих точках A0 и B0, можно воспользоваться наличием на чертеже точки схода F, полученной при пересечении следа картинной плоскости с осью X. При этом необходимо учесть также и то, что высота фасада в точке M0 пересечения его картинной плоскостью окажется равной своей натуральной величине H.
Эти данные и позволяют произвести необходимые построения. На линию горизонта вначале переносятся точки F и M0, затем в точке M0 располагается основание отрезка H — натуральной высоты фасада, взятой в масштабе чертежа. Через вершину отрезка H в точку схода F проводится прямая, которая при пересечении с двумя перпендикулярами, восстановленными в точках A0 и B0, определит перспективные контуры фасада здания.
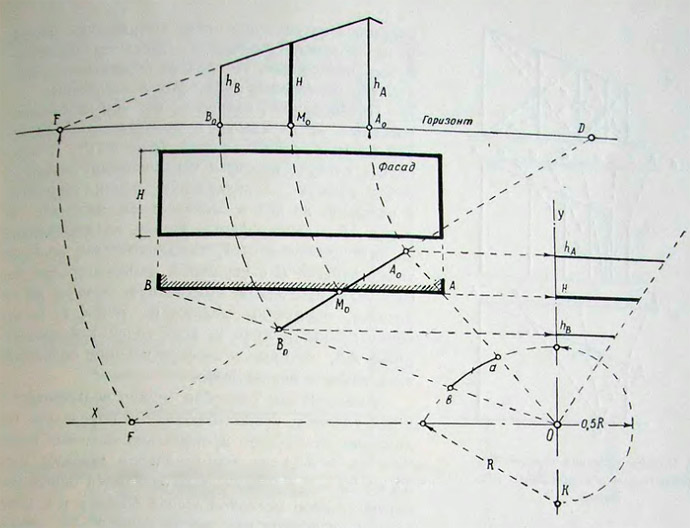
52. Пример перспективного построения плоскости фасада объекта прямоугольной формы
В тех случаях, когда воспользоваться точкой схода бывает затруднительно, например, при ее расположении за пределами чертежа, можно обратиться к другому приему построения, используя для этой цели боковую проекцию объекта и картинной плоскости.
В данном примере проекцией фасада здания будет являться отрезок H, наложенный перпендикулярно к оси Y на продолжении прямой AB . Искомые отрезки hA и hB также с проектируются в свою натуральную величину, заняв аналогичное положение между осью Y и лучом, проходящим через вершину отрезка H. Причём высоты эти окажутся расположенными на прямых, проходящих через точки A0 и B0 параллельно оси X.
Зная горизонтальную проекцию фасада AB и проекционные размеры высот hA и hB,произвести дальнейшее построение изображения уже не составляет большого труда.
Оба описанных выше способа определения перспективных размеров высот мы будем применять и в дальнейшем при построении более сложных объектов. Первый — при наличии на чертеже точки схода для группы горизонтальных прямых, второй — при ее отсутствии или же при необходимости получения большего числа проекций вертикальных размеров.
Следует сказать также о некоторых приемах перспективного подразделения плоскости фасада в продольном направлении, к которым нам придётся неоднократно обращаться при последующих построениях. Среди этих приемов следует указать, прежде всего, на простейший случай метрического членения фасада с помощью диагоналей, которые всякий раз при пересечении определяют перспективное положение центра прямоугольника, которому они соответствуют (рис. 53, а). Если же фасад расчленён на нечётное число метрических частей и использовать указанный способ не представляется возможным, то следует обратиться к приему так называемых делительных масштабов.
Предположим, например, что нам необходимо разделить фасад здания в продольном направлении на пять равных частей (рис. 53,6). В этом случае следует провести через вершину ближнего ребра прямую, параллельную линии горизонта и отложить на ней в произвольном масштабе отрезок AB — размер фасада здания, подразделенный на пять равных частей. Соединив далее крайнюю точку отрезка B с вершиной дальнего ребра фасада B0 и продолжив полученную прямую до горизонта, определим положение точки W. В эту точку проведем лучи из всех точек членения отрезка AB, которые и засекут искомое положение этих точек в перспективе.
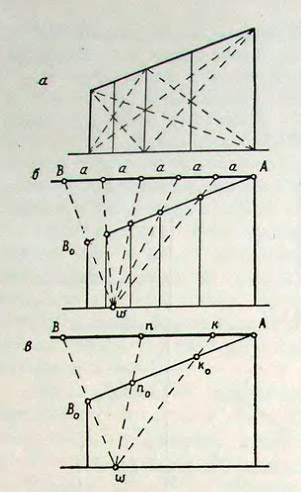
53. Приёмы членения перспективы прямоугольника в заданном отношении
Аналогичным способом можно пользоваться и в тех случаях, когда необходимо определить положение каких-либо произвольно заданных точек, представленных на ортогональном чертеже (рис. 53, в). Так, к примеру, если требуется определить перспективное местоположение точек пик, нанесенных на фасаде или же на прямой AB, равной его длине, то, как и в предыдущем примере, располагаем отрезок AB параллельно линии горизонта и проводим луч B0, определяющий положение точки W. Затем проводим из заданных точек n и k лучи в точку W, которые засекают положение этих точек на прямой AB0.
Рассмотренные выше примеры касались приемов перспективного построения плоской прямоугольной фигуры. Однако изложенные выше принципы построения распространяются и на другие случаи перспективного изображения. В частности, они имеют непосредственное отношение к построению перспективных изображений объемных фигур. Обратимся к одному из таких объектов и рассмотрим в качестве примера построение контуров здания, имеющего форму параллелепипеда. На чертеже представлены план и фасад объекта, точка зрения O, а также расположена линия горизонта на 1/4 части высоты здания, считая от основания (рис. 54).
Особенность перспективного построения параллелепипеда выражается, прежде всего, в необходимости произвести построение не одного, как в предыдущей примере, а двух фасадов здания. В соответствии с этим при построении потребуется использовать не одну, а две проекционные поверхности для каждого фасада в дельности.
Исходя из этих условий, производим следующее построение. Проводим через точку зрения O оси X и Y, располагая их параллельно сторонам плана объекта.
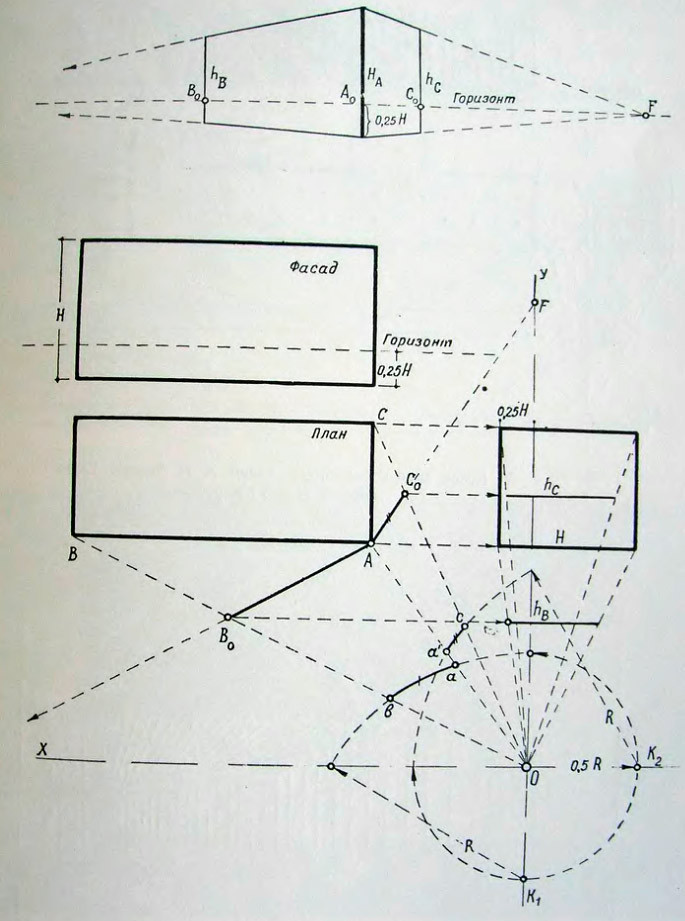
54. Примеры перспективного построения объекта прямоугольной формы
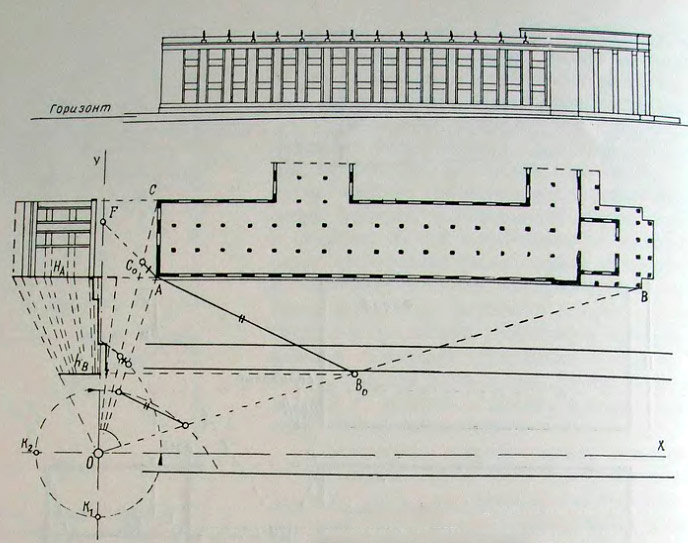
55. Новое здание библиотеки В. И. Ленина. Схема перспективного построения
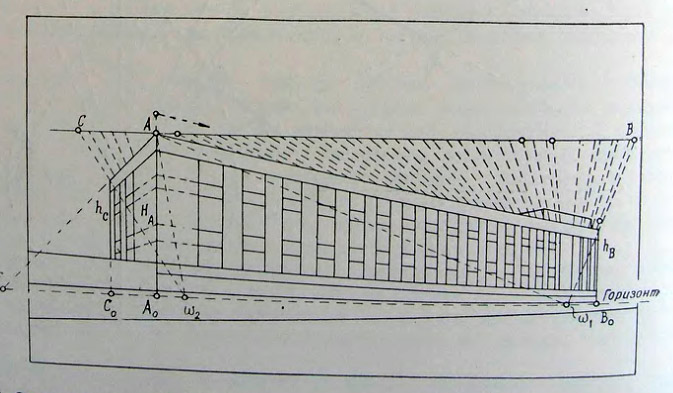
56. Схема перспективного изображения нового здания библиотеки имени В. И. Ленина

57. Перспективный вид нового здания библиотеки имени В. И. Ленина. Фотоснимок и перспектива, построенная рекомендуемым методом с той же точки зрения
Затем произвольно избранным радиусом, равным 0,5 R, из точки O вычерчиваем окружность, которая определит на осях X и Y положение центров K1 и K2 и вершины двух проекционных поверхностей. Проведя далее лучи AO, BO и CO, найдем проекции ab и a'c сторон плана на полученных поверхностях.
Расположенные изолированно, проекции эти оказываются, однако, разномасштабными, так как высота объекта H, расположенная в точке A, не получает при проекции на эти поверхности равных размеров.
Поэтому при замене этих поверхностей двумя соответственно параллельным, картинными плоскостями последние необходимо располагать таким образом, чтобы они пересекались в плане на луче, направленном к ближайшему от зрителя углу здания.
Такими плоскостями (точнее, их следами) в данном примере будут являться AB0 и AC0, точка пересечения которых в плане для удобства построения совмещена с точкой A — основанием ближнего к зрителю вертикального ребра здания.
Установив положение картинных плоскостей, переходим к построению перспективы объекта, которое осуществляется обычными приемами. Прежде всего, в верхней части рисунка проводим линию горизонта и располагаем на ней последовательно отрезки AB0, AC0 — проекции сторон плана AB и AC, а также отрезок C0F, определяющий положение точки схода F для бокового фасада параллелепипеда.
Так как ближнее к зрителю ребро фасада HA совпадает с линией пересечения картинных плоскостей, то естественно, что он получится на перспективе в натуральную величину. Поэтому, взяв отрезок HA, равный высоте фасада, располагаем его таким образом, чтобы линия горизонта проходила на высоте 0,25 H от основания ребра. Теперь, соединив концы отрезка HA с точкой F, получаем перспективный вид бокового фасада объекта, ограниченный высотами HA и hC.
Аналогичным образом можно было бы построить также перспективу второго фасада, если бы на чертеже имелась точка схода для горизонтальных прямых, параллельных оси X. Но так как эта точка находится за пределами чертежа, то для определения высоты hB следует воспользоваться боковой проекцией фасада, приняв при этом ось Y за линию горизонта. Искомый отрезок hB окажется заключенным между двумя лучами, идущими в точку O от вершин ближнего к зрителю ребра H. Место его расположения определяется при проведении через точку B0 прямой линии, параллельной оси X.
Перспективный размер отрезка hC, определенный нами ранее, может быть установлен также и описанным выше способом. Для этого необходимо провести два луча, идущих к вершине дальнего ребра бокового фасада, и затем определить величину заключенного между ними отрезка прямой, проходящей через точку параллельно оси X.
Полученные данные о перспективных размерах высот объекта позволяют завершить построение перспективы параллелепипеда.
С помощью описанных выше приемов строятся и архитектурные перспективы сооружений несложной формы. В качестве одного из подобных примеров paccмотрим перспективное построение нового здания библиотеки имени В. И. Ленина в Москве.
Выбранная для построения перспективы точка зрения расположена в плане у края тротуара на противоположной стороне Моховой улицы (рис. 55). Угол зрения в горизонтальной плоскости на объект равен 60°, а в вертикальной — около 30°. Высота расположения горизонта принята нормальной, то есть соответствующей высоте человеческого роста.
Переходя к построению, прежде всего определяем место и характер расположения двух картинных плоскостей AB0 и AC0, которые размещаем таким образом чтобы линией их пересечения служило ближнее к зрителю ребро объекта. Их расположение в плане определяем, как и в предыдущих примерах, с помощью соответствующих участков двух вспомогательных проекционных поверхностей вычерченных в мелком масштабе из центров K1 и K2.
Полученные при проекции перспективные размеры горизонтальных сторон здания AB0 и AC0 переносим с плана на перспективу, располагая их на линии горизонта (рис. 56). При этом если требуется, производим пропорциональное увеличение размеров в необходимое число раз. Затем в точке A0 перпендикулярно к горизонту размещаем натуральную высоту объекта HA с намеченными на ней делениями, соответствующими основным членениям фасада по вертикали. Через вершину отрезка HA проводим прямую в точку схода F, также перенесенную с плана. Прямая эта в пересечении с вертикалью, проведенной в точке C0, определит внешние очертания бокового фасада. Из точек деления ребра AA0 в точку F проводим также прямые, которые будут соответствовать основным горизонтальным членениям здания.
Для построения перспективы главного фасада определяем перспективные размеры дальнего ребра объекта — hB. С этой целью используем, как и в предшествующих примерах, боковой фасад объекта, расположенный на оси Y, как на линии горизонта (рис. 55). Проведя через точку B прямую, параллельную оси X, получаем на ней в створе между лучами, направленными к вершинам отрезка HA, искомую нами величину hB. Так как точка схода для горизонтальных членений главного фасада лежит далеко за пределами чертежа, то для удобства дальнейшего построения сносим с бокового фасада (с отрезка HA) на отрезок hB все точки, характеризующие расположение основных членений. Перенеся далее отрезок hB с чертежа плана на перспективу и расположив его в пункте B0 (рис. 56), соединяем его вершину и точки, отмечающие положение членений, с соответствующими точками отрезка HA.
Для завершения перспективного построения представленного объекта в общих массах требуется также расчленить его фасады в продольном направлении. Решить эту задачу можно следующим образом.
Через точку A на перспективном изображении проводим горизонтальную прямую. Затем откладываем на ней отрезки AB и AC, представляющие собой продольную и поперечную стороны плана, расчлененные на соответствующие части, соединив далее точку B с вершиной отрезка hB, а точку C с вершиной отрезка hC и продлив их до горизонта, получим точки W1 и W2. В эти последние и следует направить ряд лучей из точек, нанесенных на отрезках AB и AC. В пересечении с прямыми, проходящими через вершины отрезков HA, hB, и hC, эти лучи определят расположения вертикальных членений фасадов здания.
Полученная описанным выше путем схема может служить основой для успешного завершения перспективного построения. При этом могут быть использованы как рекомендуемые теорией линейной перспективы способы геометрического построения, так и приемы прорисовки деталей на глаз, которые при наличии известного опыта у рисующего всегда себя оправдывают на практике.
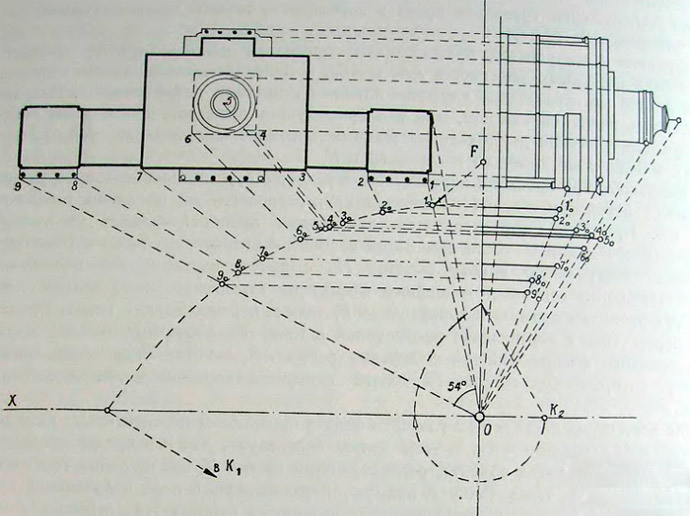
58. План и фасад дома Пашкова в Москве. Схема перспективного построения
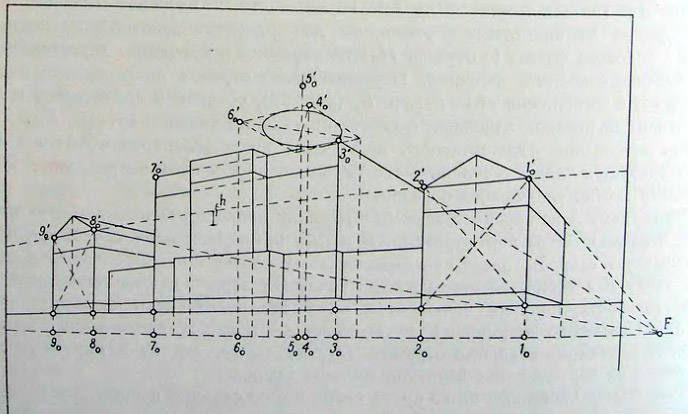
59. Схема перспективного изображения дома Пашкова

60. Сопоставление фотоснимка и перспективного изображения дома Пашкова, построенного с применением нескольких точек схода
Перспективное изображение здания библиотеки, построенное на основе данной схемы, представлено на рисунке 57. Здесь же помещена фотография здания, выполненная с той же точки зрения. На фотоснимке здание выглядит чрезмерно удлиненным. Усиленный перспективный ракурс придает ему неестественный вид. Напротив, построенное рекомендуемым методом изображение передает вид здания более правдиво, позволяя зрителю составить более правильное впечатление о его пропорциях и размерах.
В дополнение к рассмотренному случаю приведем еще один пример построения перспективы объекта более сложной конфигурации — старого здания библиотеки имени В. И. Ленина, или так называемого дома Пашкова, построенного по проекту крупнейшего русского зодчего XVIII века В. И. Баженова. Точка зрения, как и в предыдущем примере, располагается на противоположной стороне Моховой улицы (рис. 58). Угол зрения на объект в горизонтальной плоскости равен 54°, а в вертикальной — около 27°, считая от горизонта.
Характерной особенностью формы дома Пашкова является его расчлененность на несколько самостоятельных частей — центральный объем здания с фонарем, два боковых портика и две соединяющие эти объемы галереи. При восприятии здания с заданной точки наблюдения фасадные плоскости этих объемов будут видны зрителю в различной степени ракурса. Ближние в меньшем, удаленные — в более сильном сокращении.
Для наиболее точной передачи указанных перспективных явлений следует учитывать эти особенности, определяя в процессе построения перспективы степень ракурсных сокращений для каждого из соответствующих элементов здания в отдельности.
Поэтому, проведя из точки K1, след проекционной поверхности и спроектировав на него план объекта, мы заменим полученную кривую не одной, а несколькими хордами, стягивающими дуги 1020, 2030, 3070 и так далее. Здесь же, пользуясь изображением бокового фасада здания, получим проекционные величины высот боковых портиков (10', 20', 80', 90') , главного объема (30' и 70'), высоты фонаря (50') и точек описанного вокруг него квадрата, используемого для построения перспективы окружности (40', 60'). Эти точки определяют положение вершин проекций соответствующих отрезков, общая высота которых отсчитывается от горизонта, то есть от оси Y.
Полученные таким путем проекционные размеры основных горизонтальных размеров и высот здания переносим на перспективу (рис. 59), где первые (точки 10, 20, 30, и т. д.) располагаем на линии горизонта в соответствующем порядке и с необходимыми интервалами, а вторые — перспективные размеры высот — откладываем на вертикальных прямых, проходящих через соответствующие точки, от линии горизонта. Соединяя далее точки 10' и 20', 30' и 70' и т. д., а также используя точку схода F для прямых, перпендикулярных к оси X, получаем на перспективе очертания общих контуров изображаемого объекта.
Продолжая построение, находим место некоторых промежуточных членений высот, определяющих положение основания дома Пашкова над горизонтом, высоту цокольного этажа, венчающих здание антаблементов и фронтов. Эти точки вместе с дополнительными данными о проекционном расположении некоторых промежуточных вертикальных членений, например, сторон центрального портика, позволяют получить перспективное изображение объекта в общих массах, как это показано на рисунке 59.
Дальнейшее построение сводится главным образом к последовательному уточнению и деталировке полученной схемы. В законченном виде такая перспектива представлена на рисунке 60 вместе с фотоснимком, выполненным с той же точки зрения. Сравнение этих изображений показывает, что применение рекомендуемого метода приводит к устранению усиленных ракурсов и перспективных сокращений, имеющих место на фотоснимке. Искривления же горизонтальных линий, возникшие в результате фрагментарного перспективного построения объемов здания, не бросаются зрителю в глаза.
Перспектива высотного сооружения
Рассмотренные примеры перспективных построений выполнялись, как мы видели, при вертикальных углах зрения, не превышающих 30-35°, считая от горизонта. В указанных пределах перспективные сокращения по вертикали практически незаметны, и поэтому они не учитывались при построениях.
Совсем иначе обстоит дело при изображении архитектурных объектов в сильных вертикальных ракурсах, когда, например, требуется получить перспективу отдельных фрагментов высотных сооружений при обозрении снизу. Здесь учет перспективных сокращений по вертикали для достижения правдивости подобных изображений совершенно необходим. Но так как построения, производимые с помощью наклонной картинной плоскости, не всегда дают в этих случаях положительные результаты, то следует обратиться к другой системе построения, опирающейся в своих основах на практику реалистического рисунка. В качестве примера, иллюстрирующего возможности предлагаемого способа, опишем ход построения перспективы верхних ярусов колокольни Ивана Великого в Московском Кремле.
Точка зрения, выбранная для построения, удалена от основания колокольни на тридцатиметровое расстояние. При этом угол зрения на вершину креста от горизонта составляет 64° (рис. 61). Однако в перспективе должна быть изображена лишь часть здания, начиная от завершения первого яруса, обозреваемая под вертикальным углом в 38°.
Построение перспективы начинаем с размещения на фасадном чертеже следа картинной поверхности I, который представляет собою часть эллипса, вписанного в прямоугольник с отношением сторон 1:2,2. Эта кривая позволяет нам получить проекционные размеры основных вертикальных элементов здания ярусов, купола, креста. Причем главными опорными пунктами при этом должны служить точки 1, 2…7, расположенные по внешнему, обращенному к зрителю контуру сооружения. Полученные таким путем размеры, помеченные на следе проекционной поверхности цифрами 10, 20…70, переносим на осевую линию перспективного изображения, которое нам предстоит построить (рис. 62).
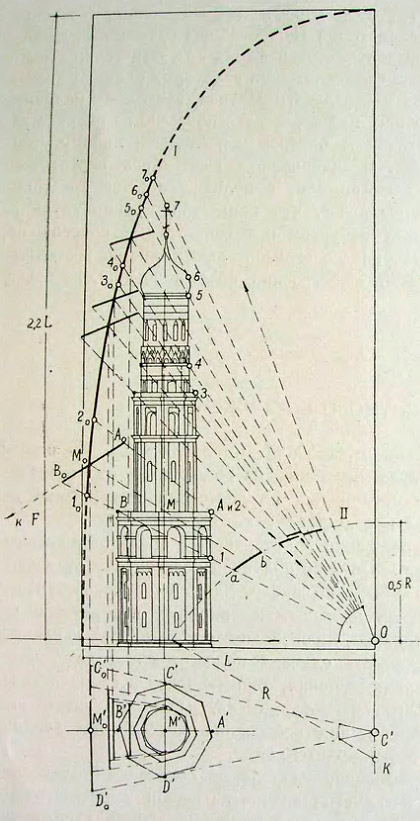
61. План и фасад колокольни Ивана Великого. Схема перспективного построения
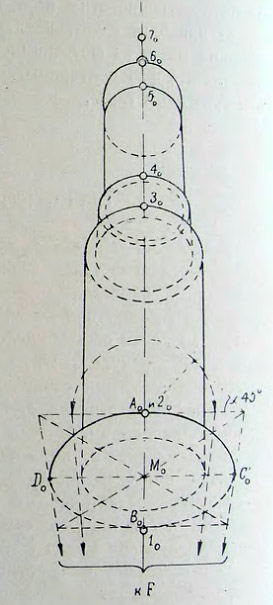
62. Схема перспективного изображения фрагмента колокольни Ивана Великого в сильном вертикальном ракурсе

63.Сопоставление фотоснимка и перспективного изображения фрагмента колокольни Ивана Великого, построенного рекомендуемым методом с той же точки зрения
Далее основная задача построения сводится к получению перспективных проекций нескольких наиболее характерных сечений ярусов сооружения. Три таких сечения расположены между соседними ярусами, а одно фиксирует пункт перехода от восьмигранной формы яруса к цилиндрической (рис. 61).
Для упрощения построения представим себе восьмигранные сечения соответствующих ярусов вписанными в круги. Чтобы найти правильные, неискаженные проекции этих фигур, установленную ранее проекционную поверхность использовать, однако, уже нельзя, так как с ее помощью можно определять лишь сокращения
вертикально расположенных элементов. Поэтому из произвольно заданного центра K на оси Y радиусом, равным 2OK, проведем новую вспомогательную поверхность II, на которую и спроектируем горизонтальные сечения всех ярусов. Для того однако, чтобы проекции сечений по своим размерам соответствовали установлений ранее сокращениям вертикальных элементов, их следует, пропорционально увеличив расположить вдоль следа первой проекционной поверхности, как это показано на чертеже.
Путь построения проекции каждого сечения в отдельности можно проиллюстрировать на примере одного из сечений, например AB. Прежде всего, на кривую I проектируется центр сечения — точка M. Затем через полученную точку M0, проводится прямая AB параллельно соответствующему участку ab проекционной поверхности II. Отрезок A0B0 и будет служить малой вертикальной осью эллипса, представляющего проекцию окружности, охватывающей сечение AB. Размер горизонтальной оси эллипса устанавливается путем проекции диаметра окружности C0'D0' на отрезок C0'D0', лежащий на вертикальной прямой, проходящей через точку M0.
Имея эти данные, откладываем вниз от точки 20 на перспективной схеме (рис. 62) отрезок A0B0, совмещая точки A0 и 20. При этом одновременно получаем положение перспективного центра — точку М0, позволяющего разместить горизонтальную ось эллипса C0'D0', размеры которой берем с плана. Если полученных четырех точек и положения перспективного центра эллипса оказывается недостаточно для проведения кривой, то тогда следует обратиться к рекомендуемым в подобных случаях приемам вписывания эллипса в перспективу квадрата. При этом, однако, следует помнить, что точка схода для боковых сторон такого квадрата будет находиться ниже линии горизонта. Ее точное местоположение может быть установлено при продолжении отрезка A0B0 до пересечения линии горизонта в точке F (рис. 61) и при последующем переносе отрезка A0F на перспективу. Последний откладывается по оси вниз от точки 20.
Описанным выше способом строятся также перспективы остальных окружностей, расположенных в заданных сечениях. Проведенные к полученным эллипсам касательные определят общие контуры объемов башни, как это видно на представленном чертеже (рис. 62). Дальнейшее построение сводится к вписыванию в цилиндры восьмигранных призм, к размещению промежуточных членений ярусов и к прорисовке деталей. Перспективное изображение ярусов башни в законченном виде представлено на рисунке 63. Рядом с этим изображением помещен фотоснимок, выполненный с той же точки зрения, что и осуществленное нами построение. Хотя здесь главная точка картины расположена в центре представленного кадра, завершение башни имеет ярко выраженную перспективно утрированную форму. Сооружение кажется нам непомерно вытянутым вверх.
Рассмотренный пример дает лишь общую принципиальную схему построения перспективы высотного сооружения. Эта схема на практике может несколько видоизменяться в зависимости от формы объекта, величины угла зрения и т. д. В частности для упрощения построений отдельные участки криволинейной проекционной поверхности могут заменяться плоской картиной, а при значительных вертикальных углах может быть использована так же точка схода для вертикалей.
При построении перспективы ансамбля необходимо стремиться не только к правильности перспективного изображения отдельных объектов, но также соблюдать верность объемно-пространственной передачи соотношений, определяющих целостное впечатление зрителя о пропорциях, размерах и расположении окружающих сооружений.
Предположим, что необходимо построить перспективу площади, окруженной с трех сторон застройкой равной высоты (рис. 64). Причем часть площади ABCD, попадающая в поле зрения, представляет собой в плане прямоугольник правильной формы.
Прежде всего, требуется установить, в каком перспективном сокращении будут находиться ближние к зрителю высоты боковой застройки, помещенные в точках A и D, а также соответствующее расстояние между ними. Для этого необходимо использовать проекционную поверхность, вершина которой и центр K1, располагаются на оси Y, перпендикулярной к прямой AD. Кривизна следа этой поверхности несколько больше обычной, так как точка зрения O находится не посередине радиуса, а делит его в отношении 2:3 (2/5R и 3/5R).
Проекции hA и hD указанных высот HA и HD получаем на разрезе в верхней части чертежа. Установив проекционную высоту ближних к зрителю частей застройки, приступаем к определению перспективных размеров высот дальнего плана HB и HC, размещенных в точках B и C. С этой целью вычерчиваем след проекционной поверхности, обращенной своей вершиной к прямой AB, то есть к линии боковой застройки, находящейся в меньшем ракурсе. Как и у первой кривой, точка O делит здесь радиус в отношении 2:3. Проведя далее отрезок A0B0 параллельно участку a'b' вычерченной кривой, получаем проекционную
поверхность для определения перспективных высот боковой застройки левой стороны площади. При этом на вертикальной прямой, проходящей через точку B0, находим на разрезе искомую высоту hB.

64. Схема перспективного построения застройки площади прямоугольной формы без применения точек схода
Для определения перспективных размеров застройки фронтальной стороны площади BC может быть использован участок bc первой проекционной поверхности, предназначенной для проекции прямых, параллельных оси X. Однако месторасположение хорды bc должно быть изменено. Она должна занять положение отрезка B0C0, что обеспечит проекционное соответствие размеров высот сторон AB и BC.
Дата добавления: 2017-06-13; просмотров: 1455;











