Примеры решения задач
Задача 1. Пусть X=[0,1[´[0,1[, S – полукольцо прямоугольников, принадлежащих 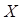 , вида Tab=[a,b[´[0,1[. Положим m(Tab) = b–a. Найти внешнюю меру множества
, вида Tab=[a,b[´[0,1[. Положим m(Tab) = b–a. Найти внешнюю меру множества 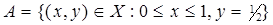 и выяснить, является ли оно измеримым. Описать явный вид лебеговского продолжения меры.
и выяснить, является ли оно измеримым. Описать явный вид лебеговского продолжения меры.
Решение.По определению внешняя мера А
m*(A)= 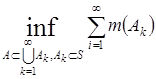 , где любой элемент полукольца S имеет вид
, где любой элемент полукольца S имеет вид 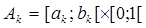 , т.е. полностью определяется своей проекцией на ось OX. Чтобы покрыть множество А элементами
, т.е. полностью определяется своей проекцией на ось OX. Чтобы покрыть множество А элементами 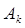 , необходимо и достаточно покрыть проекцию этого множества на ось OX полуинтервалами
, необходимо и достаточно покрыть проекцию этого множества на ось OX полуинтервалами 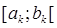 . Поэтому внешняя мера множества А в данном случае совпадает с внешней мерой проекции этого множества на ось OX.
. Поэтому внешняя мера множества А в данном случае совпадает с внешней мерой проекции этого множества на ось OX.
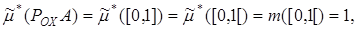
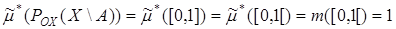 ,
,
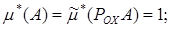
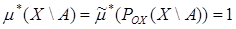 ;
;
и 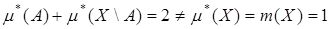 .
.
Следовательно, множество А неизмеримо. Из приведенных выше рассуждений видно, что множество 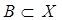 будет измеримым тогда и только тогда, когда оно будет иметь вид b ´ [0,1[ и b Ì [0,1[ – измеримо по Лебегу.
будет измеримым тогда и только тогда, когда оно будет иметь вид b ´ [0,1[ и b Ì [0,1[ – измеримо по Лебегу.
Задача 2. Пусть X= [0,1[´[0,1[, S={[a,b[´[c,d[ÌX}, m([a,b[´[c,d[) = = (b-a)(d-c). Вычислить внутреннюю и внешнюю меры множества 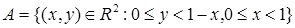 .
.
Решение.По определению
m*(A)= 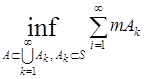 , A
, A 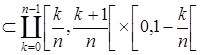 , т.е. прямоугольники,
, т.е. прямоугольники, 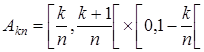 , где k=0, 1, 2,¼, n-1, образуют для каждого n покрытие множества А. Имеем:
, где k=0, 1, 2,¼, n-1, образуют для каждого n покрытие множества А. Имеем:
m*(A)£ 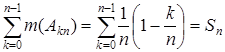 .
.
Величина Sn является верхней суммой Дарбу для функции f(x)=1–x на отрезке 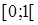 ,соответствующей разбиению отрезка на n частей. Для функции f существует интеграл Римана, поэтому
,соответствующей разбиению отрезка на n частей. Для функции f существует интеграл Римана, поэтому
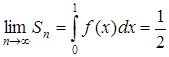 .
.
Переходя к пределу при n®¥ в неравенстве m*A £ Sn, которое выполняется для всех n, получим m*A£1/2. С другой стороны m*(X\A)£ 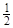 , т. к. X \ A Ì
, т. к. X \ A Ì 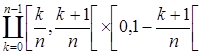 , и m*(X \ A) £
, и m*(X \ A) £ 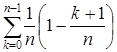 .
.
Поэтому m* A = mX–m* (X \ A) ³ 1–1/2 = 1/2. Имеем:
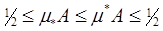 .
.
Задача 3. Пусть 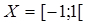 ,
, 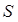 – полукольцо,
– полукольцо, 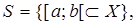 F:X®R – неубывающая непрерывная слева на Х функция. Определим на
F:X®R – неубывающая непрерывная слева на Х функция. Определим на 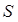 меру Лебега-Стилтьеса равенством:
меру Лебега-Стилтьеса равенством: 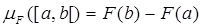 .
.
Описать класс измеримых подмножеств из Х, найти меру Лебега-Стилтьеса каждого множества А, если
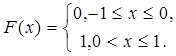
Решение.Из определения меры mF на полукольце S следует, что 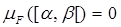 , если полуинтервал не содержит точку x = 0, и
, если полуинтервал не содержит точку x = 0, и 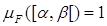 , если
, если 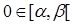 . Распространим меру mF на минимальное кольцо K(S). Если A Î K(S), то
. Распространим меру mF на минимальное кольцо K(S). Если A Î K(S), то 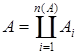 , Ai = [ai,bi[. Поэтому если 0
, Ai = [ai,bi[. Поэтому если 0 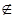 A, то 0
A, то 0 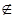 [ai,bi[ для всех i =
[ai,bi[ для всех i = 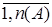 и
и 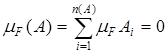 . Если
. Если 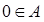 , то найдётся только один полуинтервал
, то найдётся только один полуинтервал 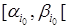 , содержащий x = 0, с мерой 1, и
, содержащий x = 0, с мерой 1, и 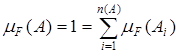 . Следовательно, мера каждого элемента кольца равна либо 0, либо 1. Поскольку F(x) непрерывна слева, то mF s-аддитивна и допускает продолжение.
. Следовательно, мера каждого элемента кольца равна либо 0, либо 1. Поскольку F(x) непрерывна слева, то mF s-аддитивна и допускает продолжение.
С этой целью найдём вначале внешнюю меру множества 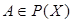 . По определению
. По определению
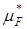 (A)=
(A)= 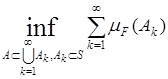 ,
,
где нижняя грань берётся по всем конечным или счётным покрытиям множества 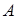 элементами
элементами 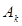 полукольца
полукольца 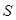 .
.
Если 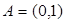 , то, рассматривая покрытия (0,1) =
, то, рассматривая покрытия (0,1) = 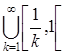 , имеем
, имеем 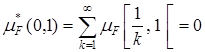 . Поскольку m*A ³ m*A, то
. Поскольку m*A ³ m*A, то 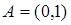 измеримо относительно меры mF и его мера равна нулю. В силу полноты меры будет измеримым и любое подмножество интервала (0,1) и его мера будет также равна нулю.
измеримо относительно меры mF и его мера равна нулю. В силу полноты меры будет измеримым и любое подмножество интервала (0,1) и его мера будет также равна нулю.
Если рассмотреть одноточечное множество 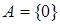 , то для каждого его покрытия
, то для каждого его покрытия 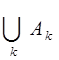 множествами
множествами 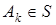 имеется хотя бы одно из них, содержащее точку x = 0. Поэтому
имеется хотя бы одно из них, содержащее точку x = 0. Поэтому 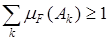 и
и 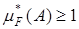 . Далее, пользуясь покрытием [-1,1[ É {0}, получаем, что
. Далее, пользуясь покрытием [-1,1[ É {0}, получаем, что 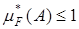 . Таким образом,
. Таким образом, 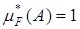 .
.
Рассмотрим теперь произвольное множество 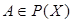 . Из свойств монотонности внешней меры следует, что
. Из свойств монотонности внешней меры следует, что 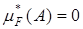 , если A Ì (0,1) или A Ì [-1,0). Если же {0} Ì A, то
, если A Ì (0,1) или A Ì [-1,0). Если же {0} Ì A, то 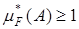 . Рассматривая в этом случае покрытие [-1,1[, имеем
. Рассматривая в этом случае покрытие [-1,1[, имеем 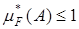 . Следовательно, если {0} Ì A, то
. Следовательно, если {0} Ì A, то 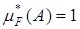 .
.
Покажем теперь, что произвольное множество измеримо относительно меры Лебега-Стилтьеса. Действительно, A Ì (0,1) или AÌ [-1,0), то 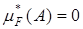 и оно измеримо. Если же {0} Ì A, то из неравенства
и оно измеримо. Если же {0} Ì A, то из неравенства 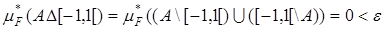 , справед-ливого для каждого e > 0, заключаем, что множество А mF-измеримо,
, справед-ливого для каждого e > 0, заключаем, что множество А mF-измеримо, 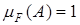 .
.
Задача 4. Пусть X = R2, S = {Dkn=[k, k+1[´[n, n+1[: k, n Î Z}, m(Dkn)=1. Найти внешнюю меру множества
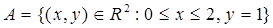 .
.
Будет ли множество А измеримым?
Решение.Множество Х является пространством с s-конечной мерой, т.к. X= 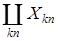 ,
, 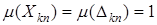 , здесь
, здесь 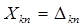 .
.
По определению множество А измеримо, если измеримо A1=A 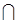 D11, A2 = A
D11, A2 = A 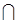 D21, A3 = A
D21, A3 = A 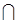 D31, тогда A1 = {0 £ x < 1, y = 1}; A2={1£ x < 2, y = 1}; A3 = {x = 2, y = 1}.
D31, тогда A1 = {0 £ x < 1, y = 1}; A2={1£ x < 2, y = 1}; A3 = {x = 2, y = 1}.
По определению m*(A1) = 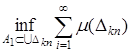 , тогда
, тогда 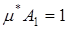 , т.к. покрытие, на котором достигается точная нижняя грань, образует множество D11,
, т.к. покрытие, на котором достигается точная нижняя грань, образует множество D11, 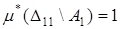 ,
, 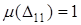 . Поэтому A1, и, следовательно, A не измеримо. Очевидно, что m*(A)= 3, т.к. покрытие A состоит из D11, D21, D31.
. Поэтому A1, и, следовательно, A не измеримо. Очевидно, что m*(A)= 3, т.к. покрытие A состоит из D11, D21, D31.
Задача 5. Каково строение и какая мера точек отрезка [0,1], десятичное представление которых возможно без цифр 4 и 5.
Решение.Это множество строится следующим образом: делим отрезок [0,1] на десять равных частей и выбрасываем полуинтервал [0.4, 0.6]. Затем каждый из оставшихся восьми полуинтервалов делим на десять равных частей и выбрасываем в каждом из них соответствующий полуинтервал [0,n14; 0,n16[, где n1 = 0,1,2,3,6,7,8,9 и т.д. Данное множество нигде не плотно, каждая его точка является предельной, т.е. множество является совершенным. Вычислим меру выбрасываемых промежутков, посчитав тем самым меру дополнения к искомому множеству:
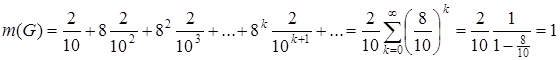 .
.
Следовательно, мера точек отрезка [0,1], десятичное представление которых возможно без цифр 4 и 5, равна 0.
Задача 6. Найти меру множеств
1) 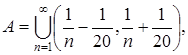 2)
2) 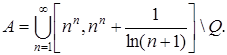
Решение.1) Представим множество А в виде объединения попарно непересекающихся интервалов. Для этого выясним, начиная с какого номера n интервалы будут пересекаться. Заметим, что 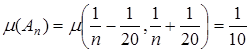 для всех n, и поэтому интервалы не могут быть вложены друг в друга. Решая неравенство
для всех n, и поэтому интервалы не могут быть вложены друг в друга. Решая неравенство 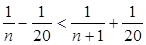 , находим n ³ 3. Поэтому представим А в виде
, находим n ³ 3. Поэтому представим А в виде 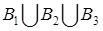 , где
, где 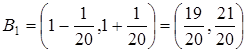 ,
,
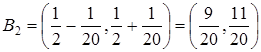 ,
, 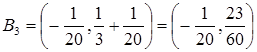 , тогда
, тогда 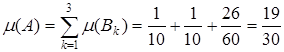 .
.
2) Пусть 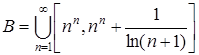 .
.
Множество В борелево и поэтому измеримо. Множество Q счётное и имеет меру нуль, значит 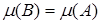 . Множества
. Множества 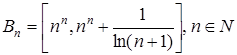 – непересекающиеся при любом
– непересекающиеся при любом 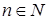 .
.
Согласно свойству s-аддитивности меры: 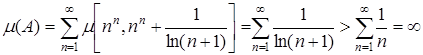 . Таким образом,
. Таким образом, 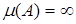 .
.
Задача 7. Вычислить меру множества А:
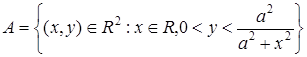 ,
,
где a > 0 – фиксированное число.
Решение.Множество A Ì R2 открыто и поэтому измеримо. Множество А рассматривается в пространстве с s-конечной мерой, поэтому построим возрастающую последовательность множеств 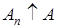
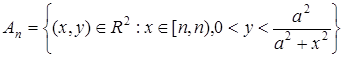 .
.
Тогда 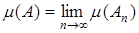 .
.
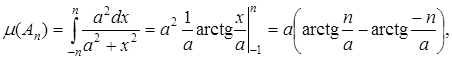
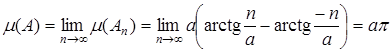 .
.
Задание 1. Пусть 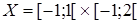 ,
, 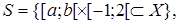
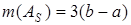 . Найти внешнюю и внутреннюю меры множеств и выяснить, измеримы ли они.
. Найти внешнюю и внутреннюю меры множеств и выяснить, измеримы ли они.
1.1. 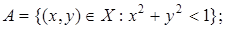
1.2. 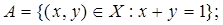
1.3. 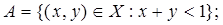
1.4. 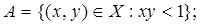
1.5. 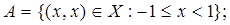
1.6. 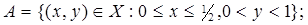
1.7. 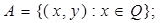
1.8. 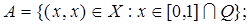
1.9. 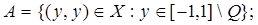
1.10. 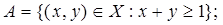
1.11. 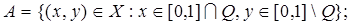
1.12. 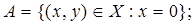
1.13. 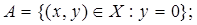
1.14. 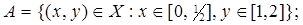
Задание 2. Пусть X =[-2,2[, 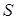 ={[a,b[ÌX},
={[a,b[ÌX}, 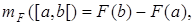
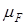 – её продолжение по Лебегу.
– её продолжение по Лебегу.
а) Найти меру множества, состоящего из одной точки.
б) Выяснить, является ли множество А измеримым, найти его меру.
2.1. 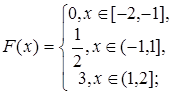
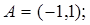
2.2. 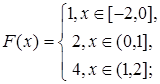
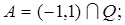
2.3. 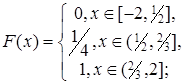
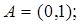
2.4. 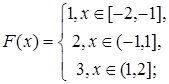
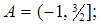
2.5. 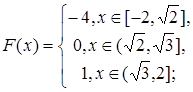 A=[0,3/4];
A=[0,3/4];
2.6. 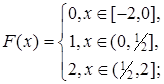
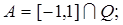
2.7. 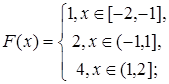
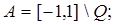
2.8. 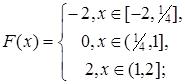
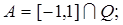
2.9. 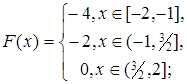
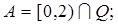
2.10. 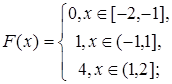
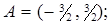
2.11. 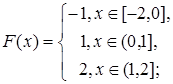
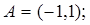
2.12. 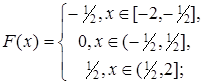
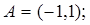
2.13. 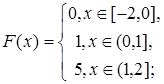
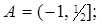
2.14. 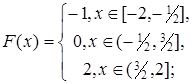 A=[-1,2);
A=[-1,2);
Задание 3. Описать структуру множества A Ì [0,1] и найти его меру.
3.1. Множество точек отрезка [0,1], состоящее из чисел, у которых в десятичной записи цифра 2 встречается раньше, чем цифра 3.
3.2. Множество точек отрезка [0,1], в разложении которых в бесконечную десятичную дробь фигурируют все цифры 1,2,…9.
3.3. Множество точек отрезка [0,1], десятичное представление которых содержит хотя бы одну цифру 3.
3.4. Множество точек отрезка [0,1], десятичное представление которых возможно без цифр 4 и 5.
3.5. Множество точек отрезка [0,1], которые допускают десятичное разложение без комбинации стоящих рядом цифр 3,3,3.
3.6. Множество точек отрезка [0,1], которые допускают разложение в десятичную дробь без использования цифры 7.
3.7. Множество точек отрезка [0,1], десятичное представление которых не содержит цифры 2.
3.8. Множество точек отрезка [0,1], десятичное представление которых содержит цифру 5 только один раз.
3.9. Множество точек отрезка [0,1], в разложении которых в двоичную дробь на всех чётных местах стоят нули.
3.10. Множество точек отрезка [0,1], в разложении которых в двоичную дробь на всех нечётных местах стоят единицы.
3.11. Множество точек отрезка [0,1], троичное представление которых не содержит цифры 3.
3.12. Множество точек отрезка [0,1], троичное представление которых не содержит цифры 0.
3.13. Множество точек отрезка [0,1], десятичное представление которых невозможно без цифры 4.
3.14. Множество точек отрезка [0,1], которые допускают десятичное разложение без комбинации стоящих рядом цифр 2,2,2,2.
Задание 4. Доказать, что множество 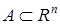 измеримо и найти его меру.
измеримо и найти его меру.
4.1. Множество точек единичного квадрата на плоскости, состоящее из точек, декартовы и полярные координаты которых иррациональны.
4.2. 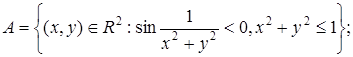
4.3. Множество точек единичного квадрата на плоскости, состоящее из точек 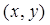 таких, что
таких, что 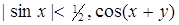 - иррационально.
- иррационально.
4.4. 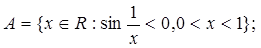
4.5. 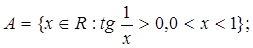
4.6. Множество точек единичного квадрата на плоскости, состоящее из точек 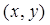 таких, что
таких, что 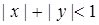 .
.
4.7. 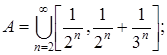
4.8. 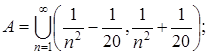
4.9. 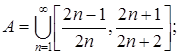
4.10. Множество точек единичного квадрата на плоскости, состоящее из точек 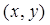 таких, что
таких, что 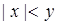 .
.
4.11. Множество точек единичного квадрата на плоскости, состоящее из точек 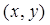 таких, что
таких, что 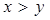 .
.
4.12. 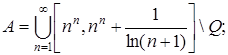
4.13. 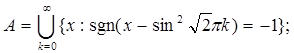
4.14. 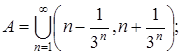
| <== предыдущая лекция | | | следующая лекция ==> |
| Пусть Z – множество целых чисел. Задает ли данная формула меру на Р (Z) | | | Сходимость по мере. |
Дата добавления: 2021-07-22; просмотров: 472;










