Логарифмические частотные характеристики

Частотные характеристики достаточно сложно строить вручную. В 60-е годы, когда развивалась классическая теория управления, не было мощных компьютеров, поэтому наибольшую популярность приобрели приближенные методы, с помощью которых можно было проектировать регуляторы с помощью ручных вычислений и построений. Один из таких подходов основа на использовании логарифмических частотных характеристик.

Вместо A(ω) было предложено использовать логарифмическую амплитудную частотных характеристику (ЛАЧХ): график, на котором по оси абсцисс откладывается десятичный логарифм частоты (lgω), а по оси ординат – величина L_m(ω)=20lgA(ω), измеряемая в децибелах (дБ). При построении логарифмической фазовой частотной характеристики (ЛФЧХ) по оси абсцисс также откладывается логарифм частоты lgω.

Единицей отсчета на логарифмической оси частот является декада – диапазон, на котором частота увеличивается в 10 раз (а значение ее логарифма увеличивается на единицу). Вместе ЛАЧХ и ЛФЧХ называются логарифмической амплитудно-фазовой частотной характеристикой (ЛАФЧХ) или диаграммой Боде.

Логарифмические характеристики обладают двумя ценными свойствами

1) ЛАЧХ и ЛФЧХ для произведения W₁(s)·W₂(s) вычисляются как суммы ЛАЧХ и ЛФЧХ отдельных звеньев

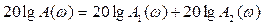, (24)

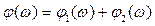. (25)

2) в области высоких и низких частот ЛАЧХ асимптотически приближаются к прямым, наклон которых составляет ± 20 дБ/дек (децибел на декаду), ± 40 дБ/дек и т.д.

В классической теории управления хорошо разработаны методы анализа и синтеза систем на основе асимптотических ЛАЧХ, которые представляют собой ломаные линии и легко строятся вручную. C появлением компьютерных средств расчета практическая ценность ЛАФЧХ несколько снизилась, однако они по сей день остаются простейшим инструментом прикидочных расчетов для инженера.

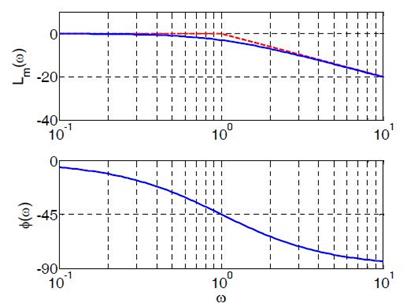
На рисунке показаны точная (сплошная синяя линия) и асимптотическая (штриховая красная линия) ЛАФЧХ для звена первого порядка с передаточной функцией

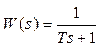при Т = 1с.

Первая асимптота, определяющая поведение ЛАЧХ на низких частотах, имеет нулевой наклон, потому что звено относится к классу позиционных звеньев, имеющих постоянный ненулевой статический коэффициент усиления, то есть

.

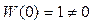Если W(0) = 0, передаточная функция содержит множитель s^k(k > 0), который соответствует производной порядка k. В этом случае наклон ЛАЧХ на низких частотах равен k⋅20 дБ/дек.

Если W(0) = ∞, звено содержит один или несколько интеграторов, то есть в знаменателе есть сомножитель s^k. Тогда наклон ЛАЧХ на низких частотах равен − k⋅20 дБ/дек.

Наклон ЛАЧХ на высоких частотахопределяется разностью степеней числителя и знаменателя передаточной функции. Если числитель имеет степень m, а знаменатель – степень n, то наклон последней асимптоты равен 20⋅(m − n) дБ/дек. В нашем примере m − n = 0 − 1 = −1. Поэтому вторая асимптота, определяющая свойства звена на высоких частотах, имеет наклон −20 дБ/дек, то есть, за одну декаду значение уменьшается на 20 дБ.