Дросселирование газов и паров
Дросселирование – это эффект падения давления при преодолении потоком рабочего тела сопротивления, например: частично открытого вентиля, задвижки, шибера, пористой стенки (рис. 6.9).
 Данный процесс является необратимым адиабатным (dq = 0, dsH > 0), в котором полезная работа не совершается, а изменение кинетической энергии пренебрежимо мало.
Данный процесс является необратимым адиабатным (dq = 0, dsH > 0), в котором полезная работа не совершается, а изменение кинетической энергии пренебрежимо мало.
Согласно уравнения первого закона термодинамики (6.2) при 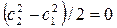 : h1 = h2, т.е. энтальпия рабочего тела в процессе дросселирования не изменяется.
: h1 = h2, т.е. энтальпия рабочего тела в процессе дросселирования не изменяется.
Таким образом, при дросселировании рабочего тела:
· давление уменьшается (dp < 0);
· энтальпия не изменяется (dh = 0);
· энтропия увеличивается (ds > 0);
· удельный объем увеличивается (dv > 0).
При дросселировании идеального газа температура не изменяется
(dT = 0), т.к. h = f(T).
При дросселировании реальных газов и паров температура может увеличиваться, уменьшаться или не изменяться для одного и того же рабочего тела. Это зависит от параметров, при которых газ либо пар дросселируются.
Изменение температуры реальных газов и паров характеризуется дифференциальным эффектом дросселирования:  .
.
При ah > 0 – температура уменьшается (dT < 0).
При ah < 0 – температура увеличивается (dT > 0).
При ah = 0 – температура не изменяется (dT = 0).
Состояние рабочего тела, в котором ah = 0, называется точкой инверсии, а соответствующая ей температура – температурой инверсии (Tинв). При атмосферном давлении для: водорода - tинв = -57 0С, гелия - tинв = -239 0С, водяного пара - tинв = 4097 0С. При температурах t < tинв температура рабочего тела в процессе дросселирования уменьшается.
 На рис. 6.10 показан процесс дросселирования перегретого пара в h-s- диаграмме, его температура уменьшается (t2 < t1).
На рис. 6.10 показан процесс дросселирования перегретого пара в h-s- диаграмме, его температура уменьшается (t2 < t1).
Дросселирование является необратимым процессом, протекающим с увеличением энтропии и с потерей эксергии, которые можно рассчитать по формулам DsH==s2-s1 и (6.35).
Адиабатное дросселирование используется в технике для получения низких температур и сжижения газов. В измерительной технике процессы дросселирования лежат в основе методов определения расхода жидкости или газа, степени сухости паров. Этот эффект иногда используется для уменьшения мощности тепловых двигателей.
 На рис. 6.11 показан обратимый адиабатный процесс расширения рабочего пара от p1 до p2 в паровой турбине.
На рис. 6.11 показан обратимый адиабатный процесс расширения рабочего пара от p1 до p2 в паровой турбине.
Работа данного процесса равна l = h1 – h2.
После дросселирования пара в задвижке до давления p1д работа обратимого адиабатного процесса расширения уменьшилась 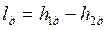 , следовательно, уменьшилась мощность турбины.
, следовательно, уменьшилась мощность турбины.
6.10. Методические указания и вопросы
1. Уясните физический смысл отдельных членов уравнения первого закона термодинамики для потока, поймите разницу между внешней и технической работой, и в каком случае они тождественны.
2. Каково назначение сопел и диффузоров? Как влияет профиль канала на скорость адиабатного потока? Как изменяются параметры в зависимости от изменения скорости (dc>0, dc<0)? Как выбрать форму сопла в каждом конкретном случае?
Уясните, что в суживающихся и цилиндрических каналах скорость потока не может превысить скорость звука.
3. Расчет истечения выполняется на основе модели адиабатного процесса газа или пара со всеми вытекающими отсюда особенностями расчета газов и паров.
При вычислении скорости (c, м/с), подкоренное выражение в формулах должно иметь размерность Дж/кг, т.к. Дж/кг = м2/с2.
4. Уясните особенности истечения с учетом трения: определение параметров действительного процесса, скорости и характерных сечений сопла, расчет потерь кинетической энергии и эксергии.
5. Как изменяются параметры газов и паров при дросселировании? Можно ли этот процесс считать предельным случаем необратимого адиабатного истечения рабочего тела из сопла? Каково практическое применение процессов дросселирования?
Задачи
1. Рассчитайте параметры торможения p0, t0, v0 потока воздуха, имевшего скорость 500 м/с при p =1 бар, t = 30 0С.
2. Определите параметры торможения (h0, p0) потока сухого насыщенного пара, движущегося со скоростью c = 300 м/с при p =10 бар.
3. Параметры воздуха на входе в сопло равны: p1 = 20 бар, t1 = 300 0С, скорость c1= 0, давление среды pc = 1 бар.
Рассчитайте скорость (c2) и скорость звука (a2) на выходе из: а) сопла Лаваля; б) суживающегося сопла.
Решение
Рассчитывается 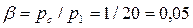 и сравнивается с bkp. Для воздуха (табл. 6.1) bkp = 0,528, следовательно, в нашем случае b <bkp.
и сравнивается с bkp. Для воздуха (табл. 6.1) bkp = 0,528, следовательно, в нашем случае b <bkp.
При установке сопла Лаваля давление на выходе из сопла p2 = pc, скорость сверхзвуковая (c2 > a2) рассчитывается по формуле (6.19)
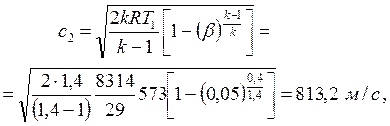 
|
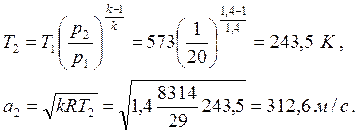 
|
В варианте установки суживающегося сопла при b < bkp давление на выходе из сопла p2 = pkp, скорость равна скорости звука (c2 = ckp = a2), по формуле (6.22) имеем
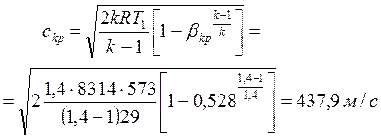 . . 
|
Ответ: а) c2 = 813,2 м/с, a2 = 312,6 м/с; б) c2 = a2 = 437,9 м/с.
4. Водяной пар под давлением p1 = 10 бар и при температуре t1 = 320 0С, истекая из сопла Лаваля, расширяется адиабатно до давления p2 = 1 бар.
Определить площадь выходного и минимального сечений сопла, если массовый расход пара равен G = 4 кг/с.
Решение
Выходное и минимальное сечения рассчитываются по уравнениям неразрывности потока (6.31), (6.33):
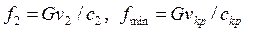 , , 
|
скорости - по формулам:
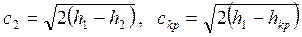 . . 
|
Для перегретого пара из табл. 6.1 выбираем bkp = 0,546. Давление пара в минимальном сечении сопла:
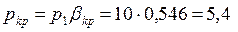 бар. бар. 
|
Из h-s- диаграммы для адиабатного процесса расширения находятся необходимые параметры: h1 = 3140 кДж/кг, hkp = 2950 кДж/кг, h2 = 2620 кДж/кг, vkp = 0,44 м3/кг, v2 = 1,7 м3/кг.
Тогда
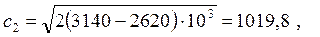 м/с м/с 
|
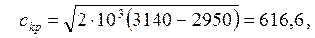 м/с
м/с
f2 = 4.1,7/1019,8 = 6,67.10-3 м2,
fmin =4. 0,44/616,6 =2,85.10-3 м2
Ответ: f2 = 6,67.10-3 м2 , fmin = 2,85.10-3 м2.
5. При выпуске из баллона азот дросселируется от исходного состояния, характеризуемого параметрами: p1 = 20 МПа, t1 = 20 0С, до давления
p2 = 8 МПа.
Определить плотность азота после дросселирования а также изменение энтропии в процессе дросселирования, считая азот идеальным газом, имеющим постоянную теплоемкость.
6. Как изменится температура при дросселировании сухого насыщенного водяного пара с давлением p1= 20 бар до p2 = 1 бар ?
Ответы
1.t0 = 155 0С, p0 = 1,104 бар, v0 =1,111 м3/кг. 2.h0= 2822 кДж/кг,
p0 = 12,5 бар.5. r = 91,95 кг/м3, Ds = 0,272 кДж/(кг.К).
6.Dt=t1 - t2 = 52 0С.
ВЛАЖНЫЙ ВОЗДУХ
Влажный воздух – это смесь сухого воздуха и водяного пара.
Давление влажного воздуха равно сумме парциальных давлений сухого воздуха (pс.в.) и водяного пара (pп)
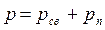 . . 
| (7.1) |
Поскольку pп << pсв, то сухой воздух, водяной пар, а также их смесь (влажный воздух) можно считать идеальными газами.
Пар, содержащийся во влажном воздухе с температурой T, может быть перегретым (точка B, рис. 7.1). В этом случае pп < ps при данной T.
 Влажный воздух, содержащий перегретый пар, называется ненасыщенным (pп < ps).
Влажный воздух, содержащий перегретый пар, называется ненасыщенным (pп < ps).
Если pп = ps при данной температуре воздуха (точка A, рис. 7.1), то пар является сухим насыщенным. Влажный воздух, содержащий сухой насыщенный пар, называется насыщенным (pп = ps).
Ненасыщенный влажный воздух можно перевести в состояние насыщения двумя способами:
1. Увеличивая давление pп до ps при данной температуре влажного воздуха T (процесс B - A, рис. 7.1), например, увеличивая количество пара в воздухе за счет испарения воды.
2. Снижая температуру влажного воздуха при pп = const (процесс В - Г ).
Температура, при которой давление пара (pп) становится равным давлению насыщения (ps), называется температурой точки росы (Tp), и она измеряется гигрометром.
Если охлаждать насыщенный влажный воздух (процесс А - Г), то из него будет выпадать влага, т.к. уменьшается давление насыщения (psГ < psA).
Дата добавления: 2021-07-22; просмотров: 1002;











