Препроцессинг в современных программных системах решения задач дискретной оптимизации.
Современные программные пакеты широко используют средства препроцессинга (предварительной обработки) данных модели. Препроцессинг ‑ фаза между формулированием модели и ее решением, которая применяет простые логические правила (тесты) для переформулировки задачи и сжатия линейной релаксации. При этом препроцессинг может также уменьшить размер задачи в результате фиксирования некоторых переменных и исключения ряда ограничений, а также выявить недопустимость задачи.
Простейшее логическое тестирование основано на границах переменных и правых частей ограничений. Пусть 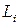 ‑ любая нижняя граница значения
‑ любая нижняя граница значения 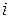 -й строки
-й строки 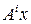 при ограничении
при ограничении 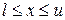 , и пусть
, и пусть 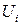 ‑ любая верхняя граница значения
‑ любая верхняя граница значения 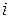 -й строки
-й строки 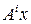 при ограничении
при ограничении 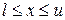 . Ограничение
. Ограничение 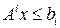 избыточно, если
избыточно, если 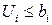 и недопустимо, если
и недопустимо, если 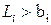 . Граница переменной может быть уточнена на основе информации о том, что ограничение становится недопустимым при присвоении переменной значения этой границы.
. Граница переменной может быть уточнена на основе информации о том, что ограничение становится недопустимым при присвоении переменной значения этой границы.
7.2. Приближенные алгоритмы.
7.2.1. Метод вектора спада для приближенного решения задач дискретной оптимизации.
Рассмотрим из приближенных методов ‑ метод вектора спада, разработанный И. В. Сергиенко в середине 60-х годов прошлого века. В общем случае этот метод позволяет находить локальный минимум целевой функции задачи ДО, однако, если она имеет соответствующие свойства выпуклости, то он приводит к определению глобального минимума.
Рассмотрим задачу ЦЛП вида:
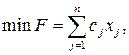 (7.9)
(7.9)
при ограничениях:
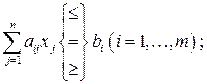 (7.10)
(7.10)
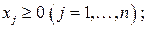 (7.11)
(7.11)
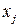 — целые
— целые 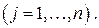 (7.12)
(7.12)
Введем необходимые понятия. Пусть М ‑ некоторое дискретное точечное пространство. 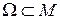 ‑ множество допустимых решений задачи ЦЛП (7.9) - (7.12). Введем метрику
‑ множество допустимых решений задачи ЦЛП (7.9) - (7.12). Введем метрику 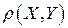 в пространстве М, т.е. функцию, которая определяет расстояние между произвольными точками этого пространства Х и Y. Метрика должна удовлетворять трем аксиомам:
в пространстве М, т.е. функцию, которая определяет расстояние между произвольными точками этого пространства Х и Y. Метрика должна удовлетворять трем аксиомам:
1) аксиоме тождества: 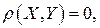 при условии, что X = Y;
при условии, что X = Y;
2) аксиоме симметрии: 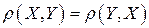 ;
;
3) аксиоме неравенства треугольника 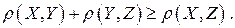
Метрику 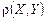 можно определять по-разному. В частности, в прямоугольной декартовой системе координат это может быть
можно определять по-разному. В частности, в прямоугольной декартовой системе координат это может быть 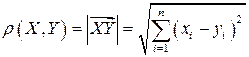 , где
, где 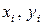 - соответственно координаты точек X и Y в пространстве М.
- соответственно координаты точек X и Y в пространстве М.
Пусть 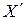 ‑ некоторое допустимое решение задачи ЦЛП. Для некоторого числа
‑ некоторое допустимое решение задачи ЦЛП. Для некоторого числа 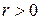 множество всех точек, для которых выполняется неравенство
множество всех точек, для которых выполняется неравенство 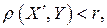 называется открытой окрестностью с центром в точке
называется открытой окрестностью с центром в точке 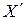 и радиусом r, а множество всех точек
и радиусом r, а множество всех точек 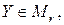 для которых выполняется неравенство
для которых выполняется неравенство 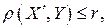 называется замкнутой окрестностью.
называется замкнутой окрестностью.
Определим некоторое окрестность 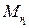 точки
точки 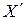 с радиусом r1 такую, чтобы кроме решения, она содержала бы и другие решения задачи, для чего радиус r1 должен быть не меньше некоторой величины R. Далее будем рассматривать только указанные окрестности решений задачи. Определим функцию
с радиусом r1 такую, чтобы кроме решения, она содержала бы и другие решения задачи, для чего радиус r1 должен быть не меньше некоторой величины R. Далее будем рассматривать только указанные окрестности решений задачи. Определим функцию 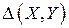 следующим образом:
следующим образом: 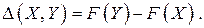
Назовем вектором спада 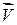 функции
функции 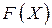 в некоторой окрестности точки
в некоторой окрестности точки 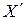 , являющейся одним из допустимых решений
, являющейся одним из допустимых решений 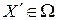 задачи ЦЛП, вектор, компонентами которого являются величины
задачи ЦЛП, вектор, компонентами которого являются величины 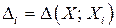 , где
, где 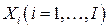 - решения задачи, принадлежащих окрестности
- решения задачи, принадлежащих окрестности 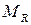 .
.
При неотрицательности всех компонент вектора спада 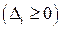 в окрестности точки
в окрестности точки 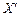 получим для любого значения
получим для любого значения 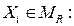
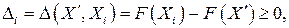
т.е. точка 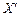 является точкой локального минимума функции
является точкой локального минимума функции 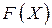 в выделенной окрестности
в выделенной окрестности 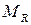 , то есть:
, то есть:
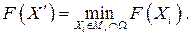
Если некоторые компоненты вектора спада отрицательны, это означает, что 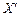 не является точкой минимума в указанной окрестности, поскольку в некоторых точках этой окрестности функция
не является точкой минимума в указанной окрестности, поскольку в некоторых точках этой окрестности функция 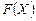 приобретает меньшие значения. Причем та точка
приобретает меньшие значения. Причем та точка 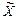 рассматриваемой окрестности, для которой разность
рассматриваемой окрестности, для которой разность 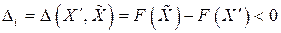 минимальна, определяет направление наискорейшего уменьшения целевой функции
минимальна, определяет направление наискорейшего уменьшения целевой функции 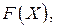 так как
так как
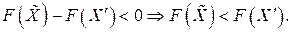
Это свойство и лежит в основе вычислительной схемы метода вектора спада. Идея метода заключается в определении компонент вектора спада для некоторой начальной точки. Если все они неотрицательны, то точка локального минимума найдена, иначе находим центр новой окрестности и проверяем его компоненты на неотрицательность. Процесс поиска решения является последовательным перебором точек, уменьшающих значение целевой функции.
Как правило, на каждом шаге алгоритма (т.е. для каждой новой окрестности) не нужно вычислять все компоненты вектора спада, а лишь часть из них, что дает существенный выигрыш в объеме и продолжительности вычислений.
Приведем один из возможных алгоритмов реализации метода вектора спада.
1. Выбрать начальную точку Х0 и радиус окрестности R так, чтобы точка Х0 была допустимым решением задачи ЦЛП 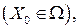 а окрестность содержала также другие допустимые решения задачи. Этот выбор может осуществляться случайно с проверкой выполнения указанных условий.
а окрестность содержала также другие допустимые решения задачи. Этот выбор может осуществляться случайно с проверкой выполнения указанных условий.
2. Определяются компоненты вектора спада в выбранном окрестности. Если все его компоненты неотрицательны, то локальный минимум найден (т.е. задача решена и оптимальным целочисленным решением является 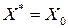 ).
).
3. Если не все компоненты вектора спада неотрицательны, то выбираем наименьшую компоненту 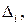 которая и определяет точку
которая и определяет точку 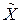 с меньшим значением целевой функции и центром новой окрестности.
с меньшим значением целевой функции и центром новой окрестности.
4. Возвращаемся к пункту 2. Процесс продолжаем, пока для некоторого 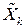 все компоненты соответствующего вектора спада не будут неотрицательными.
все компоненты соответствующего вектора спада не будут неотрицательными.
Пример. Решим задачу целочисленной оптимизации
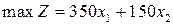 ,
,
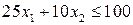 ;
;
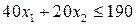 ;
;
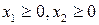 ,
,
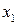 и
и 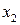 — целые.
— целые.
Решение. Пусть 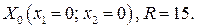 Выбранная точка является допустимым решением задачи, поскольку удовлетворяет всем ограничениям и условию целочисленности, а окрестность выбранного радиуса содержит другие решения задачи, например, точку
Выбранная точка является допустимым решением задачи, поскольку удовлетворяет всем ограничениям и условию целочисленности, а окрестность выбранного радиуса содержит другие решения задачи, например, точку 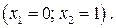
Определяем точки, принадлежащие рассматриваемом окрестности (рис. 7.1). Это такие три точки: 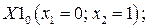
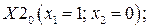
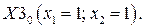
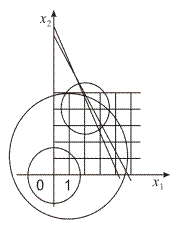
Рис. 7.1. Окрестность.
Определим компоненты вектора спада:
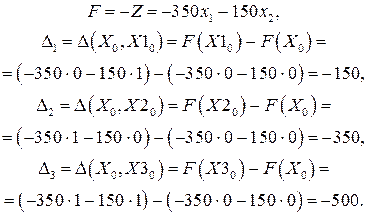
Наименьшей является третья компонента вектора спада, следовательно, соответствующая ей точка становится центром следующей окрестности 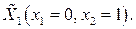 . Радиус
. Радиус 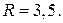
В новую окрестность будут входить точки с координатами:
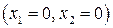
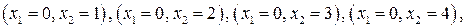
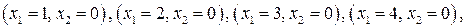
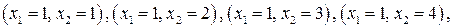
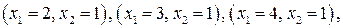
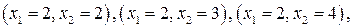
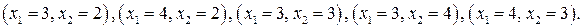
Необходимо вычислить значения компонент вектора спада для указанных точек. Однако для трех точек нужные величины были рассчитаны на предыдущем шаге, и остается вычислить компоненты вектора для новых точек.
После проведения вычислений получаем, что наименьшее значение приобретает компонента вектора, которая соответствует точке 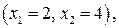 поэтому следующий центр окрестности перемещается в новую точку
поэтому следующий центр окрестности перемещается в новую точку 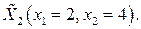 . Пусть
. Пусть 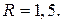
Вычисляем компоненты вектора спада лишь в двух точках окрестности:

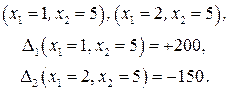
Сравнивая эти значения, определяем точку нового центра окрестности 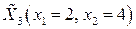 с радиусом
с радиусом 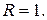 Компоненты вектора спада в этом окрестности приобретают только положительные значения. Следовательно, процедура приближения завершена, и эта точка является оптимальным решением целочисленной задачи:
Компоненты вектора спада в этом окрестности приобретают только положительные значения. Следовательно, процедура приближения завершена, и эта точка является оптимальным решением целочисленной задачи: 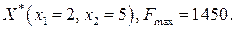
Дата добавления: 2016-06-05; просмотров: 1539;










