Метод ветвлений и отсечений.

Методыотсечения и методы ветвлений и отсечений

Методы отсечения.

Методы отсечения опираются на следующее утверждение: если ослабление задачи ЦЛП имеет нецелочисленное оптимальное решение 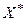, то существует неравенство

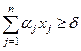, (7.2)

которому 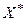не удовлетворяет, а любое допустимое решение исходной задачи ЦЛП удовлетворяет. Неравенство (7.2) называют правильным отсечением.

Методы отсечения также вкладываются в схему Джеффриона и Марстена, описанную в главе 6. Запишем первый алгоритм Р. Гомори.

Шаги 1,2 — стандартные.

Шаг 3. Формальный (список всегда из одной задачи).

Шаг 4. Релаксация всех условий целочисленности.

Шаг 5. Решение с помощью алгоритма линейного программирования (двойственный симплекс-метод).

Шаг 6. Стандартный.

Шаг 7. Пропускается.

Шаг 8. Стандартный.

Шаг 9. Всегда переход к шагу 10.

Шаг 10. «Сжатие» текущей релаксации путем добавления отсечения.

Шаг 11. Никогда не имеет места.

Шаг 12. Стандартный.

Опишем подробнее основанный на симплексном методе метод отсечения Гомори, который использует довольно простой метод построения правильного отсечения для решения полностью целочисленных задач. Если задача ослабления ЦЛП имеет оптимальный план 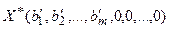, то мы можем выразить 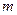базисных переменных задачи через 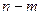небазисных переменных.

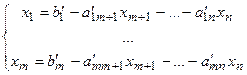, (7.3)

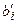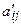где и - преобразованные значения свободных членов и коэффициентов при неизвестных системы ограничений, взятые из последней итерации симплексной таблицы. Если некоторая 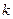-я переменная опорного плана 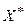принимает дробное значение 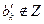, то можно показать, что ограничение

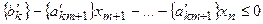, (7.4)

полученное из 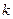- го уравнения системы (7.4), обладает всеми свойствами правильного отсечения. Символ {} в (7.4) означает дробную часть[1] соответствующего числа.

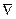Обозначим через 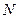совокупность небазисных переменных и на основании последней итерации симплексной таблицы запишем разложение базисной переменной 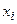по небазисным переменным .

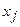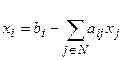. (7.5)

Теорема 7.1. Пусть 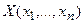- допустимое решение задачи ЦЛП. Тогда отсечение, сформулированное по правилу

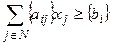(7.6)

является правильным. Докажем, что значение 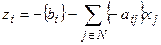является целым числом. Перепишем (7.5) в виде:

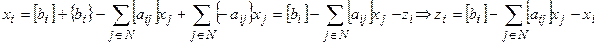На основании предположений о допустимости решения 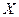- 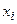и 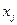являются целыми. Остальные части последнего выражения – целые по определению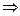 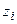- целое.

Докажем, что 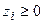. Допустим от противного, что 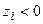. Тогда:

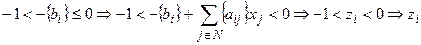- не целое. Полученное противоречие свидетельствует о ложности утверждения 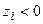. Следовательно, при любом допустимом 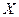выполняется неравенство .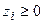

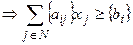Докажем, что любое оптимальное решение релаксации задачи ЦЛП, не являющееся решением ЦЛП – не удовлетворяет правильному отсечению (7.6). Пусть в оптимальном решении релаксации 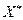значение 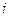- й базисной переменной – дробное. Поскольку решение 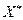оптимально, то все небазисные переменные равны нулю. Учитывая это: 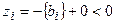, что свидетельствует о невыполнимости условия правильного отсечения .

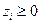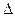
Первый этап метода Гомори состоит в определении симплексным методом оптимального решения задачи ЛП – релаксации задачи ЦЛП. После того, как это решение найдено, анализируются его компоненты. Если среди компонент нет дробных чисел, то найденное решение является оптимальным решением задачи ЦЛП. Если же некоторая переменная 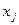принимает дробное значение, и в j-м ограничении есть дробные коэффициенты, то к системе ограничений добавляют правильное отсечение (дополнительное ограничение Гомори):

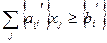, (7.7)

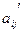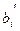где и - коэффициенты при неизвестных и свободные члены системы ограничений, взятые из строки, соответствующей переменной 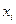, в последней итерации симплекс-таблицы.

Если в оптимальном решении задачи ЛП дробные значения принимают несколько переменных, то дополнительное неравенство составляется для переменной с максимальной дробной частью. Полученная задача ЛП решается либо двойственным симплексным методом, либо методом искусственного базиса.

Метод ветвлений и отсечений.

Выполняющимся неравенством (valid inequality) для задачи СЦЛП называется неравенство, которое выполняется для всех допустимых решений. Здесь рассмотрим выполняющиеся неравенства, которые не выполняются для всех допустимых решений линейной релаксации. Такие выполняющиеся неравенства называются отсечениями. Отсечение, которое не выполняется для данного оптимального решения линейной релаксации, называется нарушающимся отсечением.

Метод ветвлений и отсечений (branch-and-cut) является обобщением метода ветвей и границ и чистого метода отсечений Гомори, при этом после решения линейной релаксации и невозможности успешного зондирования на основе реше­ния соответствующей задачи ЛП, делается попытка нахождения нарушаю­щегося отсечения. Если найдены нару­шаю­щиеся отсечения, они добав­ляются к форму­лировке релаксационной задачи и полученная задача ЛП решается вновь. Если же нарушающегося отсечения не было найдено, производится ветвле­ние. Метод ветвлений и отсече­ний объединяет вычис­ли­тельные возможности алгоритмов ветвей и границ с теоретическими резуль­татами комбинаторики многогранников. Главными составными частями метода являются препроцессинг, решение линейных релаксаций, метод ветвей и границ, построение отсечений и эвристики.

Рассмотрим задачу ЦЛП

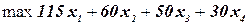
при ограничениях

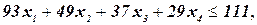
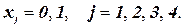
Оптимальное решение линейной релаксации имеет вид .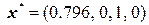

Поскольку из 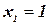следует, что все остальные переменные должны быть равны 0, а когда 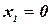, самое большее две другие переменные могут быть равны 1, ограничение

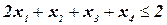
является выполняющимся неравенством.

Более того, это ограничение является нарушающимся отсечением, т.к. оно не выполняется для 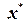. Добавляя это ограничение к линейной релаксации, мы уточним (сузим) границу, получаемую с помощью ЛП. Для данного решения линейной релаксации задачи СЦЛП, не удовлетворяющего условиям целочисленности, задача разбиения состоит в поиске нарушающегося отсечения. Можно показать, что такое отсечение существует. Именно, нарушающееся отсечение должно быть среди конечного числа линейных неравенств, определяющих множество всех выпуклых комбинаций допустимых решений. В общем случае для задач СЦЛП и ЦЛП эти неравенства, определяющие грани, очень сложно найти. Кроме того, возможно найти компромисс между «силой» отсечений и временем для их построения. Так как в случае, когда отсечение не может быть найдено за разумное время, можно начать ветвление, причем процедуры разбиения, обычно использующие быстрые эвристики, могут не найти отсечение какого-то типа, даже если эти отсечения существуют.

Алгоритм ветвлений и отсечений.

0. Инициализация. Для данной задачи ДО (P) значение целевой функции рекорда 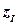находится с помощью какой-либо эвристики (если же допустимое решение задачи (P) не может быть найдено, нужно положить 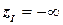). Внести в список задач-кандидатов задачу (P): .

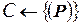1. Оптимальность. Есл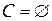и и 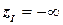, то задача (P) недопустима, конец вычислений. Есл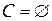и и 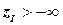, то рекорд является оптимальным решением задачи (P), конец вычислений.

2. Выбор. Используя одно из правил выбора задач-кандидатов, выбрать и удалить задачу (P) из списка .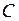

3. Граница. Решить линейную релаксацию (P_R) задачи (P). Если (P_R) недопустима – вернуться к шагу 1. В противном случае, 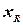‑ опимальное решение (P_R). Решить задачу разбиения для нахождения выполняющихся неравенств, нарушаемых 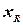. Если ни одного из выполняющихся неравенств не найдено, перейти к 4, иначе добавить выполняющиеся неравенства к описанию задачи (P) и перейти к шагу 3.

4. Зондирование. Если 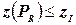, вернуться к шагу 1. Иначе, если 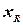допустимо для задачи (P) и 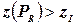, положить 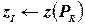, обновить рекорд (положив его равным 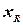) и вернуться к шагу 1. Если 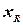допустимо для задачи (P), но 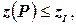вернуться к шагу 1.

5. Разбиение. Используя правила разбиения или ветвления, разбить (P) на 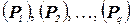, положить 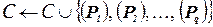и вернуться к шагу 1.