Определение ширины подошвы ленточного фундамента

Для ленточного фундамента необходимо подобрать только один размер подошвы – его ширину. Определение ширины подошвы ленточного фундамента осуществляется, как и для отдельного фундамента, последовательными приближениями.

Вначале по таблице 42 или 43 определяют расчетное сопротивление грунта R₀ для того слоя грунта, на который опирается фундамент.

Затем вычисляются ориентировочные размер ширины подошвы фундамента, как центрально загруженного, по формуле

,

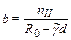(69)

где b – ширина подошвы фундамента, м;

n_II – сумма вертикальных нагрузок на одном метре длины фундамента, действующих на основание, кроме веса фундамента и грунта на его уступах (обрезах), и определяемых для случая расчета основания по деформациям, кН;

R₀, 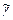– см. пояснение к формуле (58).

По полученному размеру ширины подбирают типовую фундаментную плиту и конструируют, в первом приближении, тело фундамента в соответствии с указаниями п. 5.6. После этого, согласно принятым размерам, определяют расчетное сопротивление грунта R по формуле (15), и вычисляют среднее давление по подошве фундамента по выражению

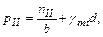
(70)

где b – ширина фундаментной плиты, м

g_mt – средневзвешенное значение удельных весов тела фундамента, грунта и пола, расположенных над подошвой фундамента; принимают равным 20 кН/м³;

d – глубина заложения фундамента, м.

Далее проверяются выполнение условия (55) и ограничений, изложенных в п. 7.2. При этом формулы для вычисления краевых давлений р_II, кПа, принимают вид:

при относительном эксцентриситете е / b £ 1/6

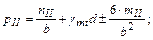
(71)

при относительном эксцентриситете е / b > 1/6

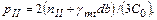
(72)

где m_II - момент от всех нагрузок, действующий по подошве на одном метре длины фундамента, найденный с учетом заглубления фундамента в грунте и перераспределяющего влияния верхних конструкций или без этого учета, кН·м;

C₀ - расстояние от точки приложения равнодействующей до края фундамента по его оси, м, определяемое по формуле

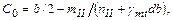
(73)

e - эксцентриситет равнодействующей нагрузки по подошве фундамента, м, определяемый по формуле

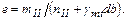
(74)