Гидростатическое давление

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рисунок 2.1, а). На дно резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G. Если эту силу P разделить на площадь дна S_abcd, то мы получим среднее гидростатическое давление, действующее на дно резервуара:

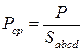(2.1)

Гидростатическое давление обладает следующими свойствами:

Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.

Для доказательства этого утверждения вернемся к рисунку 2.1, а. Выделим на боковой стенке резервуара площадку S_бок (заштриховано). Гидростатическое давление действует на эту площадку в виде распределенной силы, которую можно заменить одной равнодействующей, которую обозначим P. Предположим, что равнодействующая гидростатического давления P, действующая на эту площадку, приложена в точке А и направлена к ней под углом φ (на рисунок 2.1 обозначена штриховым отрезком со стрелкой). Тогда сила реакции стенки R на жидкость будет иметь ту же самую величину, но противоположное направление (сплошной отрезок со стрелкой). Указанный вектор R можно разложить на два составляющих вектора: нормальный R_n (перпендикулярный к заштрихованной площадке) и касательный R_τ к стенке.

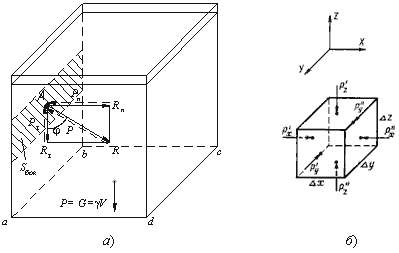
Рисунок 2.1 – Схема, иллюстрирующая свойства гидростатического давления а - первое свойство; б - второе свойство

Сила нормального давления R_n вызывает в жидкости напряжения сжатия. Этим напряжениям жидкость легко противостоит. Сила R_τ действующая на жидкость вдоль стенки, должна была бы вызвать в жидкости касательные напряжения вдоль стенки и частицы должны были бы перемещаться вниз. Но так как жидкость в резервуаре находится в состоянии покоя, то составляющая R_τ отсутствует. Отсюда можно сделать вывод первого свойства гидростатического давления.

Свойство 2. Гидростатическое давление неизменно во всех направлениях.

В жидкости, заполняющей какой-то резервуар, выделим элементарный кубик с очень малыми сторонами Δx, Δy, Δz (рисунок 2.1, б). На каждую из боковых поверхностей будет давить сила гидростатического давления, равная произведению соответствующего давления P_x, P_y , P_z на элементарные площади. Обозначим вектора давлений, действующие в положительном направлении (согласно указанным координатам) как P'_x, P'_y, P'_z, а вектора давлений, действующие в обратном направлении соответственно P''_x, P''_y, P''_z. Поскольку кубик находится в равновесии, то можно записать равенства

P'_xΔyΔz=P''_xΔyΔz
P'_yΔxΔz = P''_yΔxΔz
P'_zΔxΔy + γΔx, Δy, Δz = P''_zΔxΔy

где γ - удельный вес жидкости;
Δx, Δy, Δz - объем кубика.

Сократив полученные равенства, найдем, что

P'_x = P''_x; P'_y = P''_y; P'_z + γΔz = P''_z

Членом третьего уравнения γΔz, как бесконечно малым по сравнению с P'_z и P''_z, можно пренебречь и тогда окончательно

P'_x = P''_x; P'_y = P''_y; P'_z=P''_z

Вследствие того, что кубик не деформируется (не вытягивается вдоль одной из осей), надо полагать, что давления по различным осям одинаковы, т.е.

P'_x = P''_x = P'_y = P''_y = P'_z=P''_z

Это доказывает второй свойство гидростатического давления.

Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. Третье свойство гидростатического давления может быть записано в виде

P=f(x, y, z)