Комбинаторные аукционы
У аукциониста имеется множество объектов 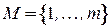 , выставленных на аукцион, а покупатели дают заявки, составляющие множество
, выставленных на аукцион, а покупатели дают заявки, составляющие множество 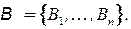 Заявка имеет вид
Заявка имеет вид 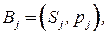 где
где 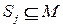 ‑ множество запрашиваемых объектов, а
‑ множество запрашиваемых объектов, а 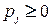 ‑ предлагаемая цена. Задача определения победителя аукциона состоит в помечивании заявок как выигравших или проигравших, максимизирующем сумму цен принятых заявок при ограничении, что каждый объект ставится в соответствие не более, чем одной заявке. Комбинаторный аукцион – частный случай рассмотренной выше задачи об упаковке.
‑ предлагаемая цена. Задача определения победителя аукциона состоит в помечивании заявок как выигравших или проигравших, максимизирующем сумму цен принятых заявок при ограничении, что каждый объект ставится в соответствие не более, чем одной заявке. Комбинаторный аукцион – частный случай рассмотренной выше задачи об упаковке.
Сформулируем модель в виде задачи ДО с бинарными переменными:
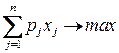
при ограничениях
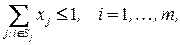
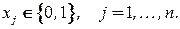
Задача о ранце
Задача о ранце является одной из известных задач исследования операций. Турист собирает в рюкзак (ранец) необходимые ему для похода вещи. У него есть 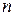 нужных ему различных предметов. Каждый предмет
нужных ему различных предметов. Каждый предмет 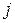 характеризуется целочисленным весом
характеризуется целочисленным весом 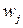 и ценностью
и ценностью 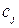 . Общий вес всех предметов больше, чем величина
. Общий вес всех предметов больше, чем величина 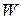 (грузоподъемность туриста). Цель состоит в выборе предметов для упаковки в рюкзак с максимальной общей ценностью при условии удовлетворения ограничения по грузоподъемности. Эта задача называется бинарной задачей о ранце, т.к. при построении ее модели используются бинарные (т.е. принимающие значения 0, 1) решающие переменные
(грузоподъемность туриста). Цель состоит в выборе предметов для упаковки в рюкзак с максимальной общей ценностью при условии удовлетворения ограничения по грузоподъемности. Эта задача называется бинарной задачей о ранце, т.к. при построении ее модели используются бинарные (т.е. принимающие значения 0, 1) решающие переменные 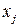 , причем
, причем 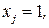 если предмет
если предмет 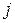 отобран для упаковки и
отобран для упаковки и 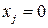 ‑ если нет. По сути, задача о ранце ‑ пример задачи о распределении ресурсов. Математическая модель имеет вид:
‑ если нет. По сути, задача о ранце ‑ пример задачи о распределении ресурсов. Математическая модель имеет вид:
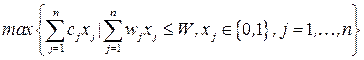 .
.
Задача о ранце может быть использована для распределения бюджетных средств 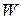 на финансирование проектов, причем проект
на финансирование проектов, причем проект 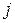 характеризуется стоимостью
характеризуется стоимостью 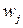 и ценностью
и ценностью 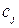
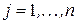 ). Задача состоит в отборе подмножества финансируемых проектов с целью максимизации их общей ценности при условии удовлетворения ограничения по выделенному бюджету.
). Задача состоит в отборе подмножества финансируемых проектов с целью максимизации их общей ценности при условии удовлетворения ограничения по выделенному бюджету.
Задачи размещения
Имеется множество 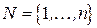 возможных мест размещения средств обслуживания клиентов и множество клиентов
возможных мест размещения средств обслуживания клиентов и множество клиентов 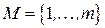 . Затраты на размещение средства обслуживания в месте
. Затраты на размещение средства обслуживания в месте 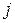 составляют
составляют 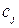 (
( 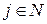 ). Каждый клиент характеризуется спросом на услуги средства обслуживания, причем полная стоимость удовлетворения спроса клиента
). Каждый клиент характеризуется спросом на услуги средства обслуживания, причем полная стоимость удовлетворения спроса клиента 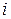 с помощью средства обслуживания, размещенного в
с помощью средства обслуживания, размещенного в 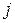 , равна
, равна 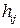 . Задача ДО состоит в выборе мест размещения средств обслуживания и последующем назначении клиентов этим средствам обслуживания, минимизирующем общую стоимость.
. Задача ДО состоит в выборе мест размещения средств обслуживания и последующем назначении клиентов этим средствам обслуживания, минимизирующем общую стоимость.
Введем бинарные переменные 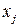 :
:
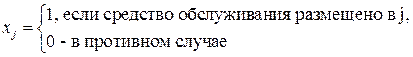
и непрерывные переменные 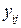 , где
, где 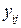 ‑ доля спроса клиента
‑ доля спроса клиента 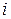 , которая удовлетворяется средством обслуживания, размещенным в
, которая удовлетворяется средством обслуживания, размещенным в 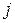 .
.
Задача размещения с неограниченной пропускной способностью имеет вид задачи ДО:
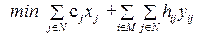
при ограничениях
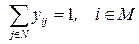
(спрос клиента 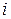 должен быть удовлетворен)
должен быть удовлетворен)
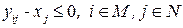
(клиент 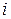 может обслуживаться средством обслуживания, размещенным в
может обслуживаться средством обслуживания, размещенным в 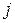 .)
.)
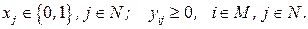
В задаче размещения с ограниченной пропускной способностью предполагается, что средство обслуживания, размещенное в 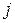 , имеет пропускную способность
, имеет пропускную способность 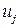 , а клиент
, а клиент 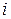 имеет спрос
имеет спрос 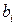 ;
; 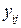 ‑ количество услуг, которые клиент
‑ количество услуг, которые клиент 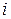 получает от средства обслуживания
получает от средства обслуживания 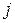 ;
; 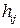 ‑ удельная стоимость услуг.
‑ удельная стоимость услуг.
Модель представляет собой следующую задачу ДО:
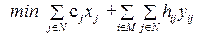
при ограничениях
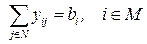
(спрос клиента должен быть удовлетворен),
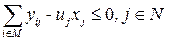
(клиенты могут обслуживаться средством обслуживания, размещенным в 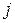 ),
),
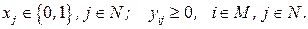
Дата добавления: 2016-06-05; просмотров: 1637;











