Каковы общие принципы усиления несущих конструкций?
При всем разнообразии приемов усиления все они базируются на двух принципах — уменьшении усилий (изгибающих моментов, продольных и поперечных сил) в конструкции или увеличении ее несущей способности. В первом случае конструкцию разгружают (т. е. передают всю или часть нагрузки на другую — усиливающую — конструкцию). Разгружение зачастую осуществляют за счет изменения расчетной схемы существующей конструкции (например, превращают балку из однопролетной в двухпролетную, подводя под нее дополнительную опору). Во втором случае увеличивают (наращивают) сечение конструкции или увеличивают сопротивление материала (например, за счет поперечного обжатия). Конечно, такое разделение достаточно условно — часто в одном приеме усиления используют оба принципа.
6.2. Что значит "включить" в работу усиливающую конструкцию?
После завершения строительно-монтажных операций по усилению усиливающая конструкция должна сразу же, как только начала прикладываться дополнительная нагрузка, воспринимать причитающуюся ей часть этой нагрузки (усилий, напряжений), т. е. деформироваться совместно с усиливаемой конструкцией, — это и называется включением ее в работу. В противном случае разрушение усиливаемой конструкции может произойти раньше, чем усиливающая начнет воспринимать свою долю нагрузки.
Например, если под железобетонную балку в середине пролета подвести дополнительную жесткую опору в виде стойки и оставить между ними зазор, то балка при увеличении нагрузки будет в состоянии прогибаться (а значит, в ней будет расти и изгибающий момент) до тех пор, пока зазор не исчезнет (рис. 46). Рост изгибающего момента, в конце концов, может привести к разрушению балки — все зависит от величины зазора. Поэтому при подведении дополнительных опор зазоры необходимо устранять — подклиниванием стальными пластинами, подливкой бетона или др. способами. Только тогда опоры будут включены в работу.
6.3. Почему усиление целесообразно проводить при минимальном значении эксплуатационных нагрузок?
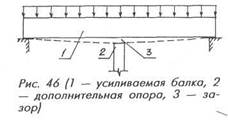
Для ответа на этот вопрос рассмотрим упомянутый выше пример усиления балки (рис. 47). Если дополнительную опору подводить тогда, когда на балку действует максимальная эксплуатационная нагрузка q и, следовательно, максимальный изгибающий момент Мmax(а), то опора работать не будет, усилие в ней будет равно нулю. Она сможет выполнить лишь противоаварийную задачу — удержать балку от обрушения. Если с балки снять часть нагрузки (б), то от оставшейся части q1 в балке возникает изгибающий момент М1. После подведения опоры и приложения ранее снятой нагрузки q2 балка начнет работать как двухпролетная и в ней возникнет дополнительный момент М2(в). Сумма этих моментов М(г) даст намного меньшее значение, чем Мmax. Понятно, что суммарная величина моментов будет тем меньше (а нагрузка на усиливающую конструкцию тем больше), чем больше величина снятой нагрузки q2?
Правда, в данном примере не следует впадать в другую крайность. Можно перед усилением так разгрузить балку (д), что в итоге в середине пролета возникнет отрицательный момент, который балка воспринять будет не в состоянии из-за недостаточного (или отсутствия) армирования верхней зоны, и вместо усиления балки произойдет ее разрушение. Поэтому при проектировании усиления всегда следует придерживаться правила: новая эпюра моментов не должна выходить за пределы эпюры материалов существующей конструкции.
6.4. Как следует подклинивать зазоры между усиливающей и усиливаемой конструкциями?
В этом деле опасно переусердствовать. При сильной забивке стальных пластин возникают большие расклинивающие усилия, причем усилия неконтролируемые, которые могут вызвать в усиливаемой конструкции опасные для нее изгибающие моменты. Особенно осторожно следует проводить усиление многопролетных неразрезных балок. Если при усилении балки одного из пролетов создать большое расклинивающие усилие, то в соседних пролетах изгибающие моменты возрастут, что может привести балки в аварийное состояние, — такие случаи в практике усиления встречаются. Поэтому толщину стальных клиньев (пластин) следует подбирать в соответствии с фактическими зазорами и забивать их легкими ударами молотка.
Необходимо помнить и о том, что в опорах (стойках) из монолитного железобетона или каменной кладки будут происходить усадочные процессы, особенно интенсивные в первые дни. Поэтому подклинивание зазоров нужно производить не ранее чем через неделю после возведения опор, а передачу дополнительной нагрузки — после набора бетоном или кладкой проектной прочности.
6.5. Чем отличаются жесткие опоры от упругих?
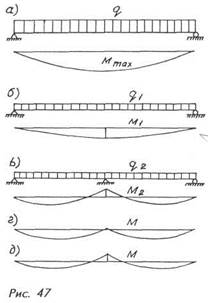
Жесткие — это опоры, которые не деформируются под нагрузкой (рис. 48, а). Упруго проседающими, или просто упругими, называются опоры, которые деформируются (проседают) под нагрузкой вместе с самой конструкцией (рис. 48, б). Деформации упругих опор зависят от величины нагрузки, от жесткости опирающейся конструкции (например, балки) и от жесткости самих опор. Чем меньше жесткость опоры, тем меньше опорная реакция R, тем меньше разгружается опирающаяся конструкция.
К жестким опорам обычно относят стойки (колонны) из кирпича, железобетона или металла, подкосы и т. п. элементы, которые подводят под усиливаемые конструкции и деформации которых настолько малы, что ими можно пренебречь. Однако подобные опоры имеют один существенный недостаток — они перегораживают помещения. Кроме того, опоры в виде стоек требуют устройства самостоятельных фундаментов. При этом следует иметь в виду, что основание под фундаментом в свою очередь подвергается деформациям (осадкам), в результате которых нагрузка на стойку уменьшается, а изгибающие моменты и поперечные силы в усиленной балке возрастают. Во избежание этого необходимо под подошвой фундамента либо предварительно обжимать грунт, либо устраивать большую песчано-щебеночную подушку. Поэтому, несмотря на всю простоту подобного усиления, его применяют довольно редко.
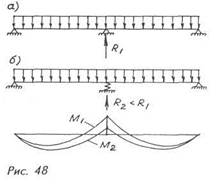
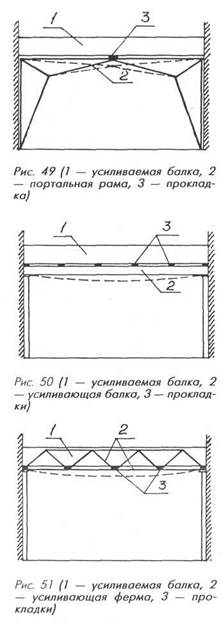
Указанных недостатков лишены портальные рамы (рис. 49), стальные балки (рис. 50), фермы (рис. 51), шпренгели и некоторые другие усиливающие конструкции. В процессе нагружения они подвергаются заметным деформациям (прогибам) совместно с усиливаемой конструкцией (пунктирные линии на рисунках), которыми пренебречь нельзя, не допустив грубейшую ошибку. Поэтому дополнительные опоры, которые образуют подобные конструкции, относятся к упругим.
6.6. Насколько эффективно усиление стальными балками?
Подведение стальных балок под железобетонные балки или плиты — довольно распространенный прием усиления. Основан он на принципе частичного разгружения — стальная балка является дополнительной (упругой) опорой и берет на себя часть полезной нагрузки. Однако эффективность такого усиления, как правило, невелика. Сечения стальных балок проектировщики зачастую подбирают простым суммированием несущих способностей усиливаемой и усиливающей балок: если существующая балка (плита) в состоянии воспринимать только часть расчетного изгибающего момента М, то сечение стальной балки подбирают из условия восприятия недостающей части.
Такой подход ошибочен по двум причинам. Во-первых, стальная балка включается в работу не с самого начала, а со времени приложения дополнительной нагрузки. Чем меньше разгружена железобетонная балка (плита), тем менее эффективно работает стальная балка (см. вопрос 6.3). Во-вторых, доли совместно воспринимаемой нагрузки определяются не несущими способностями сечений, а совместными деформациями (прогибом f). Поэтому дополнительная нагрузка распределяется пропорционально жесткостям существующей и усиливающей конструкций.
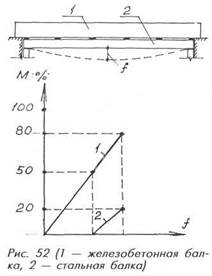
Поясним на примере (рис. 52). Железобетонная балка пролётом 6 метров имеет жесткость 81000 кН·м2 (при отсутствии трещин) и в состоянии воспринимать 80% расчетного изгибающего момента М = 290 кН·м. До начала усиления нагрузка на балку снижена наполовину, т.е. изгибающий момент в ней составляет 145 кН·м. Следовательно, из оставшейся половины изгибающего момента 30%М (ΔМb = 87 кН·м) должна воспринять железобетонная балка, а 20%M (Ms = 58 кН·м) - стальная. Поскольку прогибы балок одинаковы (fb = fs), пропорционально этим моментам должны быть и жесткости балок: ΔMb/Bb = Мs/Вs' откуда Bs/Bb = 2/3, т. е. жесткость стальной балки Bs = 54000 кН ·м2. Этой жесткости соответствует прокатный двутавр № 45, напряжения в котором при действии воспринимаемого им момента 58 кН·м составят 47 МПа, т. е. всего 1/5 расчетного сопротивления стали марки С235. Чем большая часть нагрузки снята с железобетонной балки до начала усиления, тем меньшее сечение потребуется для усиливающей балки и тем эффективнее она будет работать. Но даже при полном снятии нагрузки напряжения в последней (двутавр № 33а) составят всего 110 МПа.
Из приведенного примера видно, насколько неэффективно используется несущая способность усиливающей балки даже при самом раннем включении ее в работу. Правда, стальная балка будет нагружаться более интенсивно после образования трещин в железобетонной балке, когда жесткость последней заметно снижается. Однако строгий расчет их совместной работы затруднителен, а его результаты могут оказаться далекими от фактической работы.
6.7. Как повысить эффективность усиления изгибаемых элементов стальными балками?
Чтобы повысить эффективность работы стальных усиливающих балок, нужно создать предварительное напряжение: усиливающую (стальную) балку частично нагрузить, а усиливаемую (железобетонную) частично разгрузить — еще до того, как будет приложена дополнительная внешняя нагрузка.
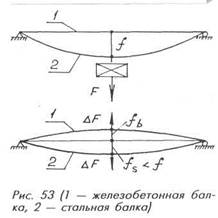
Выполнить предварительное напряжение можно разными способами. Один из них — оттянуть стальную балку книзу (прогнуть) с помощью подвешенных грузов, а в образовавшиеся между ней и железобетонной балкой зазоры вставить металлические распорки (пластины или пакеты из листов). После снятия грузов стальная балка стремится вернуться в исходное состояние (выпрямиться), но железобетонная этому препятствует. В результате, усиливающая балка нагружена силами, направленными сверху вниз, в усиливаемая — теми же силами, направленными снизу вверх (рис. 53). Правда, при этом часть преднапряжения стальной балки теряется (см. следующий вопрос).
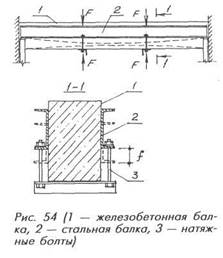
Потери напряжений можно исключить, если подобную операцию осуществлять с помощью гидродомкратов, устанавливаемых на усиливающую балку, с контролем усилий в них по манометру. При таком способе происходит одновременный выгиб железобетонной балки и прогиб стальной. Более простой способ — использование вместо домкратов натяжных или упорных болтов, усилия в которых контролируются по величине взаимного смещения f (суммы выгиба и прогиба) железобетонной и стальной балок (рис. 54).
Здесь не были упомянуты потери от обмятия контактных поверхностей, неизбежные при любом преднапряжении. При проектировании усиления их принимают обычно равными 20% начальной величины преднапряжения.
Приведенный пример показывает, что усиление можно выполнять и без разгружения железобетонной конструкции, если создать в ней усилия обратного знака за счет предварительного напряжения усиливающей конструкции.
6.8. Почему теряется часть предварительных напряжений в усиливающей балке при оттяжке ее грузами?
После снятия подвешенного груза F стальная балка жесткостью Bs, получившая прогиб f (рис. 53, а), стремится выпрямиться, т.е. полностью утратить начальные напряжения, но железобетонная жесткостью Bb этому препятствует — она выгибается на величину fb в то время как прогиб стальной балки уменьшается до величины fs (рис. 53, б). Поскольку fs < f/ происходит частичная потеря напряжений, в результате чего железобетонная балка разгружается не всей силой F, а только ее частью ΔF. Эта же часть нагружает и усиливающую балку. Величина Доопределяется следующим образом. Если пренебречь потерями напряжений от обмятия контактных поверхностей, то f = fb + fs. Тогда f = F(k/Bs), fb = ΔF(k/Bb), fs = ΔF(k/Bs), где k — условный коэффициент пропорциональности, зависящий от схемы приложения нагрузки (подвески грузов). Отсюда ΔF=FBb/(Bb+Bs). Следовательно, чем выше жесткость стальной балки по сравнению с железобетонной, тем меньше величина ΔF, тем больше потери напряжений.
6.9. Как работает шпренгель?
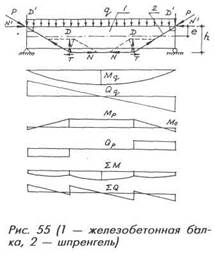
Шпренгель — это стержневая конструкция, в которой за счет совместных деформаций с усиливаемой железобетонной конструкцией возникает растягивающее усилие Р. Его горизонтальная проекция — распор N'=N—Т (где T — сила трения при перегибе стержней) создает положительный (загружающий) изгибающий момент Мо=N'·е, а вертикальные проекции D — отрицательный (разгружающий) момент Мp. Кроме того, в опорных участках возникают и разгружающие поперечные силы Qp, в результате чего суммарные усилия ΣM и ΣQ оказываются меньшими, чем усилия Мq и Qq от внешней нагрузки (рис. 55).
Целесообразно, казалось бы, концы шпренгеля опустить до уровня нейтральной оси усиливаемой балки, исключить образование в ней М0 и повысить, тем самым, эффективность усиления. Однако ожидаемого результата это не даст, поскольку одновременно уменьшатся значения D. Можно передвинуть весь шпренгель книзу, тогда и значения D сохранятся и M0 поменяет знак с положительного на отрицательный. Но в этом случае существенно усложняется конструкция шпренгеля, а сам он уменьшает полезный объем здания, поэтому такое решение широкого применения не нашло (а в зданиях с кранами вообще исключено).
В качестве шпренгельной затяжки используют стержневую арматурную сталь больших диаметров, а при необходимости — и прокатные профили из уголков или швеллеров. Как и в случае со стальными балками (см. вопрос 6.6), эффективность работы шпренгелей без предварительного напряжения весьма невелика. Опыт проектирования показывает, что если шпренгели включить в работу даже с самого начала (т. е. установить их при полностью снятой полезной нагрузке), то разгрузить железобетонные балки они в состоянии всего на 5...20%.
6.10. Как рассчитывают шпренгели?
Требуемую величину распора N определяют из величины требуемого уменьшения изгибающих моментов и поперечных сил на величину соответственно Мp и Qp (рис. 55). Далее необходимо найти, какая часть этого распора приходится на совместные деформации шпренгеля с балкой, а какая часть — на его преднапряжение. Точный расчет здесь довольно сложен, поскольку связан с поворотом торцов и линией прогибов балки, зависящих от схемы нагрузки, изгибной жесткости балки, осевой жесткости шпренгеля и др. факторов. Поэтому с достаточной для практики точностью пользуются приближенным расчетом: N = [(Mtot-M)/h+σspAss]γ £ 0,8 RsAss, где Мtot (на рис. 55 обозначен как Мq и М1 — изгибающие моменты после и до усиления, h — стрела провеса шпренгеля (плечо между N и N'), σsp — величина преднапряжения шпренгеля, Ass — площадь сечения стержней шпренгеля,
γss = 0,8 — коэффициент, учитывающий потери напряжений от обмятия контактных поверхностей, 0,8 — коэффициент условий работы стали. Приравняв выше найденную величину распора к этому выражению, можно определить величину усилия предварительного натяжения, а из нее и площадь сечения стержней шпренгеля. Если усиление проводится при действии полной нагрузки на балку, то первое слагаемое в квадратных скобках становится равным нулю и все усилие N создается только за счет преднапряжения шпренгеля. Саму балку после усиления рассчитывают по прочности как внецентренно сжатый элемент на действие сжимающей силы N' (распора за вычетом потерь от трения при перегибе) и изгибающего момента ΣМ.
6.11. Что дает усиление балок затяжками?
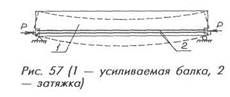
Продольные затяжки в виде арматурных стержней или прокатных профилей располагают вдоль растянутой грани балок и закрепляют на торцах. Под воздействием внешней нагрузки балка прогибается, а ее опорные сечения (торцы) поворачиваются (рис. 57). При повороте торцы увлекают за собой затяжку, удлиняют ее и вызывают в ней растягивающее усилие, которое, в свою очередь, действует на балку в виде сжимающей силы Р. От этой силы в балке возникает разгружающий момент Мp=-Ре, где е — расстояние от силы Р до центра тяжести сечения. В отличие от усиления шпренгелем, поперечные силы здесь не уменьшаются и разгружение опорных участков (наклонных сечений) не происходит.
Чем больше снято нагрузки с балки до начала усиления, тем больше последующие углы поворота торцов, тем больше и усилие Р. Разумеется, при этом требуется заранее устранить (выбрать) начальную слабину затяжки. Но даже и при условии полного предварительного снятия нагрузки напряжения в затяжке достигнут небольшой величины — как правило, не более 100 МПа. Ведь она работает как внешняя арматура без сцепления с бетоном, у которой растягивающие напряжения по длине постоянны, в то время как рабочая арматура балки в опасных сечениях испытывает куда более высокие напряжения. Поэтому в затяжках создают предварительное напряжение, которое позволяет значительно увеличить силу обжатия Р и, соответственно, увеличить разгружающий момент Mp.
Расчет затяжек можно выполнять приближенно. Из требуемой величины разгружающего момента Mp находят величину Р, а далее из выражения Р = [(100ΔMm/Mtot) + σsp] Assγss £ 0,8RsAss. находят требуемую площадь сечения Ass стержней затяжки, задавшись величиной их предварительного напряжения σsp. Здесь ΔMm и Мtot — величины соответственно дополнительного изгибающего момента, возникающего от прикладываемой после усиления нагрузки, и изгибающего момента от полной нагрузки (без учета Mp), γss=0,85 — коэффициент, учитывающий потери напряжений. Размерность в формуле приведена в Н и мм, при размерности в кг и см коэффициент 100 заменяется на 1 000.
Однако область применения затяжек относительно невелика, поскольку реальное опирание конструкций существенно отличается от идеального. В частности, у однопролетных железобетонных балок перекрытий и покрытий (а равно и ферм покрытий) в сборных каркасных зданиях опорные закладные детали приваривают к закладным деталям колонн, т. е. шарнирно-подвижные опоры у них отсутствуют. Это значит, что фактический поворот торцов меньше теоретического, а самое главное — расстояние между опорами, т. е. крайними точками нижней грани, остается неизменным. Поэтому даже предварительное напряжение затяжек такие конструкции практически не разгружает (почти все усилие Р передается не на растянутую зону, а на опорные закладные детали). Столь же бессмысленно усиливать затяжками многопролетные неразрезные балки и балки (ригели) монолитных рамных каркасов.
6.12. Как создают предварительное напряжение в шпренгелях и затяжках?
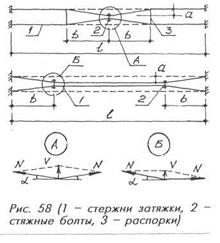
Усилие предварительного натяжения создают взаимным сближением (стягиванием) ветвей шпренгеля или затяжки с помощью стяжных болтов на величину а, по которой контролируют и величину самого усилия N. Как видно из рис. 58, а/b = tgα = i, тогда абсолютные деформации 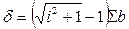 , относительные деформации ε=δ/I, а величина предварительного напряжения σsp=εЕ, где Σb — суммарная длина участков перегиба, Е — модуль упругости стали. Отсюда Nsp = σspAs, а усилие в стяжном болте V = 2Ni (схема "А") или V= Ni (схема "Б"). Проектное значение i назначается больше расчетного на 0,01 — величину, необходимую для выборки слабины ветвей.
, относительные деформации ε=δ/I, а величина предварительного напряжения σsp=εЕ, где Σb — суммарная длина участков перегиба, Е — модуль упругости стали. Отсюда Nsp = σspAs, а усилие в стяжном болте V = 2Ni (схема "А") или V= Ni (схема "Б"). Проектное значение i назначается больше расчетного на 0,01 — величину, необходимую для выборки слабины ветвей.
Ветви можно натягивать также с помощью домкратов и нарезных муфт, но в последнем случае для контроля величины σsp необходимо применять специальные приборы (а не динамометрические ключи, которые дают слишком большую погрешность). Независимо от способов натяжения, величина предварительного напряжения σsp не должна превышать 0,9Rsn для мягкой стали (имеющей физический предел текучести) и 0,7Rsn для высокопрочной стали. Максимальные напряжения в стержнях шпренгеля или затяжки (после вычета потерь напряжений и добавления напряжений от дополнительно приложенной нагрузки) должны быть не более 0,8Rs
Дата добавления: 2017-04-05; просмотров: 2469;











