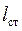ОСТОЙЧИВОСТЬ НА БОЛЬШИХ УГЛАХ НАКЛОНЕНИЯ
При изложении теории начальной остойчивости судна было отмечено, что допущение о линейной зависимости восстанавливающего момента от угла наклонения справедливо только для малых углов наклонения судна, за пределами которых плечо остойчивости и восстанавливающий момент уже не могут определяться метацентрическими формулами. Поэтому для характеристики остойчивости за пределами малых углов наклонения приходится прибегать к аппарату теории остойчивости на больших углах наклонения. При этом будем рассматривать только остойчивость при больших углах крена, поскольку большие углы дифферента у неповрежденного судна практически не возникают.
Говоря о наклонении судна в поперечной плоскости следует иметь ввиду ,что вследствие несимметрии судна относительно плоскости мидель-шпангоута центр величины выходит из плоскости наклонения и образуется вторая составляющая полного момента сил веса и плавучести – т.н. деривационный момент, действующий в продольной плоскости. Однако существенное различие между полным и восстанавливающим моментами, даже при больших углах крена, обнаруживается лишь в некоторых случаях наклонения поврежденного судна с затопленными отсеками. Для неповрежденного судна с достаточной для практических целей точностью можно считать, что остойчивость судна полностью определяется восстанавливающим моментом (действующим в плоскости наклонения) и ограничиться, поэтому, рассмотрением зависимостей, выражающих его величину при наклонении судна.
Прирассмотрении начальной остойчивости были приняты следующие основные допущения:
При крене судна перемещение центра величины происходит по дуге окружности;
Поперечный метацентр находится в точке, которая является центром этой окружности и не изменяет своего положения при наклонениях;
Значение поперечного метацентрического радиуса остается неизменным;
Равнообъемные ватерлинии пересекаются по прямой, проходящей через центр тяжести площади ватерлинии, расположенный в диаметральной плоскости судна.
Однако в процессе эксплуатации судна часто возникают наклонения на большие углы крена. В этих случаях применение перечисленных допущений приводит к неверным результатам. Поэтому и была разработана теория остойчивости судна при больших наклонениях.
При больших углах наклонения судно нельзя считать прямостенным в пределах изменения формы подводного объема: симметрия входящей ивыходящей частей площади наклонной ватерлинии значительно нарушается, что приводит к смещению оси пересечения двух равнообъемных ватерлиний. Перемещение центра величины при больших углах крена происходит уже не по дуге окружности, а по кривой переменной кривизны. Это равносильно тому, что поперечный метацентр не остается в постоянной точке m на диаметральной плоскости, как это было при малых углах крена, а смещается в новую точку m. Следовательно, и расстояние между метацентром и центром величины - поперечный метацентрический радиус – является переменной величиной. Положение центра тяжести площади действующей ватерлинии будет определяться только путем вычисления фактического положения равнообъемных ватерлиний. Т.о. переменность величины метацентрического радиуса можно объяснить и тем, что при крене судна форма площади действующей ватерлинии изменяется, ее продольная центральная ось наклонения смещается относительно диаметральной плоскости и, следовательно, значение момента инерции Ixx будет различным для каждой действующей ватерлинии.
Из сказанного следует, что метацентрическая высота уже не может служить критерием поперечной остойчивости. По этим соображениям, решая вопросы остойчивости при больших углах крена, нельзя пользоваться метацентрической формулой поперечной остойчивости и всеми полученными на ее основании формулами, в которые входит значение поперечной метацентрической высоты.
Под остойчивостью судна понимается его способность сопротивляться кренящим моментам. Но кренит судно, собственно,кренящий момент,а сопротивляетсяемувосстанавливающий момент.Поэтому восстанавливающим моментом и следует измерять остойчивость судна в этом случае.
Мерой статической остойчивости судна при больших углах крена будет являться восстанавливающий момент, равный:
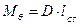 (3.1)
(3.1)
Основная задача расчета остойчивости при больших углах крена сводится к определению плеча lст восстанавливающего момента в зависимости от угла крена.
 m
m


 Л
Л 
 К
К








 В G Л
В G Л
 D
D

 а
а
 |


 z
z  N
N 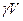





 C В C
C В C 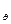
z 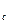 R
R
|
| |
| |

 Рис.3.1
Рис.3.1
При поперечном равнообъемном наклонении на угол 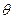 , на величину которого не накладываются какие-либо ограничения, центр тяжести судна не изменит своего положения, а центр величины
, на величину которого не накладываются какие-либо ограничения, центр тяжести судна не изменит своего положения, а центр величины  переместится в сторону наклонения. Метацентр также займет новое положение (Рис.3.1) Действующие на судно силы веса и плавучести направлены по нормалям к ватерлинии и образуют пару сил с плечом GK, значение которого уже нельзя выразить через поперечную метацентрическую высоту. Согласно рис.3.1 восстанавливающий момент можно представить как разность моментов силы плавучести
переместится в сторону наклонения. Метацентр также займет новое положение (Рис.3.1) Действующие на судно силы веса и плавучести направлены по нормалям к ватерлинии и образуют пару сил с плечом GK, значение которого уже нельзя выразить через поперечную метацентрическую высоту. Согласно рис.3.1 восстанавливающий момент можно представить как разность моментов силы плавучести 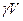 и силы веса D относительно первоначального положения центра величины С Плечо этой пары GK=
и силы веса D относительно первоначального положения центра величины С Плечо этой пары GK= 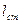 , как и ранее, назовем плечом статической остойчивости, а момент D
, как и ранее, назовем плечом статической остойчивости, а момент D 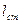 – восстанавливающим моментом
– восстанавливающим моментом
M 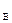 = D
= D 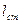 =
= 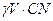 - D
- D 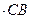 = D (CN-CB),
= D (CN-CB),
(3.2)
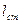 = CN – CB =l
= CN – CB =l 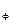 - l
- l 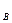 .
.
Отрезок l 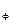 называют плечом остойчивости формы, так как при данном весе судна Р и угле крена
называют плечом остойчивости формы, так как при данном весе судна Р и угле крена 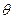 его значение зависит только от координат центра величины, определяемых формой подводного объема судна. Отрезок l
его значение зависит только от координат центра величины, определяемых формой подводного объема судна. Отрезок l 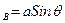 называют плечом остойчивости веса, так как при данном угле крена его длина зависит только от возвышения центра тяжести над центром величины. Соответственно момент
называют плечом остойчивости веса, так как при данном угле крена его длина зависит только от возвышения центра тяжести над центром величины. Соответственно момент 

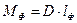 называют моментом остойчивости формы, а момент
называют моментом остойчивости формы, а момент 
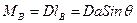 - плечом остойчивости веса.
- плечом остойчивости веса.
Иногда плечом остойчивости формы 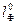 называют длину перпендикуляра OR, опущенного на линию действия силы плавучести из начала координат.
называют длину перпендикуляра OR, опущенного на линию действия силы плавучести из начала координат.
В этом случае плечо статической остойчивости веса будет 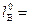
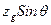 ,а плечо статической остойчивости выразится зависимостью
,а плечо статической остойчивости выразится зависимостью
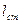 =
= 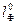 -
- 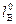 =
= 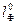 -
- 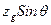 . (3.3)
. (3.3)
Разделение плеча остойчивости 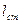 на две составляющие l
на две составляющие l 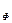 и l
и l 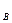 облегчает его вычисление, поскольку плечи формы могут быть вычислены заранее (в конструкторском бюро) и представлены в виде кривых в зависимости от водоизмещения судна и углов крена, а на судне для каждого угла крена необходимо только определить величину а возвышения ЦТ над ЦВ при данном состоянии нагрузки судна.
облегчает его вычисление, поскольку плечи формы могут быть вычислены заранее (в конструкторском бюро) и представлены в виде кривых в зависимости от водоизмещения судна и углов крена, а на судне для каждого угла крена необходимо только определить величину а возвышения ЦТ над ЦВ при данном состоянии нагрузки судна.
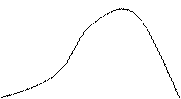
Диаграмма статической остойчивости.
Плечо восстанавливающего момента l и сам момент Мв имеют геометрическую интерпретацию в виде Диаграммы статической остойчивости (ДСО) (Рис.3.2). ДСО – это графическая зависимость плеча восстанавливающего момента l (θ) или самого момента Мв = 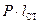 от угла крена θ.
от угла крена θ.
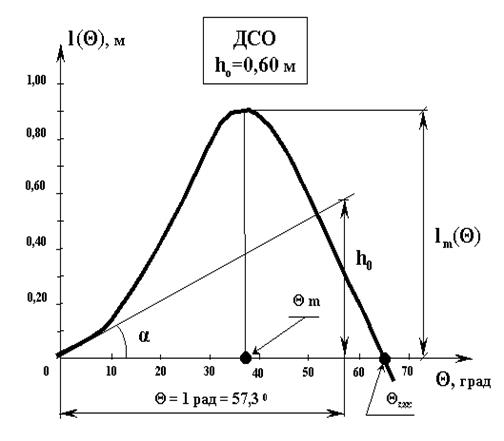 |
Рис. 4
Рис.3.2
Этот график, как правило, изображают для крена судна только на правый борт, поскольку вся картина при крене на левый борт для симметричного судна отличается только знаком момента Мв (θ).
Значение ДСО в теории остойчивости очень велико: это не только графическая зависимость Мв (θ); ДСО содержит в себе исчерпывающую информацию о состоянии загрузки судна с точки зрения остойчивости. ДСО судна позволяет решать многие практические задачи в данном рейсе и является отчетным документом для возможности начать загрузку судна и отправку его в рейс.
Диаграмма статической остойчивости имеет вид кривой с ярко выраженным максимумом. На ней можно отметить три точки, характерные для неповрежденного судна, обладающего положительной остойчивостью: точку О (начало координат), определяющую положение устойчивого равновесия; точку 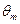 , где плечо статической остойчивости и восстанавливающий момент имеют максимальные значения, и точку
, где плечо статической остойчивости и восстанавливающий момент имеют максимальные значения, и точку 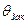 , определяющую т.н. угол заката диаграммы.
, определяющую т.н. угол заката диаграммы.
Равновесие накренившегося судна наступает при равенстве кренящего Мкр и восстанавливающего моментов Мв. Чтобы воспользоваться диаграммой статической остойчивости для определения угла крена, возникшего под действием заданного кренящего момента Мкр, необходимо найти плечо кренящего момента
Lкр = 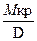 (3.4)
(3.4)
И условие равновесия судна можно записать в виде lкр=lв.
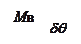 |
| |||




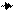




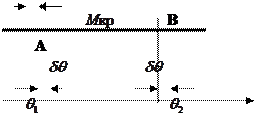 |
Рис.3.3
На диаграмме статической остойчивости в точке пересечения восстанавливающий момент равен кренящему и, следовательно, судно находится в равновесии в наклонном положении (см. Рис.3.3).
Но таких точек пересечения на ДСО будет две. Углу статического крена 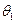 (положение устойчивого равновесия) будет соответствовать точка А.
(положение устойчивого равновесия) будет соответствовать точка А.
Отклонение от него в любую сторону на малый угол 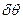 ведет к возникновению момента
ведет к возникновению момента 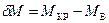 , стремящегося вернуть судно в исходное равновесное положение. Иная картина наблюдается в точке В – малейшее отклонение от нее на угол
, стремящегося вернуть судно в исходное равновесное положение. Иная картина наблюдается в точке В – малейшее отклонение от нее на угол 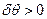 немедленно приводит к опрокидыванию судна, поскольку в области
немедленно приводит к опрокидыванию судна, поскольку в области 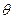 >
> 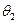 кренящий момент становится больше восстанавливающего; при отклонении на угол
кренящий момент становится больше восстанавливающего; при отклонении на угол 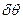 <0 наоборот,
<0 наоборот, 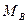 >
> 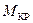 и под действием разницы моментов судно будет уходить из точки В в сторону уменьшения угла крена до тех пор, пока в точке А вновь не восстановится равновесие, теперь уже устойчивое. Нетрудно убедиться, что все точки равновесного положения накрененного судна приходящиеся на восходящую ветвь ДСО, соответствуют его устойчивому равновесию, и, наоборот, точки нисходящей ветви ДСО – соответствуют неустойчивому равновесию. Следовательно, по мере увеличения статического кренящего момента угол крена будет расти и опрокидывание произойдет, когда кренящий момент чуть – чуть превысит максимальный восстанавливающий момент, а угол опрокидывания будет равен углу максимума ДСО.
и под действием разницы моментов судно будет уходить из точки В в сторону уменьшения угла крена до тех пор, пока в точке А вновь не восстановится равновесие, теперь уже устойчивое. Нетрудно убедиться, что все точки равновесного положения накрененного судна приходящиеся на восходящую ветвь ДСО, соответствуют его устойчивому равновесию, и, наоборот, точки нисходящей ветви ДСО – соответствуют неустойчивому равновесию. Следовательно, по мере увеличения статического кренящего момента угол крена будет расти и опрокидывание произойдет, когда кренящий момент чуть – чуть превысит максимальный восстанавливающий момент, а угол опрокидывания будет равен углу максимума ДСО.
Диаграмма статической остойчивости строится для конкретного судна и соответствует определенным водоизмещению V и положению центра тяжести по высоте Zg. Если у данного судна изменится водоизмещение или аппликата центра тяжести, то ДСОприобретет другой вид. Это обстоятельство всегда надо иметь в виду. Каждое судно должно быть снабжено комплектом диаграмм статической остойчивости, характеризующих его остойчивость при наиболее часто встречающихся вариантах нагрузки. ДСОотличаются большим разнообразием форм кривых, но все они обладают некоторыми общими свойствами:
1.  Начальный участок ДСО представляет собой прямую наклонную линию. Действительно, при малых углах крена начальный участок диаграммы должен быть прямым, что можно доказать приравняв две формулы восстанавливающего момента: метацентрическую формулу поперечной остойчивости, применимую только для малых углов крена, и формулу восстанавливающего момента, справедливую для любых углов крена, т.е.
Начальный участок ДСО представляет собой прямую наклонную линию. Действительно, при малых углах крена начальный участок диаграммы должен быть прямым, что можно доказать приравняв две формулы восстанавливающего момента: метацентрическую формулу поперечной остойчивости, применимую только для малых углов крена, и формулу восстанавливающего момента, справедливую для любых углов крена, т.е. 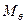 = Dh
= Dh 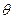 и
и 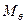 = Dlст, откуда lст= h
= Dlст, откуда lст= h 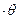 .
.
При малых углах крена поперечная метацентрическая высота h – постоянная величина, поэтому зависимость между плечом статической остойчивости и углом крена при малых значениях последнего является линейной и изображается прямой линией.
2.Отрезок перпендикуляра, восстановленного из точки на оси абсцисс, находящейся на расстоянии одного радиана от начала осей координат, до точки пересечения его с начальной касательной к кривой, определяет на ДСОначальную поперечную метацентрическую высоту h.
tg 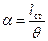 , но lст=h
, но lст=h 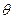 ; тогда tg
; тогда tg 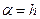 (3.5)
(3.5)
Однако графически определять метацентрическую высоту по ДСО не рекомендуется, т.к. проведение касательной к кривой не может быть выполнено с необходимой точностью. Указанное свойство ДСО применяют главным образом для контроля ее начального участка, когда известна поперечная метацентрическая высота.
В общем виде это свойство ДСО формулируется так: угловой коэффициент касательной к диаграмме в любой точке пропорционален т.н. «обобщенной» метацентрической высоте, соответствующей тому или иному значению угла крена, определяемому абсциссой точки касания.
Аналитически эти свойства выражаются производной от плеча остойчивости по углу крена, т.е. обобщенная метацентрическая высота выражается в виде:
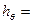
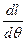 (Рис.3.4)
(Рис.3.4)
 | |||||
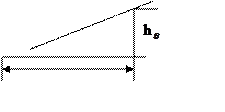 | |||||
| |||||
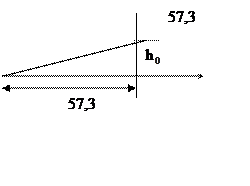 |
Рис.3.4
Вытекающие отсюда свойства ДСО таковы:
-.Для максимума диаграммы обобщенная метацентрическая высота равна нулю
-. Кривизна начальной ветви диаграммы позволяет судить о начальной остойчивости судна
3.Восходящая часть кривой диаграммы статической остойчивости характеризует устойчивое положение равновесия судна, а нисходящая – неустойчивое.
- ДСО конкретного судна зависит только от взаимного расположения центра тяжести судна G и начального поперечного метацентра m (или значения метацентрической высоты h0) и водоизмещения Р (или осадки dср) и учитывает наличие жидких грузов и запасов с помощью специальных поправок,
- форма корпуса конкретного судна проявляется в ДСО через плечо l(θ), жестко связанное с формой обводов корпуса, которое отражает смещение центра величины С в сторону входящего в воду борта при накренении судна,.
- метацентрическая высота h0, вычисленная с учетом влияния жидких грузов и запасов (см. ниже), проявляется на ДСО как тангенс угла наклона касательной к ДСО в точке θ = 0 (Рис.3.4), т.е.:

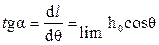 θ → 0 = h0 (3.4)
θ → 0 = h0 (3.4)
Для подтверждения правильности построения ДСО на ней делают построение: откладывают угол θ = 1 рад (57,30) и строят треугольник с гипотенузой, касательной к ДСО при θ = 0, и горизонтальным катетом θ = 57,30. Вертикальный (противолежащий) катет должен оказаться равным метацентрической высоте h0 в масштабе оси l(м).
- никакие действия не могут изменить вида ДСО, кроме изменения величин исходных параметров h0 и Р, поскольку ДСО отражает в каком-то смысле неизменную форму корпуса судна посредством величины l(θ);
- метацентрическая высота h0 фактически определяет вид и протяженность ДСО.
Угол крена θ = θ3, при котором график ДСО пересекает ось абсцисс, называется углом заката ДСО. Угол заката θ3 определяет только то значение угла крена, при котором сила веса и сила плавучести будут действовать вдоль одной прямой и l( θ3) = 0. Судить об опрокидывании судна при крене
θ = θ3 не будет верным, поскольку опрокидывание судна начинается гораздо раньше - вскоре после преодоления максимальной точки ДСО. Точка максимума ДСО (l = lm(θm)) свидетельствует только о максимальном удалении силы веса от силы поддержания. Однако, максимальное плечо lm и угол максимума θm являются важными величинами при контроле остойчивости и подлежат проверке на соответствие соответствующим нормативам.
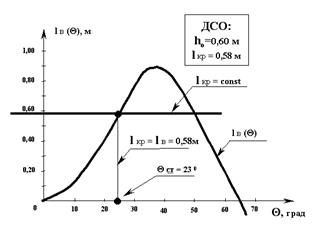 ДСО позволяет решать многие задачи статики судна, например, определять статический угол крена судна при действии на него постоянного (независящего от крена судна) кренящего момента Мкр = const. Этот угол крена может быть определен из условия равенства кренящего и восстанавливающего моментов Мв (θ) = Мкр. Практически эта задача решается как задача по нахождению абсциссы точки пересечения графиков обоих моментов (Рис.5).
ДСО позволяет решать многие задачи статики судна, например, определять статический угол крена судна при действии на него постоянного (независящего от крена судна) кренящего момента Мкр = const. Этот угол крена может быть определен из условия равенства кренящего и восстанавливающего моментов Мв (θ) = Мкр. Практически эта задача решается как задача по нахождению абсциссы точки пересечения графиков обоих моментов (Рис.5).
Рис.3.5 Взаимодействие кренящего и восстанавливающего моментов.
Диаграмма статической остойчивости отражает возможность судна создавать восстанавливающий момент при наклонении судна. Её вид имеет строго конкретный характер, соответствующий параметрам загрузки судна только в данном рейсе (Р = Рi , h0 = h0i). Судоводитель, занимающийся на судне вопросами планирования рейса погрузки и расчетами остойчивости, обязан построить конкретную ДСО для двух состояний судна в предстоящем рейсе: с неизменным первоначальным расположением груза и при 100 % и при 10 % судовых запасов.
Чтобы иметь возможность строить диаграммы статической остойчивости при различных сочетаниях водоизмещения и метацентрической высоты, пользуются вспомогательными графическими материалами, имеющимися в судовой документации по проекту этого судна, например, пантокаренами, либо универсальной диаграммой статической остойчивости.
Дата добавления: 2017-03-12; просмотров: 4555;