Изменение осадки судна при грузовых операциях

Любое изменение нагрузки приводит к изменению левой части уравнения ( 1.17 ), что автоматически отражается как на величине объемного водоизмещения , так и на осадке судна.

Очевидно, что прием груза p влечет за собой вхождение в воду дополнительного объема 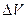, удовлетворяющего условию, аналогичному (1.17)

p = 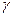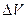. (1.22)

В свою очередь, если груз не очень велик, то изменение осадки 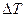будет также небольшим, в пределах которого площадь ватерлинии S практически останется постоянной. Тогда дополнительно вошедший в воду объем

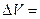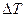S (1.23)

и с учетом (1.22 ) получим элементарную зависимость изменения осадки при приеме (снятии) груза 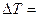p

p/ 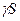(1.24 )

Два последних выражения, строго говоря, справедливы лишь для прямобортного (когда S 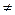f(T)) судна, однако практика показывает, что их использование не приводит к существенным ошибкам, если сила тяжести груза не превышает p = (10-12)%G.

Из (1.24), положив 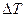= 1 см = 0,01 м, легко получить выражение для так называемого числа тонн на сантиметр осадки:

q = 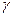S/ 100g (1.25)

Где q – масса груза, прием (снятие) которого приводит к изменению осадки на 1 см.

Тогда вместо (1/24) для практических расчетов удобно использовать формулу

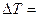m/q (1/26)

где m – масса принимаемого ( снимаемого ) груза.

Из ( 1/24 ) и (1/25 ) с ледует, что для решения задач, связанных с грузовыми операциями, необходима строевая по ватерлиниям.

Зависимости (1/24) и (1/26 ) используются для контроля осадки в процессе эксплуатации судна, учета влияния на осадку расходования топлива, воды и т.д.

Коэффициент полноты площади ватерлинии изменяется в достаточно узких пределах, поэтому, приняв его среднее значение равным 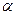= 0,78, с учетом (1/2 ) и(1/25 ) вместо (1/26 ) запишем:

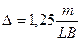м (1.27)

где m – масса груза, т; L, B – длина и ширина судна по рассматриваемую ВЛ, м.

Строго говоря, грузовая операция кроме изменения осадки в общем случае должна приводить и к появлению углов крена и дифферента, т.е. к изменению посадки в целом.

Для определения этих углов мы пока не обладаем достаточной информацией, поэтому сформулируем задачу иначе: какие условия должны быть выполнены, чтобы прием малого груза не сопровождался ни креном ни дифферентом?

Очевидно, что крен не появится, если ордината центра тяжести груза Yp=0, т.е.находится в ДП. Чтобы не возник дифферент, моменты силы тяжести груза и дополнительной силы плавучести должны быть равны, или ,другими словами, сила тяжести и сила плавучести должны лежать на одной вертикали. Поскольку дополнительный, входящий в воду объем, представляет собой призму, основанием которой является ватерлиния, то абсцисса центра тяжести этого объема равна абсциссе центра тяжести этого объема равна абсциссе центра тяжести площади ВЛ. Таким образом, для отсутствия дифферента необходимо выполнение условия

Xp = Xf . (1.28)

Сказанное справедливо для относительно небольшого груза. Когда груз велик, задачу проще и надежнее решать используя грузовой размер (рис 1.9 ),

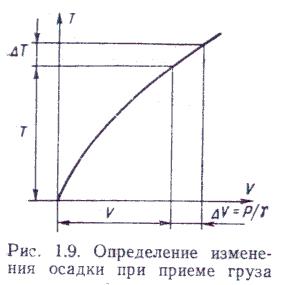
отложив на котором требуемое приращение подводного объема 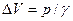, сразу найдем изменение осадки 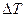(рис.1.9) .

Изменение осадки при изменении плотности воды.

Плотность забортной воды зависит главным образом от ее солености, а также от температуры. В ряде случаев морские транспортные суда принимают груз в портах с пресной водой, т. е. при р = 1,0 т/м3, и их осадка уменьшается после выхода в открытое море, где плотность воды может составлять 1,015-1,035 т/м3. Наибольшая допустимая осадка судна в морской воде задается “Правилами о грузовой марке морских судов”, поэтому для максимального использования грузоподъемности судна при его погрузке в пресной воде необходимо оценить уменьшение осадки при переходе из пресной воды в морскую.

Для решения этой задачи в самом общем случае предположим, что судно, имеющее объемное водоизмещение V в воде с плотностью 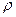, переходит в воду с плотностью 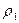, вследствие чего его объемное водоизмещение получает приращение 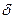V. Масса судна при этом не изменяется, следовательно,

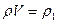(V + 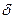V) (1.29)

Поскольку искомое изменение осадки 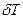относительно невелико (по сравнению с самой осадкой), то можно принять 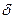V = S 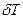, где S -площадь ватерлинии судна. Таким образом, уравнение (1.29) принимает вид

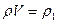(V + S 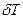) (1.30)

Решив это уравнение относительно 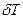, получим

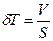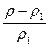* (1.31)

Подставляя в формулу (1.31) среднее (расчетное) значение плотности морской воды 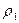= 1,025 т/м3 и принимая для пресной воды 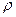=1,0 т/м3, а также подставляя S =100 q / 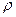согласно формуле (1.25), получим

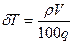
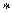
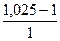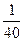
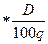
= (1.32)

или выражая 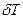в сантиметрах

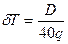(1,33)

Таким образом, осадка судна увеличивается на величину, определяемую формулой (1.33), при переходе из морской воды в пресную и уменьшается на ту же величину при переходе из пресной воды в морскую.