Колес с косыми зубьями.
Цилиндрическая передача, составленная из
Переходя к изучению косозубых передач, отметим прежде всего, что косые зубья располагаются на цилиндрах обоих колес по винтовым линиям (рис. 16.1). Если цилиндры развернуть на плоскость, то косые зубья (на развертке)окажутся расположенными по наклонным параллельным прямым. Так же будут расположены и косые зубья рейки.
|
 Косозубые колеса, как и прямозубые, изготовляются способом обкатки (см лекцию 14), в основу которого положен процесс станочного зацепления. Для нарезания применяется тот же стандартный инструмент, но устанавливается он на станке наклонно, под углом
Косозубые колеса, как и прямозубые, изготовляются способом обкатки (см лекцию 14), в основу которого положен процесс станочного зацепления. Для нарезания применяется тот же стандартный инструмент, но устанавливается он на станке наклонно, под углом 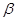 (рис. 16.2). Поэтому производящая зубчатая поверхность, которую в своем технологическом движении 3 описывают режущие кромки инструмента — гребенки Г, тоже будет наклонной. На рис. 16.2: производящая поверхность показана схематично в виденаклонно проецирующих линий. А так как эта поверхность (если ее мысленно сделать материальной) образует зубья воображаемой производящей рейки ПР то, следовательно, зубья рейки получатся косыми. Наглядно процесс обкатки можно представить себе как качение изготовляемогоколеса по производящей рейке ПР, имеющей косые зубья, наклоненные под углом
(рис. 16.2). Поэтому производящая зубчатая поверхность, которую в своем технологическом движении 3 описывают режущие кромки инструмента — гребенки Г, тоже будет наклонной. На рис. 16.2: производящая поверхность показана схематично в виденаклонно проецирующих линий. А так как эта поверхность (если ее мысленно сделать материальной) образует зубья воображаемой производящей рейки ПР то, следовательно, зубья рейки получатся косыми. Наглядно процесс обкатки можно представить себе как качение изготовляемогоколеса по производящей рейке ПР, имеющей косые зубья, наклоненные под углом 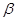 .
.
|
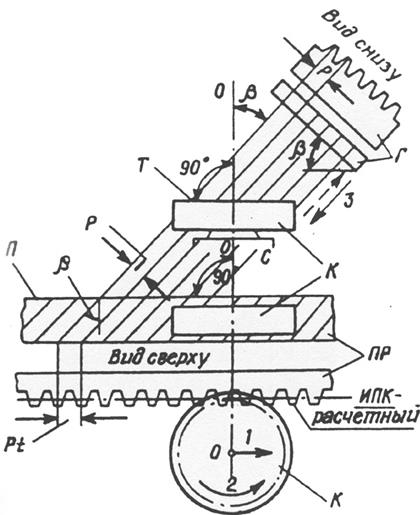 |
Такой же наклон получат зубья изготовляемого колеса на его станочно-начальном цилиндре. А так как в реечном станочном зацеплении делительный цилиндр совпадает со станочно-начальным, то именно на делительном цилиндре зубья получатся расположенными под углом
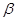 (см. рис. 16.1), на который наклонен инструмент на станке.
(см. рис. 16.1), на который наклонен инструмент на станке.
Из сравнения рис. 16.1 и 16.2 видно, что движения обката 1и 2 при изготовлении как прямозубых, так и косозубых колес одинаковы. А отсюда следует весьма важный вывод: все принципиальные положения, касающиеся станочного зацепления прямозубого колеса с прямозубой производящей рейкой
(см. лекцию 14), справедливы также для станочного зацепления косозубого колеса с косозубой производящей рейкой.
Вместе с тем процесс изготовления косозубых колес имеет и свои особенности, вытекающие из того, что инструмент установлен на станке наклонно. Определим, каким будет в этих новых условиях исходный производящий контур (ИПК), вступающий в станочное зацепление с профилем нарезаемых зубьев. Для этого рассечем наклонную зубчатую производящую поверхность плоскостью 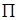 , перпендикулярной оси 00 колеса; в сечении получим искомый ИПК.
, перпендикулярной оси 00 колеса; в сечении получим искомый ИПК.
Нетрудно заметить, что благодаря наклону инструмента параметры полученного ИПК будут отличаться от параметров стандартного ИПК, который образуется при пересечении производящей поверхности плоскостью 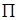 , ей перпендикулярной. Например, шаг pt нового ИПК составит pt = p/cos
, ей перпендикулярной. Например, шаг pt нового ИПК составит pt = p/cos 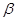 (рис. 16.2), где р -шаг стандартного ИПК. Поэтому mt = m/cos
(рис. 16.2), где р -шаг стандартного ИПК. Поэтому mt = m/cos 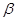 , где m -стандартный модуль инструмента. Чтобы в дальнейшем отличать стандартные параметры m,
, где m -стандартный модуль инструмента. Чтобы в дальнейшем отличать стандартные параметры m, 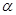 , h*a, c* от расчетных, будем присваивать последним значок t: mt,
, h*a, c* от расчетных, будем присваивать последним значок t: mt, 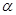 t, h*at, c*t. Следовательно, особенность станочного зацепления при изготовлении косозубых колес состоит в том, что благодаря наклонной установке инструмента ИПК не является больше стандартным, а становится расчетным.
t, h*at, c*t. Следовательно, особенность станочного зацепления при изготовлении косозубых колес состоит в том, что благодаря наклонной установке инструмента ИПК не является больше стандартным, а становится расчетным.
Здесь надо сделать принципиально важное добавление. Расчетный реечный ИПК (рис. 16.2), как и стандартный, имеет прямолинейные, т. е. эвольвентные, кромки. Поэтому в торцевой плоскости Т косозубого колеса (рис. 16.2) как и в любой, ей параллельной, зубья при изготовлении получают эвольвентный профиль. Но именно в этих плоскостях, перпендикулярных осям вращения колес проектируемой передачи, и происходит сам процесс зацепления профилей ее зубьев. Значит, косозубая цилиндрическая передача является эвольвентной передачей. Отсюда следует еще один важный вывод: все теоретические положения и зависимости, полученные ранее для прямозубой эвольвентной передачи полностью справедливы и для косозубой, но сформированной на базе расчетного ИПК. Поэтому математическая структура всех ранее составленных формул сохранится, но написание их будет иметь ту особенность, что всюду вместо стандартных параметров m, 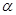 , h*a, c* в них надо подставлять расчетные параметрыmt,
, h*a, c* в них надо подставлять расчетные параметрыmt, 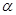 t, h*at, c*t, зависящие от угла
t, h*at, c*t, зависящие от угла 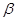 . Например:
. Например:
прямозубая передача:
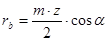
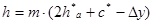
| косозубая передача:
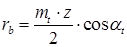
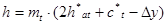
|
и т.п.
Укажем (без вывода) формулы перехода от стандартных параметров к расчётным:
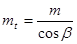 ,
, 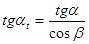 ,
, 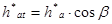 ,
, 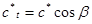 (16.1)
(16.1)
Косое направление зубьев наделяет цилиндрическую передачу особыми свойствами. Рассмотрим их. Благодаря наклону зуба он выходит из зацепления не сразу весь целиком, а постепенно. После того как профиль Эа выйдет из зацепления, шестерня 1повернется еще на угол 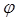
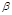 1. до момента выхода из зацепления профиля Эс (см. рис. 16.2). Продолжительность зацепления одной пары зубьев в косозубой передаче большая, чем в прямозубой, в которой зуб выходит из зацепления одновременно по всей своей длине. Поэтому угол поворота
1. до момента выхода из зацепления профиля Эс (см. рис. 16.2). Продолжительность зацепления одной пары зубьев в косозубой передаче большая, чем в прямозубой, в которой зуб выходит из зацепления одновременно по всей своей длине. Поэтому угол поворота 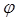
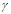 1 шестерни 1 за время полного зацепления одной пары косых зубьев составит уже не
1 шестерни 1 за время полного зацепления одной пары косых зубьев составит уже не 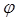
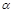 1, как в зацеплении прямых зубьев, a
1, как в зацеплении прямых зубьев, a
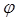
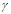 1 =
1 = 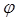
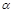 1 +
1 + 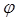
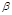 1
1
Коэффициентом перекрытия косозубой передачи называют отношение 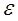
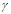 =
= 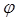
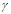 1/
1/ 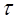 1 =
1 = 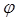
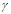 2/
2/ 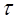 2.Раскроем его:
2.Раскроем его:
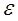
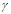 =
= 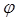
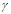 1/
1/ 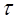 1 =
1 = 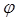
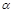 1/
1/ 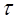 1 +
1 + 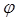
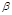 1/
1/ 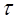 1 =
1 = 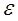
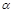 +
+ 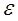
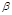
Слагаемое 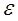
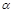 , называемое коэффициентом торцевого перекрытия, одсчитается по уравнению (15.8). Слагаемое
, называемое коэффициентом торцевого перекрытия, одсчитается по уравнению (15.8). Слагаемое 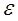
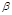 -коэффициент осевого перекрытия - определяется так:
-коэффициент осевого перекрытия - определяется так: 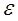
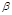 =
= 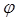
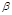 1/
1/ 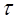 1 =A’C/AE= btg
1 =A’C/AE= btg 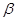 /pt(рис. 16.1)’
/pt(рис. 16.1)’
Подставив рt = 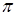 mt получим:
mt получим:
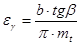 (16.2)[1]
(16.2)[1]
Теперь окончательно запишем формулу для определения коэффициента перекрытия косозубой передачи :
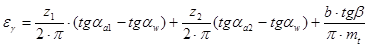 (16.3)
(16.3)
В прямозубой передаче (где 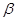 = 0) коэффициент осевого перекрытия
= 0) коэффициент осевого перекрытия 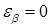 , так что
, так что 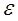
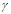 =
= 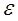
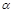 . Следовательно, коэффициент перекрытия косозубой передачи (где
. Следовательно, коэффициент перекрытия косозубой передачи (где 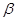
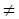 0) больше, а иногда и значительно больше коэффициента перекрытия прямозубой, что является достоинством косозубой передачи. Проф. Л. Н. Решетов рекомендует угол
0) больше, а иногда и значительно больше коэффициента перекрытия прямозубой, что является достоинством косозубой передачи. Проф. Л. Н. Решетов рекомендует угол 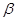 назначать так, чтобы получить для
назначать так, чтобы получить для 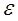
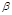 целое значение: 1, реже 2; это уменьшит износ зубьев.
целое значение: 1, реже 2; это уменьшит износ зубьев.
Для косозубых колес уравнение (15.) приобретает вид:
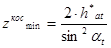
Так как, согласно формулам (15.) h*at < h*a, 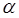 t >
t > 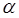 , zкосmin < zmin, т. е. косозубые колеса менее подвержены подрезанию, чем прямозубые.
, zкосmin < zmin, т. е. косозубые колеса менее подвержены подрезанию, чем прямозубые.
Л. Н. Решетов рассчитал и изготовил косозубую передачу, шестерня которой имеет вceгo один не пораженный подрезом зуб. Этим он наглядно и убедительно продемонстрировал возможность создания малогабаритных зубчатых передач (в том числе и прямозубых) путем снижения чисел зубьев менее zmin, не опасаясь их подрезания.
В лекциях 13…16 была кратко изложена геометрическая теория цилиндрической эвольвентной зубчатой передачи, которую с исчерпывающей полнотой разработал проф. В. А. Гавриленко [13] - основатель научной школы по зубчатым передачам.
Дата добавления: 2017-02-13; просмотров: 1365;











