Подрезание и заострение зуба.

Согласно свойствам эвольвентного зацеп­ления (см. лекцию 14) прямолинейная, т. е. эвольвентная, часть ИПК и эвольвентная часть профиля зуба колеса располагаются касательно друг к другу только на линии станочного зацепления, начинаю­щейся в точке N. Левее этой точки прямолинейный участок ИП не касается эвольвентного профиля зуба колеса, а пересекает его. Так как ИПК физически представляет собой тот след, который ре­жущая кромка инструмента оставляет на материале изготавли­ваемого колеса, то указанное пересечение приводит к подрезанию зуба колеса у его основания (рис. 15.1) Подрезание уменьшает эвольвентную часть профиля зуба колеса и ослабляет зуб в его опасном сечении.

Подрезание не происходит, когда граница В_l^', активной части линии станочного зацепления располагается правее точки N (см. рис. 14.6, a), т. е. когда выполняется условие:

P₀N 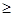P₀B_l^’(15.1)

Используя условие (15.1), определим минимальное число зубь­ев колеса, при котором они не будут подрезаны. Из 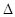P₀ON (см. рис. 14.6, а) следует, что P₀N = P₀O*sin 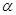, а из 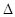P₀FB_l^’,что P₀ B_l^’ = P₀F/sin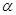

Подставляя величины P₀N и P₀B_l^’ в условие (15.1) и решая относительно z, имеем:

z 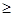2(h_a^* - x)/sin² 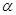(15.2)

Если x = 0, то из этого выражения получается минимальное число зубьев колеса без смещения, которые не будут подрезаны реечным инструментом

z_min = 2h_a^*/ sin² 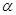(15.3)

При проектировании колес без смещения число зубьев необ­ходимо брать равным пли больше z_min. В случае стандартного инст­румента (h_a^* = 1,0; 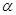= 20^o) z_min 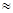17.

Для косозубых колес уравнение (15.3) приобретает вид:

z_min = 2h_a^* cos( 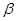)/sin²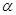

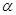Рис 15.1

Следовательно, косозубые колеса ме­нее подвержены подрезанию зубьев, поскольку _t > 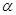, а cos 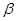< 1. В лекции 14 было указано, что для уменьшения габаритов зубчатых пере­дач колеса следует проектировать с малым числом зубьев. Однако при z < 17, чтобы не произошло подреза­ния, колеса должны быть изготовлены со смещением инструмента. Выясним, каково же то минимальное смещение, при котором не получается подрезания зубьев. Оно определяется также из выражения (15.1), на основании которого, используя (15.2), можно записать, что

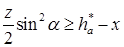
Подставляя сюда значение sin² 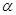из (15.3) и решая относитель­но х, имеем:

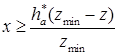(15.4)

а, переходя к минимальному значению x_min, получим формулу

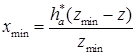(15.5)

Из зависимости (15.5) следует, что зубчатое колесо, имеющее z > z_min, можно нарезать с положительным, нулевым и даже с отри­цательным смещением, поскольку для такого колеса x_min < 0. Для зубчатого колеса, у которого z = z_min, можно взять положительное или нулевое смещение, а для колеса, у которогоz < z_min - только положительное смещение.

Если увеличивать коэффициент смещения, то толщина зуба s_a у вершины будет уменьшаться. При некотором коэффициенте смещения, называемом максимальным (x_min), наступает заострение зуба (s_a = 0). Опасность заострения особенно велика у колес с ма­лым числом зубьев (меньше 15).

Для предотвращения излома вершины заостренного зуба коэф­фициент смещения назначают так, чтобы толщина s_a была бы не меньше 0,2m (s_a > 0,2m). Толщину зуба s_aпри проектировании определяют по уравнению, положив r_y = r_a и 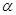_y = 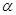_a ; соглас­но уравнению (14.2) cos 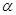_a = r_b/r_a.