Теорема 1. Для того, чтобы вектор был перпендикулярен заданной плоскости достаточно, чтобы он был перпендикулярен двум любым неколлинеарным векторам, лежащим в э той же плоскости.
ПЛОСКОСТЬ И ПРЯМАЯ В В ПРОСТРАНСТВЕ.
Чтобы зафиксировать плоскость в пространстве ОХУZ достаточно задать точку на ней и ненулевой вектор перпендикулярный плоскости. При выводе уравнения плоскости мы пользуемся следующим определением.
Определение 1. Вектор 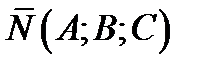 назовём вектором перпендикулярным плоскости, если он перпендикулярен любому вектору, лежащему в этой плоскости. Такой вектор называется нормальным вектором к данной плоскости.
назовём вектором перпендикулярным плоскости, если он перпендикулярен любому вектору, лежащему в этой плоскости. Такой вектор называется нормальным вектором к данной плоскости.
Теорема 1. Для того, чтобы вектор был перпендикулярен заданной плоскости достаточно, чтобы он был перпендикулярен двум любым неколлинеарным векторам, лежащим в э той же плоскости.
Точка принадлежит плоскости, тогда и только тогда, если координаты точки удовлетворяют уравнению плоскости.
Приступим к выводу уравнения плоскости. Сформулируем конечный результат.
Теорема 2. Плоскость, проходящая через точку 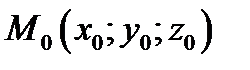 и имеющая нормальный вектор
и имеющая нормальный вектор 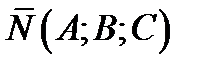 , задаётся уравнением
, задаётся уравнением
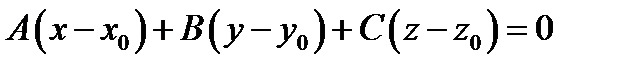 (1)
(1)
Доказательство. Нужно проверить, что если точка 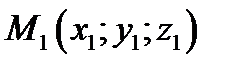 принадлежит нашей плоскости , то справедливо равенство
принадлежит нашей плоскости , то справедливо равенство 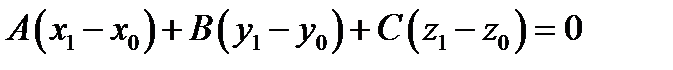 . Так как точки
. Так как точки 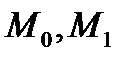 принадлежат плоскости, то вектор
принадлежат плоскости, то вектор 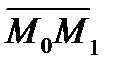 лежит на плоскости и по условию теоремы 2 он перпендикулярен нормальному вектору
лежит на плоскости и по условию теоремы 2 он перпендикулярен нормальному вектору 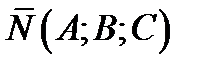 . Следовательно скалярное произведение равно нулю
. Следовательно скалярное произведение равно нулю
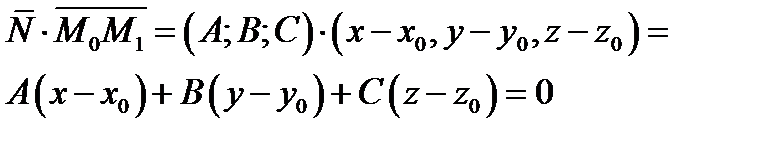
Рис.1
Отсюда и следует формула (1).
Пример 1. Написать уравнение плоскости проходящей через точку 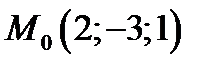 перпендикулярно вектору
перпендикулярно вектору 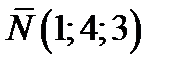 .
.
Решение. Согласно теореме.2 уравнение искомой плоскости задаётся формулой (1) 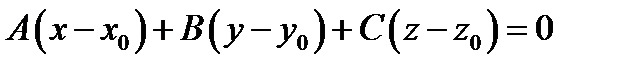 .Подставляя в неё данные задачи
.Подставляя в неё данные задачи 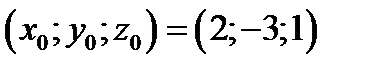 ,
, 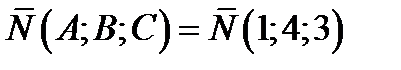 получаем ответ:
получаем ответ: 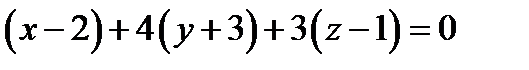 .
.
Таким образом если требуется найти уравнение плоскости, то из данных задачи нужно найти точку, через которую про ходит плоскость и любой вектор нормальный к данной плоскости .
Пример 2. Написать уравнение плоскости проходящей через точку 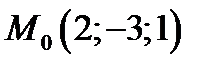 и параллельную векторам
и параллельную векторам 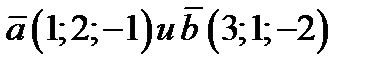 .
.
Решение. Для написания уравнения плоскости не хватает задания вектора нормального к плоскости. Векторы параллельные плоскости можно параллельным сдвигом расположить на плоскости. Вектор 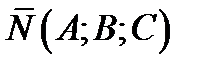 , перпендикулярный векторам
, перпендикулярный векторам 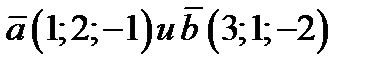 будет на основании теоремы 1 вектором нормальным к плоскости. Поэтому вектор
будет на основании теоремы 1 вектором нормальным к плоскости. Поэтому вектор 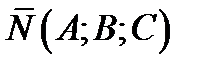 можно определить как векторное произведение векторов
можно определить как векторное произведение векторов 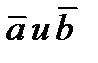
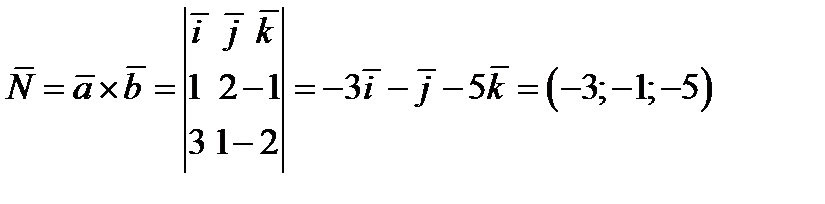
Отсюда по формуле (1) получаем искомое уравнение плоскости
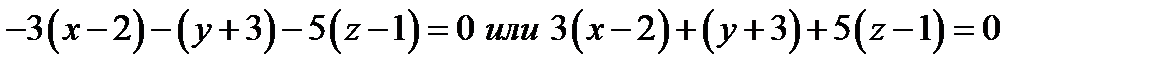
Замечание. Если в формуле (1) раскрыть скобки, то уравнение плоскости принимает вид
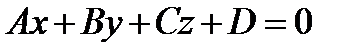 (2)
(2)
Такое уравнение плоскости называют общим уравнением плоскости.
Пример 3. Переписать уравнение плоскости 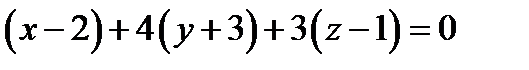 в общем виде.
в общем виде.
Решение. Раскрывая скобки, получаем ответ 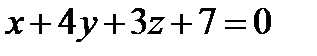 .
.
Приведем простые правила .
Правило 1. Условие параллельности двух плоскостей.Две плоскости 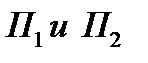 , имеющие коллинеарные нормальные векторы
, имеющие коллинеарные нормальные векторы 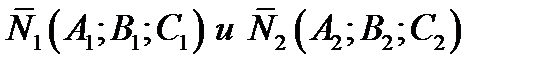 параллельны
параллельны
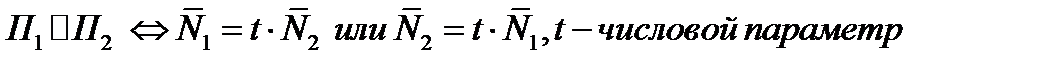 (3) или
(3) или
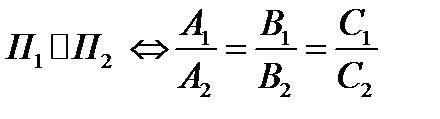 ( у коллинеарных векторов координаты пропорциональны) (4)
( у коллинеарных векторов координаты пропорциональны) (4)
Правило 2. Условие перпендикулярности двух плоскостей.Две плоскости 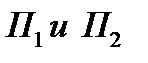 , имеющие перпендикулярные нормальные векторы
, имеющие перпендикулярные нормальные векторы 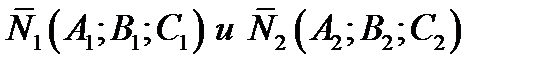 перпендикулярны
перпендикулярны
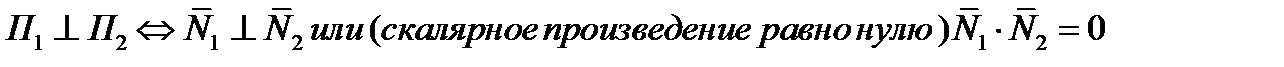 (5)
(5)
Правило 3. Вычисление значения линейного угла между плоскостями.Линейный уголмежду плоскостями 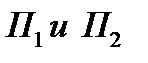 , имеющих нормальные векторы
, имеющих нормальные векторы 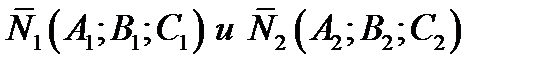 вычисляется по формуле
вычисляется по формуле
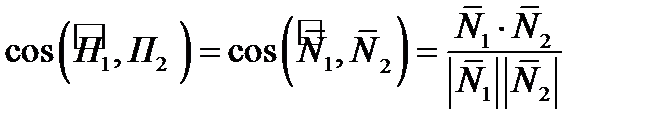 (6)
(6)
Пример 4. Проверить взаимное расположение плоскостей
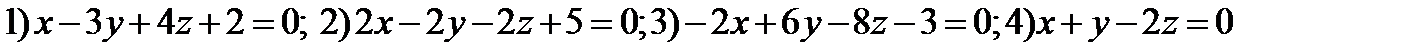
4) Вычислить угол между плоскостями 2) и 4).
Решение. Поскольку все вышеприведённые правила используют понятие нормального вектора к плоскости, то вычисляем эти нормальные вектора
-нормальный вектор к плоскости 1) равен 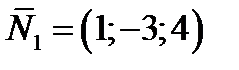 ;
;
- нормальный вектор к плоскости 2) равен 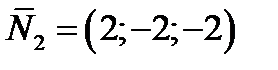 ;
;
- нормальный вектор к плоскости 3) равен 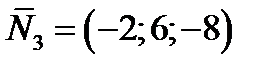 ;
;
- нормальный вектор к плоскости 4) равен 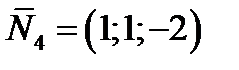 .
.
Отсюда :
1) векторы 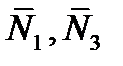 коллинеарные, так как по формуле (3) :
коллинеарные, так как по формуле (3) : 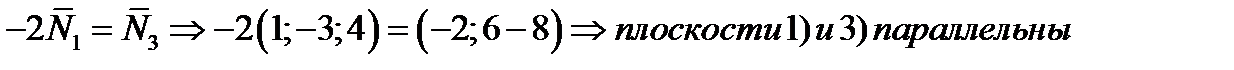
2) векторы 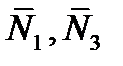 перпендикулярные, так как по формуле (4)
перпендикулярные, так как по формуле (4) 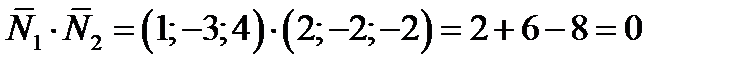
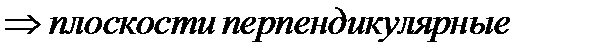 .
.
3) Вычислим угол между плоскостями 2) и 4)
Согласно формуле (5) получаем
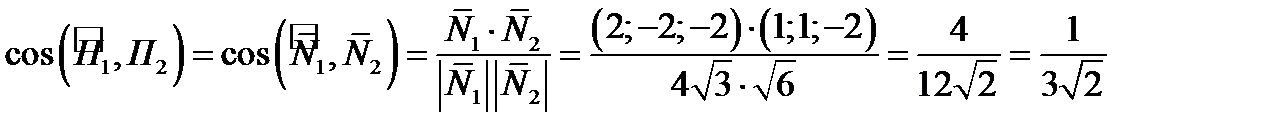
Используя калькулятор, находим угол: 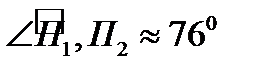 .
.
Прямые линии в пространстве 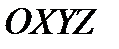
Для того чтобы получить уравнение наклонной прямой линии на плоскости 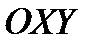 нам нужно было задать точку на прямой и наклон прямой к оси ОХ. Для того, чтобы получить аналогичное уравнение в пространстве необходимо задать точку
нам нужно было задать точку на прямой и наклон прямой к оси ОХ. Для того, чтобы получить аналогичное уравнение в пространстве необходимо задать точку 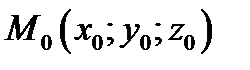 на прямой и ненулевой вектор
на прямой и ненулевой вектор 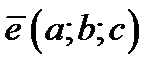 параллельный прямой. Вектор
параллельный прямой. Вектор 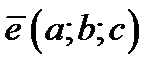 называют направляющим вектором прямой (см. рис.2).
называют направляющим вектором прямой (см. рис.2).
Наиболее простым способом задания прямой является параметрическое задание прямой. Способ задает систему уравнений, в которых координаты любой точки 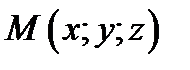 прямой являются функциями параметра
прямой являются функциями параметра 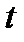 .
.
Теорема 5.3.Параметрические уравнения
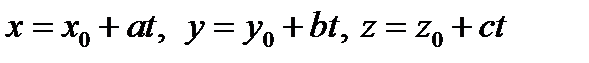 (7)
(7)
задают при любом значении параметра 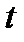 координаты точки
координаты точки 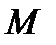
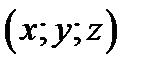 , лежащей на прямой.
, лежащей на прямой.
Доказательство. Докажем формулу (7). Пусть точка 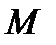
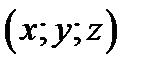 лежит на прямой, которая параллельна вектору
лежит на прямой, которая параллельна вектору 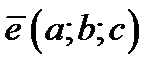 .Тогдавекторы
.Тогдавекторы 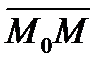 и
и 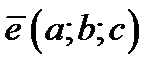 коллинеарные и следовательно
коллинеарные и следовательно
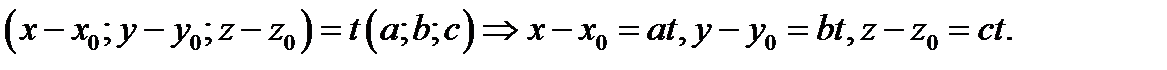
Отсюда следует формула (7).
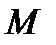

О
Рис.2
Записывая уравнения (7) в виде пропорций получаем канонические уравнения прямой
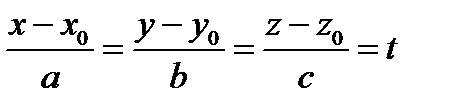 (8)
(8)
Пример 5. Написать параметрические уравнения прямой, проходящей через точку 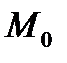
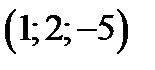 параллельно вектору
параллельно вектору 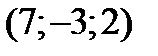 .
.
Решение. Подставляем данные примера в формулу (4), дающую параметрические уравнения прямой и записываем ответ: 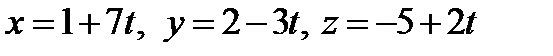 . Меняя
. Меняя 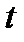 ,получаем различные точки на прямой. Взяв
,получаем различные точки на прямой. Взяв 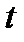 =3, получим точку
=3, получим точку 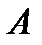
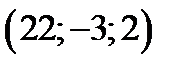 , лежащую на прямой правее точки
, лежащую на прямой правее точки 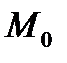
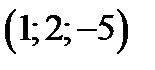 . Взяв
. Взяв 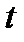 =-3, получим точку
=-3, получим точку 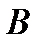
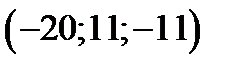 , лежащую на прямой левее точки
, лежащую на прямой левее точки 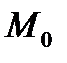
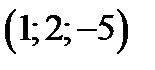 . Взяв
. Взяв 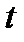 =0, получим точку начальную точку
=0, получим точку начальную точку 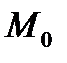
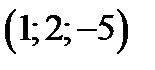 , лежащую на прямой.
, лежащую на прямой.
Пример 6. Написать уравнение прямой, проходящей через заданные точки А 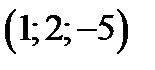 и В
и В 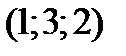 .
.
Решение. Согласно условиям теоремы 3 нам не хватает вектора параллельного прямой. Но из условия задачи его легко получить. Можно взять вектор 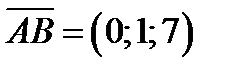 . Тогда из формулы (7)
. Тогда из формулы (7)
получаем параметрические уравнения прямой 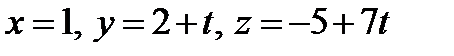 . В уравнениях
. В уравнениях
за начальную точку взята точка А 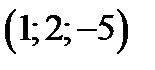 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| TRIAL ELIGIBILITY CRITERIA: COMMON COLD | | | Экономическое обоснование проекта. |
Дата добавления: 2016-06-05; просмотров: 5504;










