Теория теплообмена, или теория теплопередачи
Теория теплообмена,илитеория теплопередачи – это наука о самопроизвольных и необратимых процессах распространения теплоты, обусловленных неоднородным температурным полем.
Изучение данной теории в пожарном деле помогает выяснить закономерности переноса теплоты в телах и между телами, в результате чего появляется возможность нахождения распределения температур в объекте исследования как во времени, так и по координатам. Это, в свою очередь, позволяет решать вопросы, связанные с
· моделированием пожаров в помещениях;
· тепломассообменом при пожарах;
· причинами возникновения пожаров;
· возгораемостью и огнестойкостью конструкций;
· определением безопасных расстояний от очага пожара;
· профилактикой пожаров и т. д.
Процессы теплопередачи всегда протекают только при наличии разности температур между конкретными телами или частями вещественной среды. Таким образом, основной задачей исследования является определение температурного поля, которое в общем случае описывается следующим уравнением:
t =f (x, y, z, 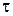 ), (2.1)
), (2.1)
где x, y, z – координаты точек тела, 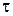 – время.
– время.
Известны три способа теплообмена: теплопроводность, конвективный теплообмен и лучистый теплообмен.
Перенос теплоты может происходить как с помощью отдельно взятого механизма теплопроводности, конвекции или излучения, так и
в любой комбинации из них. Каждый из этих способов переноса подчиняется своим законам, поэтому при изучении процесса теплопередачи рассматривают порознь явления теплопроводности, конвекции и излучения.
ТЕПЛОПРОВОДНОСТЬ
Теплопроводностьюназывают молекулярный перенос тепла микрочастицами, вызванный разностью температур. Процесс теплопроводности наблюдается в твердых телах, в тонких слоях жидкости и газов, но
в наиболее чистом виде в твердых телах.
Молекулы, атомы, электроны и др. микрочастицы, движутся со скоростями, пропорциональными их температуре. За счет взаимодействия друг с другом быстродвижующиеся микрочастицы отдают свою энергию более медленным, передовая таким образом теплоту из зоны с высокой в зону с более низкой температурой.
Втвердых металлических телах теплопроводность происходит в следствии движения свободных электронов.
Внеметаллических твердых телах (в частности, изоляционных материалах), в которых практически отсутствуют свободные электроны, перенос теплоты осуществляется за счет колебаний атомов и молекул.
Вгазах микроструктурным движением является беспорядочные молекулярные движения, интенсивность которых возрастает с увеличением температур.
В основе теории теплопроводности в твердых телах лежит закон Фурье:
Q = - 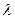
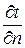 F, (2.2)
F, (2.2)
где Q – количество переданного тепла в единицу времени, Вт; 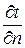 – градиент температур,
– градиент температур, 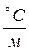 ; n – нормаль к изотермической поверхности тела; F – площадь, перпендикулярная к направлению распространения тепла, м2;
; n – нормаль к изотермической поверхности тела; F – площадь, перпендикулярная к направлению распространения тепла, м2; 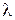 – коэффициент теплопроводности,
– коэффициент теплопроводности, 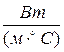 .
.
Коэффициент теплопроводностиl, характеризующий способность данного вещества проводить теплоту, зависит как от его природы, так и от агрегатного состояния.
Значительное влияние на коэффициент теплопроводности могут оказывать температура, а у пористых материалов еще и влажность.
Значения 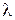 для различных тел в зависимости от температуры приводятся в справочной литературе.
для различных тел в зависимости от температуры приводятся в справочной литературе.
При исследовании процесса теплопроводности в твердых телах пользуются дифференциальным уравнением Фурье-Кирхгофа:
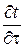 =a(
=a( 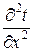 +
+ 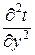 +
+ 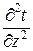 ), (2.3)
), (2.3)
где а= 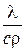 ,
, 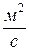 , –коэффициент температуропроводности.
, –коэффициент температуропроводности.
Коэффициент температуропроводности является физической величиной, характеризующей скорость изменения температуры в данном веществе.
Если температурное поле не зависит от времени, то оно называется стационарным и описывается следующим уравнением:
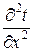 +
+ 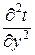 +
+ 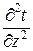 = 0. (2.4)
= 0. (2.4)
Это уравнение является исходным при решении задач стационарной теплопроводности. Например, из этого уравнения получаются выражения для температурных полей в однослойной стенке:
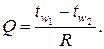 (2.5)
(2.5)
Здесь R – термическое сопротивление:
· в случае плоской стенки:
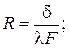 (2.6)
(2.6)
· в случае цилиндрической стенки:
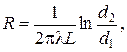 (2.7)
(2.7)
где: 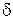 – толщина плоской стенки; d1, d2 –внешний и внутренний диаметры цилиндра; L – длина цилиндра;
– толщина плоской стенки; d1, d2 –внешний и внутренний диаметры цилиндра; L – длина цилиндра; 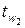 ,
, 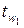 – температура на внешней и внутренней поверхностях тела.
– температура на внешней и внутренней поверхностях тела.
КОНВЕКЦИЯ
Конвекцией называется процесс распространения тепла в жидкости от поверхности твердого тела или к его поверхности, одновременно конвекцией и теплопроводностью.
Под жидкостью здесь понимают не только капельную жидкость,
но и газ.
В процессе конвективного теплообмена задействованы два различных механизма переноса теплоты, по причине образования непосредственно у твердой поверхности из-за действия сил вязкого трения тонкого слоя заторможенной жидкости (пограничного слоя). В следствии этого, теплота, прежде чем распространиться от поверхности тела к жидкости (в случае, если температура поверхности выше температуры жидкости), сначала должна за счет теплопроводности пройти через пограничный слой, а затем уже от пограничного слоя попасть в массу (ядро) жидкости с помощью конвекции.
При решении инженерных задач для расчета конвективного теплообмена между поверхностью твердого тела и жидкостью используют закон Ньютона-Рихмана:
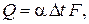 (2.8)
(2.8)
где a – коэффициент теплоотдачи, 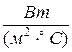 , характеризующий интенсивность передачи теплоты; F – площадь теплоотдающей поверхности, м2; Dt – разность температур [либо Dt=(tw-tf), либо Dt=(tf-tw), в зависимости от направления теплового потока], °С; t w – температура поверхности тела, °С; t f – температура жидкости за пределами пограничного слоя, °С.
, характеризующий интенсивность передачи теплоты; F – площадь теплоотдающей поверхности, м2; Dt – разность температур [либо Dt=(tw-tf), либо Dt=(tf-tw), в зависимости от направления теплового потока], °С; t w – температура поверхности тела, °С; t f – температура жидкости за пределами пограничного слоя, °С.
Коэффициент теплоотдачи показывает, какое количество теплоты передается от теплообменной поверхности к 1 м2 в жидкость или, наоборот, от жидкости к теплообменной поверхности 1 м2 в единицу времени при разности температур теплообменной поверхности и жидкости
в 1 градус.
Вся сложность расчета конвективного теплообмена и состоит
в определении коэффициента теплоотдачи.
Величина a зависит от всех факторов, влияющих на сам процесс теплообмена. К ним относятся скорость движения жидкости, физические свойства теплоносителя, гидродинамические характеристики потока, геометрическая форма и размеры поверхности теплообмена и др.:
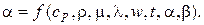 (2.9)
(2.9)
При изучении конвективного теплообмена большую помощь оказала теория подобия, на основе которой были установлены группы подобных явлений и обобщенные переменные – числа (критерии) подобия, характеризующие данную группу явлений. Эти числа подобия составляются из различных физических параметров и они безразмерны.
В случае конвективного теплообмена наиболее часто используются следующие числа подобия:
· число Нуссельта определяющее интенсивность теплообмена:
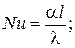 (2.10)
(2.10)
· число Прандтля характеризующее физические свойства жидкости:
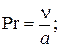 (2.11)
(2.11)
· число Грасгофа характеризует интенсивность свободного движения:
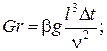 (2.12)
(2.12)
· число Рейнольдса характеризует гидродинамический режим движения потока жидкости:
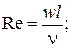 (2.13)
(2.13)
· число Кутателадзе-Кружилина является мерой отношения плотности теплового потока, расходуемого на фазовое превращение вещества, к теплоте перегрева (переохлаждения) одной из фаз
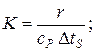 (2.14)
(2.14)
· число Галилея является мерой отношения сил тяжести и молекулярного трения в потоке:
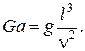 (2.15)
(2.15)
В эти выражения входят следующие величины:
a – коэффициент конвективной теплоотдачи, 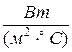 ;
;
l – определяющий размер тела, м;
l – теплопроводность жидкости, 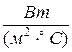 ;
;
n – кинематическая вязкость жидкости, 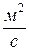 ;
;
g – ускорение свободного падения, 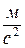 ;
;
а– коэффициент температуропроводности жидкости, 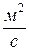 ;
;
b – температурный коэффициент объемного расширения, 1/К (для газов b =1/Тf, для жидкостей значения берутся из справочной литературы);
w – скорость потока жидкости, 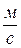 ;
;
r – удельная теплота парообразования, 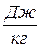 ;
;
cр – удельная теплоемкость жидкости, 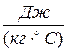 ;
;
Dt – разность температур [либо Dt = (tw- tf ), либо Dt =(tf - tw) в зависимости от направления теплового потока], °С;
t w – температура поверхности тела, оС;
tf – температура жидкости за пределами пограничного слоя, оС;
Dts – разность температур [либо Dt = (tw-ts), либо Dt =(ts-tw) в зависимости от направления теплового потока], оС;
t s – температура фазового превращения, оС .
В зависимости от геометрической формы поверхности теплообмена,
в качестве определяющего размера l, выбирают следующие параметры:
· для труб и шаров определяющим линейным размером является диаметр d;
· для вертикальных труб большого диаметра и пластин – высота H;
· для горизонтальных плит – наименьший размер плиты (если греющая сторона плиты обращена вверх, то значение коэффициента A необходимо увеличить на 30% по сравнению с приведенным, если греющая сторона обращена вниз, то значение A следует уменьшить на 30%).
Так как входящие в числа подобия (2.10)-(2.15) физические величины зависят от температуры, значения этих чисел рассчитываются при температуре, называемой далее определяющей.
В соответствии с этим числа подобия снабжаются индексами w, f или m (w – признак температуры твердой поверхности тела, т. е. определяющей температурой в этом случае является температура поверхности тела;
f– признак температуры жидкости; m – признак среднего значения температуры).
Классификация задач по условиям конвективного теплообмена позволила выделить два основных вида конвективного теплообмена (рис. 2.1):
· теплообмен без изменения агрегатного состояния (вынужденная конвекция и свободная конвекция) вещества;
· теплообмен при изменении агрегатного состояния(кипение и конденсация) вещества.
В свою очередь каждый из этих видов конвективного теплообмена (кипение, конденсация, вынужденная и свободная конвекция) имеют свои разновидности.
Для примера, можно показать порядок величиныa, 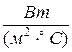 , для различных условий конвективного теплообмена:
, для различных условий конвективного теплообмена:
свободная конвекция в газах 5, …, 30;
свободная конвекция для воды 102, …, 103;
вынужденная конвекция газов 10, …, 500;
вынужденная конвекция для воды 500, …, 104;
теплообмен при изменении агрегатного состояния воды (кипение, конденсация) 103, …, 105.
В общем случае коэффициент теплоотдачи определяется как
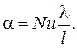 (2.16)
(2.16)
При решении задач на конвективный теплообмен, критерий Нуссельта чаще всего дается в критериальной форме в виде:
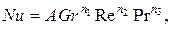 (2.17)
(2.17)
где показатели степеней n1, n2, n3 и множитель пропорциональности А были найдены путем обработки экспериментальных данных.
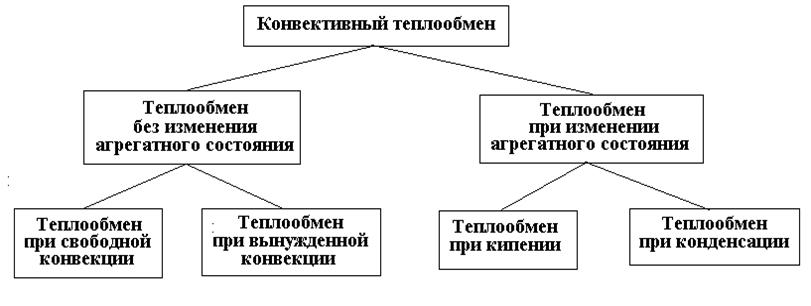
Рис. 2.1. Разновидности конвективного теплообмена
ИЗЛУЧЕНИЕ
Излучение – это перенос энергии электромагнитными волнами (этот процесс обусловлен превращением внутренней энергии вещества в энергию излучения, переносом излучением и его поглощением веществом).
Особенностью теплообмена излучением является то, что такой теплообмен не требует непосредственного контакта тел. Излучение рассматривается как процесс распространения электромагнитных волн, испускаемых телом. Излучение энергии сводится к преобразованию внутренней энергии тела в лучистую энергию электромагнитных колебаний. Излучение электромагнитных волн свойственно всем телам. Спектр излучения большинства твердых и жидких тел сплошной, непрерывный. Это значит, что эти тела обладают способностью излучать (и поглощать) лучи всех длин волн. Распределение энергии в спектре излучающего тела определяется температурой тела. Носителями тепловой лучистой энергии являются волны инфракрасной части спектра излучения с длиной волны 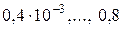 мм.
мм.
Суммарное излучение с поверхности тела по всем длинам волн спектра называется интегральным или полным лучистым потоком. При постоянной поверхностной плотности интегрального излучения Е0 (собственное излучение) излучающей поверхности F полный лучистый поток Q0, Вт, определяется соотношением:
Q0 = E0 F. (2.18)
В общем случае, при попадании лучистого потока на другие тела, эта энергия частично поглощается, частично отражается и частично проходит сквозь тело (рис. 2.2). Та часть лучистой энергии, которая поглощается телом, снова превращается в тепловую. Та же часть энергии, которая отражается, попадает на другие тела и ими поглощается. То же самое происходит и с той частью энергии, которая проходит сквозь тело.
Таким образом, после ряда поглощений излучаемая энергия полностью распределяется между окружающими телами. Следовательно, каждое тело не только излучает, но и непрерывно поглощает лучистую энергию.
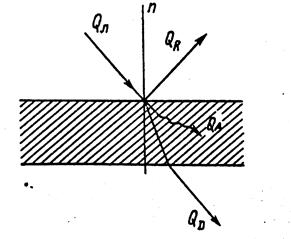
Рис. 2.2. Распределение лучистого потока, падающего на тело
На основании закона сохранения энергии можно написать:
Q0 = QA + QR + QD(2.19)
или для плотностей излучения:
E0 = EA + ER + ED. (2.20)
Здесь: 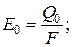
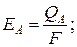
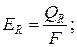
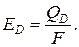
В безразмерном виде:
A + R + D = 1, (2.21)
где 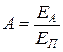 – коэффициент поглощения;
– коэффициент поглощения; 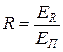 – коэффициент отражения;
– коэффициент отражения; 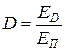 – коэффициент проницаемости.
– коэффициент проницаемости.
Коэффициенты поглощения, отражения и проницаемости зависят от природы тел, состояния их поверхности. Как видно из формулы (2.21), их значения могут изменяться в пределах от 0 до 1.
Тело, которое полностью поглощает всю падающую на него лучистую энергию, т. е. А=1, D=R= 0, называют абсолютно чернымтелом.
Если R=1, А = D = 0, то такое тело называют абсолютно белым
телом (вся энергия отражается).
Если D=1, A= R = 0 – абсолютно прозрачнымтелом (вся энергия проходит насквозь).
Значения A, R и D зависят от природы тела, его температуры и длины волны излучения. Воздух, например, для тепловых лучей прозрачен, но при наличии в воздухе водяных паров или углекислоты он становится полупрозрачным.
Большинство твердых и жидких тел для тепловых лучей практически непрозрачны, т. е. D = 0:
A+R=1.
Однако, имеются тела, которые прозрачны лишь для определенных длин волн. Так, например, кварц для лучей с длинами волн более 0,04 мм, непрозрачен, а для световых и ультрафиолетовых лучей прозрачен. Оконное стекло прозрачно только для световых лучей, а для ультрафиолетовых и тепловых оно почти не прозрачно.
Точно также обстоят дела с понятиями поглощения и отражения. Белая поверхность хорошо отражает лишь видимые (солнечные) лучи.
В жизни это свойство широко используется: белые летние костюмы, белая окраска цистерн и т. д. Невидимые же тепловые лучи белая ткань и краска поглощает также хорошо, как и темная.
Для поглощения и отражения тепловых лучей большее значение имеет не цвет, а состояние поверхности. Независимо от цвета отражательная способность гладких и полированных поверхностей во много раз выше, чем у шероховатых.
В природе абсолютно черных, белых и прозрачных тел не сущест
вует. Наиболее близки к абсолютно черному телу сажа и бархат
(А=0,97, ..., 0,98), к абсолютно белому телу – полированные металлы (R=0,97). Одно- и двухатомные газы практически прозрачны.
Тела, у которых коэффициент поглощения 0<А<1 и поглощательная способность не зависит от длины волны падающего излучения, называются серыми телами. Большинство твердых тел можно рассматривать как серые тела.
Излучение абсолютно черного тела подчиняется следующим законам:
· закон Планка, устанавливающий зависимость между интенсивностью излучения J0, длиной волны 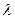 и термодинамической температу-
и термодинамической температу-
рой Т:
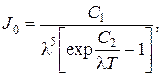 (2.22)
(2.22)
где С1 и С2 – постоянные величины;
· закон Вина, исходя из закона Планка, дает зависимость 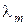 от Т:
от Т:
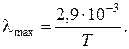 (2.23)
(2.23)
Из формулы (2.21) видно, что с повышением температуры длина волны, соответствующая максимальной интенсивности излучения, смещается в сторону более коротких длин волн.
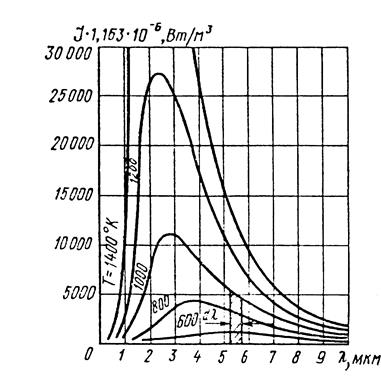
Рис. 2.3.Зависимость спектральной интенсивности излучения
абсолютно черного тела от длины волны и температуры
· Закон Стефана-Больцмана дает возможность определить плотность лучистого потока Е0 абсолютно черного тела:
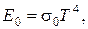 (2.24)
(2.24)
где 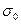 = 5,67 10-8 Вт/(м2 К) – константа излучения абсолютно черного тела.
= 5,67 10-8 Вт/(м2 К) – константа излучения абсолютно черного тела.
В технических расчетах закон Стефана-Больцмана удобно применять в форме:
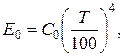
где 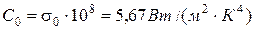 – коэффициент излучения абсолютно черного тела.
– коэффициент излучения абсолютно черного тела.
Для серых тел, у которых интенсивность излучения меньше, чем
у черных тел при той же температуре, Е<E0.
Отношение 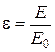 называют степенью черноты серого тела.
называют степенью черноты серого тела.
Пользуясь понятием о степени черноты, плотность лучистого потока для серого тела можно выразить следующим уравнением:
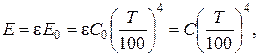 (2.25)
(2.25)
где 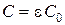 - коэффициент излучения серого тела.
- коэффициент излучения серого тела.
· Закон Кирхгофа устанавливает связь между излучательной и поглощательной способностью тел.
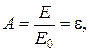 (2.26)
(2.26)
т. е. коэффициент поглощения численно равен степени черноты данного тела.
· Закон Ламберта дает возможность определить зависимость изменения энергии лучистого потока от его направления по отношению к поверхности тела. Наибольшей интенсивностью обладает излучение по нормали к поверхности Еп. По остальным направлениям оно меньше, равно 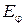 и выражается формулой:
и выражается формулой:
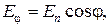 (2.27)
(2.27)
где 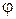 – угол между направлением излучения и нормалью (рис. 2.4).
– угол между направлением излучения и нормалью (рис. 2.4).
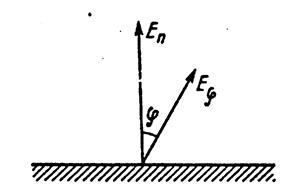
Рис. 2.4. К выводу закона Ламберта
Если два тела с температурой T1 и T2 обмениваются лучистой энергией, разделены прозрачной средой, то тепло, переданное излучением, можно определить из выражения:
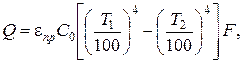 (2.28)
(2.28)
где 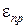 – приведенная степень черноты.
– приведенная степень черноты.
В случае, когда одно тело окружено другим, то
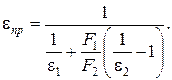 (2.29)
(2.29)
Если два тела расположены в пространстве произвольно, причем лучистый поток от одного тела не полностью попадает на другое, то в выражение для теплообмена между телами вместо F войдет величина F1-2, называемая взаимной поверхностью излучения. В этом случае расчет теплообмена сводится к определению F1-2.
Коэффициент теплоотдачи излучением равен:
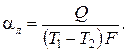 (2.30)
(2.30)
СЛОЖНЫЙ ТЕПЛООБМЕН
Как уже было сказано, разделение теплопереноса на теплопроводность, конвекцию и излучение удобно для изучения этих процессов.
Однако, очень часто встречается сложный теплообмен, при котором теплота передается двумя или всеми тремя способами одновременно. Например, теплоотдача от поверхности к газу (или от газа к поверхности). При этом имеет место как конвективный теплообмен между поверхностью и омывающим ее газом, так и излучение. В этом случае интенсивность теплообмена характеризуется суммарным коэффициентом теплоотдачи:
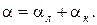 (2.31)
(2.31)
В ряде случаев влиянием одной из составляющих коэффициента теплоотдачи можно пренебречь. Например, с увеличением температуры резко возрастает тепловой поток излучения, поэтому при температуре выше 1000 °C обычно принимают 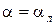 и наоборот, при теплообмене поверхности с потоком капельной жидкости определяющим является конвективный теплообмен, т. е.
и наоборот, при теплообмене поверхности с потоком капельной жидкости определяющим является конвективный теплообмен, т. е. 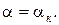
В практике пожарного дела в условиях пожара греющей средой являются продукты горения и коэффициент теплоотдачи a приближенно вычисляют по уравнению:
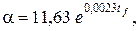 (2.32)
(2.32)
где 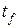 – температура греющей среды.
– температура греющей среды.
2.5. ТЕПЛОПЕРЕДАЧА МЕЖДУ
ДВУМЯ ЖИДКОСТЯМИ ЧЕРЕЗ СТЕНКУ
На практике часто приходится рассчитывать стационарный процесс переноса теплоты от одного теплоносителя к другому через разделяющую их стенку. Такой процесс называется теплопередачей. Он объединяет все рассмотренные нами элементарные процессы.
Вначале теплота передается от горячего теплоносителя 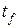 г к одной из поверхностей стенки путем конвективного теплообмена, который, как это было сказано ранее, может сопровождаться излучением. Интенсивность процесса теплоотдачи характеризуется коэффициентом теплоотдачи a1. Затем теплота теплопроводностью переносится от одной поверхности стенки к другой. Термическое сопротивление теплопроводности R рассчитывается по формулам (2.6) и (2.7) в зависимости от вида стенки. Далее теплота путем конвективного теплообмена, характеризуемого коэффициентом теплоотдачи a2, передается от поверхности стенки к холодной жид-
г к одной из поверхностей стенки путем конвективного теплообмена, который, как это было сказано ранее, может сопровождаться излучением. Интенсивность процесса теплоотдачи характеризуется коэффициентом теплоотдачи a1. Затем теплота теплопроводностью переносится от одной поверхности стенки к другой. Термическое сопротивление теплопроводности R рассчитывается по формулам (2.6) и (2.7) в зависимости от вида стенки. Далее теплота путем конвективного теплообмена, характеризуемого коэффициентом теплоотдачи a2, передается от поверхности стенки к холодной жид-
кости.
При стационарном режиме тепловой поток Q во всех трех процессах одинаков, а перепад температур между горячей и холодной жидкостями складывается из трех составляющих:
· между горячей жидкостью и поверхностью стенки:
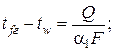 (2.33)
(2.33)
· между поверхностями стенки:
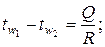 (2.34)
(2.34)
· между второй поверхностью стенки и холодной жидкостью:
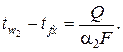 (2.35)
(2.35)
Из этих уравнений (2.33)-(2.35) получается формула
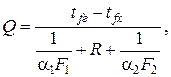 (2.36)
(2.36)
позволяющая рассчитывать процесс теплопередачи через любую стенку: плоскую, цилиндрическую, однослойную, многослойную и др., отличия при этом будут только в расчетных формулах R.
В случае теплопередачи через плоскую стенку, для которой 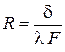 и площади поверхностей плоской стенки одинаковы с обеих сторон
и площади поверхностей плоской стенки одинаковы с обеих сторон 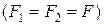 , удобнее рассчитывать плотность теплового потока q. Тогда уравнение (2.36) преобразуется к виду:
, удобнее рассчитывать плотность теплового потока q. Тогда уравнение (2.36) преобразуется к виду:
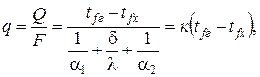 (2.37)
(2.37)
где 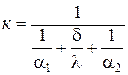 – коэффициент теплопередачи, (2.38)
– коэффициент теплопередачи, (2.38)
характеризующий интенсивность процесса теплопередачи от одного теплоносителя к другому через разделяющую их плоскую стенку.
Формулой (2.38) можно воспользоваться и при расчете теплового потока через тонкие цилиндрические стенки, если
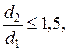 (2.39)
(2.39)
здесь d2 и d1 – внешний и внутренний диаметры цилиндрической стенки (трубы).
ЗАДАНИЕ № 3
Дата добавления: 2021-06-28; просмотров: 619;











