ЛИНЕЙНЫЕ ЗАДАЧИ ЦЕЛОЧИСЛЕННОГО

ПРОГРАММИРОВАНИЯ

В целочисленном программировании рассматриваются задачи, в которых на значения всех или части переменных наложено требование целочисленности. Наиболее изучены линейные задачи целочисленного программирования, которые записываются, например, в виде:

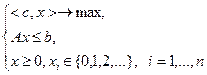(2.4.1)

Условия целочисленности, накладываемые на значения переменных в задачах рассматриваемого типа, в общем виде можно представить следующим образом:

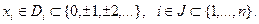(2.4.2)

Если в (2.4.2) 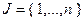, то на все переменные задачи наложено условие целочисленности. Именно такая ситуация имеет место в постановке задачи (2.4.1). Если, например, 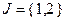, то ограничение целочисленности наложено только на значения двух переменных. В тех случаях, когда требование целочисленности наложено на значения только части переменных, соответствующие задачи целочисленного программирования называют смешанными задачами. Если в (2.4.2) 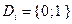, то при таких ограничениях задача целочисленного программирования называется задачей булева программирования.

Рассмотрим примеры практических задач, которые могут быть сформулированы в виде линейных задач целочисленного программирования.

Пример 2.4.1. Транспортная задача

Имеется 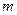баз для хранения товара и 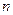пунктов потребления. Доставка единицы товара с 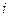-й базы до 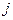-го пункта стоит 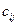. Известно также, что на 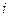-й

базе находится 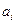единиц товара ( 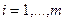) и что потребность 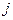-го пункта потребления составляет 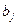единиц ( 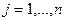). Требуется определить, сколько единиц товара следует направить с каждой из баз в каждый из пунктов потребления, чтобы обеспечить минимальную суммарную стоимость доставки.

Введем переменную 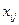, которая будет принимать значение количества единиц товара, направляемого с 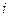-й базы в 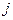-й пункт. Тогда задача запишется в виде:

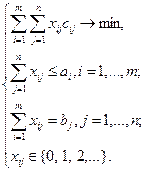
Пример 2.4.2. Задача об оптимальной загрузке (о рюкзаке)

Авиационная часть обладает запасом, состоящим из бомб 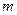типов в количестве 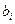штук по каждому типу ( 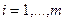). Имеются также бомбардировщики 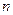видов в количестве 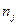самолетов по каждому виду ( 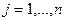). Для каждого из типов бомб известны эффективность 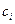и вес 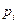( 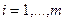), а для каждого из видов бомбардировщиков – грузоподъемность 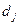( 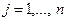). Требуется определить, сколько бомб каждого типа следует загрузить в бомбардировщик каждого вида с тем, чтобы обеспечить максимальную эффективность воздействия на противника.

Обозначим через 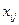количество бомб 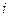-го типа, которое нужно загрузить в бомбардировщик 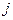-го вида. Тогда с учетом вышеизложенного задача формулируется следующим образом:

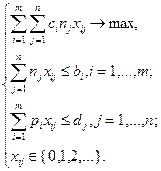
Пример 2.4.3. Задача о коммивояжере (о бродячем торговце)

Имеется 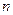городов и известна матрица [ 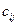] расстояний между этими городами. Коммивояжер должен проехать все города, побывав один раз в каждом городе и вернуться в исходный город. Требуется найти маршрут, обеспечивающий минимум пройденного расстояния.

Любой маршрут можно представить в виде перестановки из 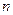номеров последовательно проезжаемых городов: 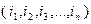. Всего имеется 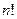таких перестановок. Каждой перестановке соответствует определенное расстояние, пройденное коммивояжером:

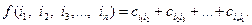
Решение задачи может быть найдено путем перебора возможных маршрутов. Однако с ростом числа городов число вариантов быстро достигает огромных значений, что вынуждает отказаться от прямого перебора. Данная задача сводится к линейной задаче целочисленного программирования введением дополнительной переменной

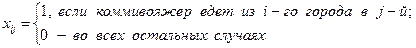
и записывается следующим образом:

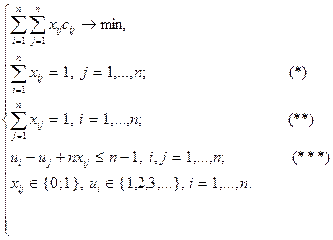
Ограничения 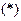являются условием, обеспечивающим выполнение требования, состоящего в том, что коммивояжер должен приезжать в каждый город только один раз, а ограничения 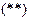– что он должен выезжать из каждого города только один раз. Ограничения 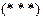отвечают за то, чтобы маршрут коммивояжера был односвязным, т.е. чтобы не было разрывов траектории; 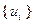– некоторые специально подобранные целые числа. Отметим, что в качестве элементов матрицы [ 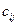] можно также рассматривать время, издержки или другой показатель.

Общие методы линейного программирования непосредственно к линейным задачам целочисленного программирования применять нельзя, так как в большинстве случаев они дают дробные решения. Округление получаемых при этом результатов до ближайших целых чисел может не только привести к отдалению от оптимального целочисленного решения, но и вывести за пределы допустимого множества задачи. Существует весьма узкий класс задач линейного программирования, среди оптимальных решений которых всегда имеется целочисленное. К этому классу относятся, например, транспортная задача, задача о кратчайшем пути и некоторые другие. Такие задачи можно решать обычными методами линейного программирования. Однако для решения многих других задач рассматриваемого типа разработаны специальные методы, к числу которых относятся методы отсечения и метод ветвей и границ.

Идея методов отсечения заключается в следующем. Сначала задача решается без учета ограничений целочисленности. Если полученное решение целочисленно, то оно является оптимальным решением задачи. В противном случае к условиям исходной задачи добавляется линейное ограничение, которому удовлетворяют все целочисленные решения исходной задачи, но не удовлетворяет полученное нецелочисленное решение. Такая процедура отсечения продолжается вплоть до получения на некотором шаге целочисленного оптимального решения либо до выявления неразрешимости задачи. Рассмотрим линейную задачу целочисленного программирования:

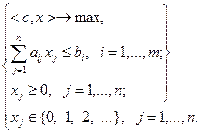(2.4.3)

Допустимое множество задачи (2.4.3) может быть записано в виде:

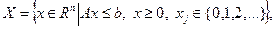(2.4.4)

где часть ограничений задачи (2.4.3) записана в компактной форме, подобно тому, как это было сделано в (2.4.1). Пусть 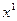– решение задачи, которой в (2.4.3) соответствуют строки, охваченные правой фигурной скобкой. Если 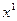удовлетворяет условию, записанному в (2.4.3) в последней строке, т.е. если найденное решение оказалось целочисленным, то оно является решением всей исходной задачи. Если 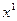не удовлетворяет условию целочисленности, то добавляется линейное ограничение:

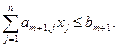(2.4.5)

Это ограничение является отсечением, так как оно формируется таким образом, что ему не удовлетворяет точка 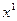, т.е. обеспечивается выполнение неравенства:

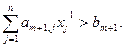(2.4.6)

При формировании ограничения (2.4.5) обеспечивается также его правильность. Требование правильности заключается в том, чтобы не было отсечено ни одной целочисленной допустимой точки, т.е. чтобы допустимое множество (2.4.4) удовлетворяло соотношению

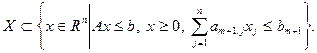(2.4.7)

В результате получаем задачу, подобную задаче, которая соответствует строкам, охваченным в (2.4.3) правой фигурной скобкой, однако в которой уже на одно ограничение больше. Затем решаем эту задачу и вновь проверяем полученное решение на целочисленность. Если оно удовлетворяет условию целочисленности, то принимается в качестве решения всей исходной задачи. В противном случае формируется очередное отсечение

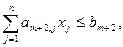
которое добавляется в качестве нового ограничения в исходную задачу. Описанный процесс продолжается вплоть до получения окончательного результата.

Среди методов отсечения наиболее известен метод Гомори, суть которого заключается в следующем. Рассмотрим каноническую задачу:

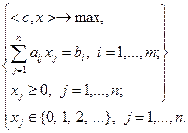(2.4.8)

Отбросив условие целочисленности, получим задачу, которая в (2.4.8) соответствует строкам, охваченным правой фигурной скобкой. Допустим, что с помощью симплекс-метода найдено решение этой задачи 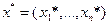– невырожденная опорная точка и что это решение не является целочисленным. Тогда среди значений координат точки 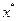имеется по крайней мере одно число с ненулевой дробной частью, т.е.

.

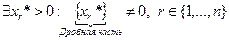Согласно (2.2.8), произвольный вектор-столбец матрицы 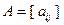в задаче (2.4.8), определяемый в соответствии с (2.2.3), может быть представлен в виде линейной формы относительно базисных векторов :

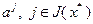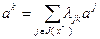, где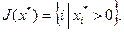

Используя коэффициенты этого разложения, построим отсечение:

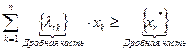(2.4.9)

Докажем, что данное выражение является правильным отсечением. Сначала покажем, что точка 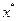не удовлетворяет неравенству (2.4.9). Если 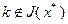, то, как известно, 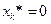. Поэтому

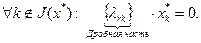
Если же 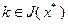, то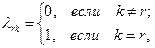

т.е. в этом случае дробные части коэффициентов 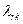равны нулю. Таким образом, используя координаты точки 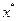, для суммы в левой части (2.4.9) можно записать:

.

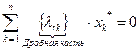Следовательно, выполнено неравенство

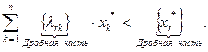
Полученный результат означает, что точка 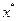ограничению (2.4.9) не удовлетворяет, т.е. оно действительно является отсечением.

Возьмем произвольную допустимую точку 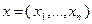рассматриваемой задачи (2.4.8), т.е. точку, удовлетворяющую всем ограничениям задачи, включая условие целочисленности. Будем также использовать точку 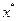, которая определена выше. Тогда можно записать:

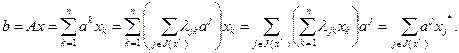(2.4.10)

Последнее равенство справедливо в силу того, что

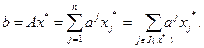
Здесь при записи ограничений задачи (2.4.8) использованы вектор 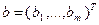и матрица 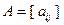. Поскольку векторы-столбцы 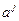матрицы 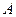при 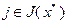образуют базис, а разложение по базису единственно, из (2.4.10) следует:

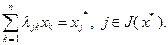(2.4.11)

В частности, при 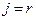(2.4.11) принимает вид:

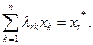(2.4.12)

Из полученного выражения следует справедливость неравенств:

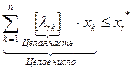
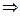
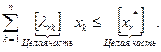(2.4.13)

Теперь выясним, удовлетворяет ли точка 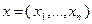ограничению (2.4.9). Для этого, используя полученные результаты, в частности соотношения (2.4.12) и (2.4.13), преобразуем, а затем оценим левую часть неравенства (2.4.9):

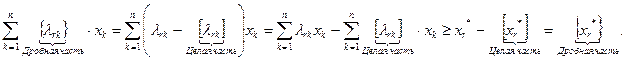
Итак, точка 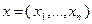удовлетворяет ограничению (2.4.9). С учетом этого и ранее полученных результатов можно утверждать, что выражение (2.4.9) является правильным отсечением.

Метод ветвей и границ по существу является методом частичного перебора, предназначенным для решения задач оптимизации с ограничениями, в котором осуществляется направленный поиск оптимального решения в пределах допустимого множества рассматриваемой задачи. Следует отметить, что метод ветвей и границ является одним из наиболее общих подходов к решению задач, для которых не разработаны эффективные регулярные методы. К таким задачам относятся задачи комбинаторного типа, нелинейного программирования (например, задачи максимизации невыпуклой функции), а также целочисленного программирования. В основе метода ветвей и границ лежат построения, которые обычно позволяют существенно уменьшить объем перебора:

а) вычисление верхней границы (для задачи максимизации); в этом случае исходная задача заменяется задачей, для решения которой существуют эффективные методы, причем значение максимизируемой функции в ней не меньше соответствующего значения целевой функции в исходной задаче;

б) разбиение на подмножества (ветвление); осуществляется постепенное разбиение допустимого множества исходной задачи на дерево подмножеств и последовательное уточнение значения верхней границы на каждом из этих подмножеств. Способы вычисления верхней границы и реализация процесса ветвления зависят от структуры конкретной задачи, ее специфических особенностей, учет которых приводит к различным реализациям схемы метода ветвей и границ.

Рассмотрим задачу на максимум в постановке (1.1)

, ,

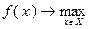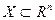которая не предполагает обязательную линейность целевой функции 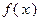и ограничений, определяющих допустимое множество 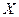задачи. Решение этой задачи методом ветвей и границ предполагает наличие возможности оценки произвольного подмножества 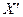множества 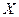. Иными словами, для 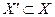необходимо уметь строить (или получать) такое число 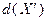, которое удовлетворяет выражению

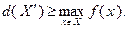
Величину 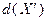называют оценкой максимума функции 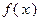на множестве 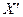. Одним из способов ее получения является использование расширения 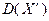подмножества 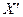. Тогда

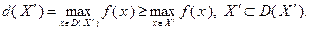
В результате получим оценку сверху значения максимума функции 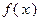на подмножестве 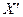или его границу. Кроме этого, необходимо уметь осуществлять ветвление, т.е. уметь разбивать произвольное подмножество 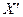множества 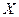на подмножества, которые не пересекаются. Если 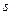– число таких непересекающихся подмножеств, то

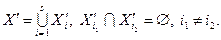
В процессе реализации метода ветвей и границ вычисляются значения так называемого рекорда 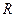. Вначале полагают 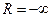. После получения первой допустимой точки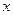 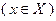значение рекорда становится равным 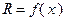. При этом фиксируется значение 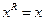. В дальнейшем в каждой новой полученной допустимой точке вычисляется значение целевой функции, которое сравнивается с текущим значением рекорда. В результате этого сравнения значение рекорда может быть обновлено. Это происходит в том случае, если в некоторой новой допустимой точке 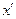значение 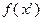оказывается больше текущего значения 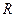. Тогда значение рекорда обновляется и становится равным 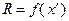. Соответственно фиксируется новое значение 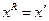. На каждом шаге работы метода ветвей и границ используется свой список (совокупность) подмножеств множества 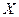. На первом шаге используется список 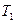, состоящий из самого множества 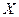: 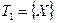; при этом 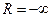. Допустим, что на втором шаге получено разбиение допустимого множества 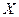задачи на три непересекающихся подмножества 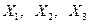и определены значения оценок 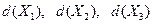путем использования расширений 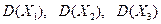подмножеств 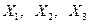. Если хотя бы одна из оценок оказалась вычисленной в допустимой точке, то изменится значение рекорда 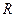. Если 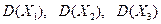не пусты и максимумы на них достигаются не в допустимых точках, то подмножества 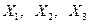надо ветвить (т.е. разбивать) дальше. Если для какого-либо из подмножеств, например для 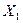, окажется выполненным неравенство 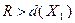, то подмножество 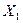исключается из дальнейшего рассмотрения, так как решение задачи ему не принадлежит. Если какое-либо из расширений 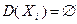, то 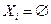, и в этом случае подмножество 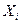также исключается из списка.

Допустим, что на 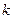-м шаге работы метода ветвей и границ получен список подмножеств

.

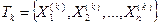Если какое-либо из этих подмножеств пусто, то оно исключается из дальнейшего рассмотрения. Для всех непустых подмножеств списка определяются значения оценок 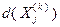. Среди этих значений могут оказаться значения оценок, полученные в точках, принадлежащих допустимому множеству задачи. Если таковые имеются и наибольшее из них превышает текущее значение рекорда 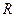, то текущее значение рекорда обновляется и становится равным этому наибольшему значению оценки величины максимума. При этом работа с подмножеством, на котором получено наибольшее значение оценки, завершается. В случае, если 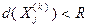, подмножество 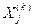исключается из дальнейшего рассмотрения. Если 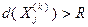и оценка максимума 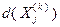получена в точке, не принадлежащей допустимому множеству задачи, процесс ветвления должен быть продолжен.

На рис. 2.4.1 приведен пример схемы решения оптимизационной задачи методом ветвей и границ. На первом шаге работы имеем список 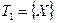, состоящий из допустимого множества 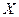задачи, и значение рекорда 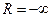. На втором шаге сформирован список подмножеств 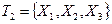. При этом выполнены неравенства 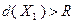и 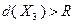, причем значения оценок 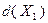и 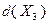получены в точках, не принадлежащих допустимому множеству задачи. Следовательно, подмножества 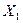и 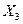подлежат дальнейшему разбиению. Подмножество 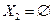исключается из списка. На третьем шаге работы получен

Рис. 2.4.1. Схема решения задачи методом ветвей и границ

список 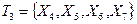. При этом 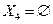исключается из списка. Значения оценок 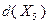и 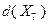получены в точках, принадлежащих допустимому множеству задачи, и превышают текущее значение рекорда, поэтому рекорд подлежит обновлению: 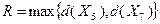. Поскольку оказалось выполненным неравенство 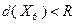, подмножество 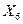исключается из списка. Решением данной задачи является точка, принадлежащая объединению подмножеств 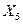и 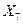, в которой получено наибольшее из значений оценок максимума 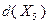и .

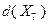Рассмотрим линейную задачу целочисленного программирования (2.4.1):

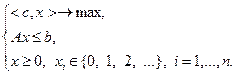
Допустимое множество этой задачи

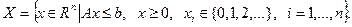
Решая задачу (2.4.1) методом ветвей и границ, на первом шаге работы имеем список 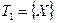и значение рекорда 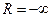. Находим оценку сверху максимума целевой функции задачи, используя расширение допустимого множества

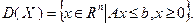
Для этого необходимо решить задачу

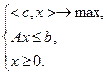(2.4.14)

Если решение этой задачи, полученное, например, симплекс-методом, оказалось принадлежащим множеству 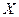, т.е. целочисленным, то исходная задача решена. В противном случае в решении задачи (2.4.14) имеется координата, не являющаяся целым числом. Обозначим ее 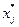и выполним ветвление путем разбиения множества 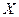на два подмножества 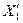и :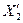

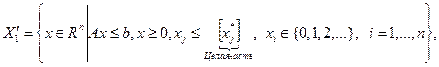
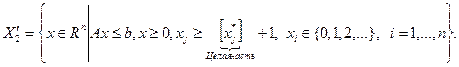
Очевидно, что 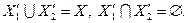Продолжение решения данной задачи осуществляется в соответствии с приведенным выше описанием метода ветвей и границ. Проиллюстрируем применение рассматриваемого метода на следующем примере решения линейной задачи целочисленного программирования.

Пример 2.4.4

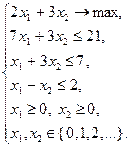(2.4.15)

Отбросив условие целочисленности, записанное в последней строке (2.4.15), получим стандартную задачу линейного программирования, допустимое множество которой является расширением 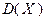допустимого множества 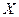исходной задачи. Графическое решение этой стандартной задачи представлено на рис. 2.4.2. Перемещая прямую, ортогональную вектору с координатами 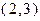параллельно самой себе в направлении этого вектора, получаем решение в точке пересечения прямых 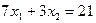и 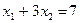: 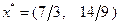. Крайнее положение перемещаемой прямой соответствует прямой 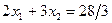, показанной на рисунке. Подстановка найденного решения в целевую функцию дает

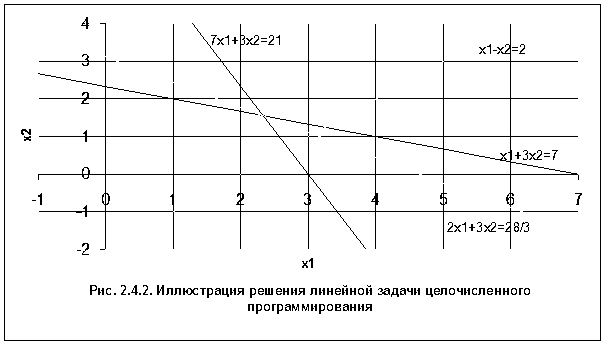
значение оценки сверху ее максимума для исходной задачи: 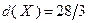. На рассматриваемом первом шаге решения задачи имеем список 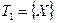и значение рекорда 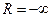. Далее осуществляем разбиение множества 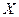на два подмножества 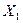и :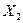

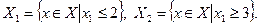
Таким образом, 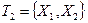. Поскольку 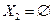, исключаем это подмножество из списка и продолжаем решение на подмножестве 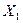. Отбросив в опреде-

лении подмножества 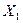условие целочисленности, получим расширение этого подмножества 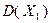. Графическое решение стандартной задачи линейного программирования с целевой функцией, представленной в (2.4.15), и допустимым множеством 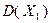приводит к получению результата в точке пересечения прямых 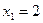и 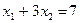, т.е. в точке 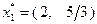. Подстановка найденного решения в целевую функцию дает значение оценки сверху ее максимума для исходной задачи: 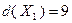. На следующем шаге разбиваем подмножество 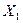на два подмножества 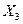и :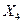

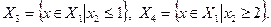
В результате имеем список 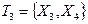. Отбросив в определении подмножества 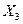условие целочисленности, получим расширение этого подмножества 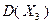. Графическое решение задачи, полученной из (2.4.15) заменой ее допустимого множества множеством 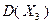, дает результат 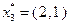. Подставив найденное решение в целевую функцию, находим 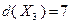. Теперь рассмотрим подмножество 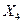. Исключив из его определения условие целочисленности, получим расширение данного подмножества 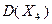. Графическое решение задачи линейного программирования с целевой функцией, представленной в (2.4.15) и допустимым множеством 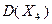приводит к результату 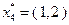. Подстановка полученного решения в целевую функцию позволяет определить 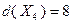. Таким образом, 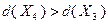и, следовательно, 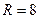, а точка 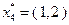является решением исходной задачи.